程序员的数学之余数II

乘方的尾巴

按照之前求余数的那种规律，该怎么求的最后一个数呢？

- 的结果是`1`，个位数是`1`

- 的结果是`123456789`，的个位数是`9`

- 的结果是`15241578750190521`，的个位数是`1`

- 的结果是`1881676371789154860897069`，的个位数是`9`

- 的结果是`232305722798259244150093798251441`，的个位数是`1`

- 的结果是`28679718602997181072337614380936720482949`，的个位数是`9`

- ......

现在应该看出规律了吧：偶数次方时个位数是`1`，奇数次方时个位数是`9`。

由于计算值太大，不得已找了目前对大数计算比较友好的语言Groovy。

这是Groovy可以得到的计算结果：5816245886......（后面有19万位）

黑白棋通信

一位魔术表演者的面前有七枚随机摆放的黑白棋（有的黑面在上，有的白面在上）。

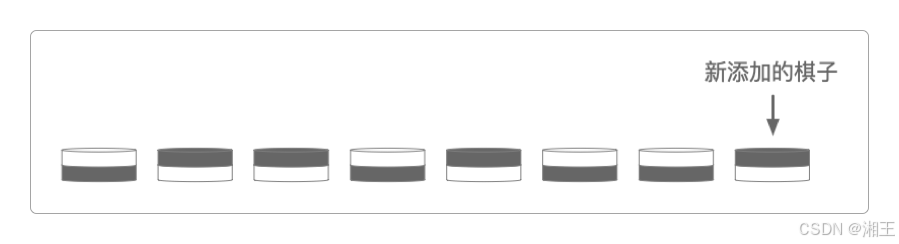
魔术师看完棋子的摆放后就蒙上眼睛，他的徒弟又往里面添加了一枚棋子。

这时观众可以将其中的一枚棋子翻面，或不翻转任何棋子（一次最多只能翻一枚）。

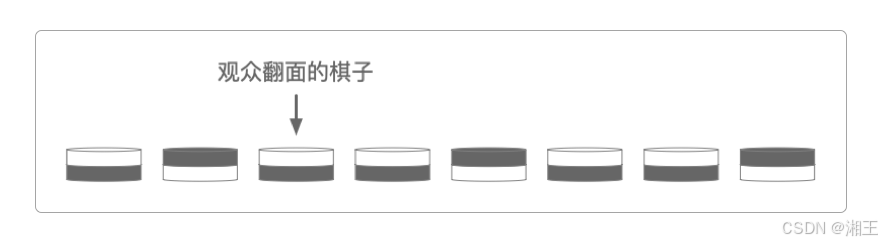
观众翻面时，没有人说话或发出响声，所以魔术师是不知道观众有没有翻棋的。

当魔术师摘下眼罩，观察8枚棋子之后，就能马上知道“观众翻转了棋子”，或者“观众没有翻转棋子”。

这是怎么做到的呢？

其实答案就出在徒弟添加的那枚棋子上。

- 在魔术师蒙上眼睛之前，可以知道黑棋的个数是奇数还是偶数。

- 假设徒弟和魔术师约定：添加的棋子，必须让黑棋的个数是偶数。

- 那么观众的行为就可以造成下面三种结果。

- 观众翻转黑棋，那么黑棋的个数就变成了奇数。

- 观众翻转白棋，那么黑棋的个数也还会是奇数。

- 观众什么也不做，那么黑棋的个数还是偶数。

这就是魔术师可以很快判定观众行为的原因。

这其实就是网络上数据传输的奇偶校验规则：徒弟是发送方，魔术师是接收方，而观众则是`干扰信号的噪声`。

不过，可以很明显地看出这种检验方式的缺陷：如果观众动了2个或2个以上的棋子，就不好判断了。