ISTFT和STFT是否可逆的问题

引言：

前几天听了汪德亮老师的讲座，碰到一个奇怪的问题：在低信噪比、高混响下对原始信号时频幅度谱进行修正后，再进行$istft$和$stft$的转换，此时的时频谱和修正后的原始时频谱不一样，而且 $istft$后获得的时域信号并没有起到去混响的效果反而是十分奇怪的声音。当时同事们对此现象都感到疑惑。按照我的理解，对于任意的复数域元素$H$,$H\in C^{MN}$,$M$表示数据的帧数,$N$表示数据的频点数，存在如下的关系：$stft(istft(H))=H$,如果以上的关系不成立，则现在绝大多数的音频增强算法的套路：对幅度谱进行修正，利用带噪信号相位谱进行istft变换获得修正时域语音，会存在一定的风险。下面对这一问题进行讲解。

代码：

realData = rand(257,100);
%realData = [realData;realData(end-1:-1:2,:)];
imgData = rand(257,100);
%imgData = [imgData;-imgData(end-1:-1:2,:)];
comData = realData + 1i*imgData;
overLap = 0.5;
frameSize = 512;
y = ISTFT(comData, frameSize, overLap);
[ftbin,Nframe,Nbin,Lspeech,speechFrame] = STFT((y), frameSize, overLap, frameSize);
error = squeeze(ftbin) - comData ;

data = ones(10240,1);
overLap =0.5;
[ftbin1,Nframe,Nbin,Lspeech,speechFrame]= STFT(data, frameSize, overLap, frameSize);
y1 = ISTFT(squeeze(ftbin1), frameSize, overLap);
[ftbin2,Nframe,Nbin,Lspeech,speechFrame]= STFT(y1, frameSize, overLap, frameSize);
error1 = data - y1;
error2 = squeeze(ftbin1) - squeeze(ftbin2) ;

$H\in C^{MN}$:任意的复数矩阵
$F$:运算符
$H$:运算符

$$F(H) = G(H) - H$$
$$G(H) = STFT(iSTFT(H ))$$

按照一般的理解，$F(H)=0$成立，然而根据前文的介绍，该等式并非恒成立。

直接粘贴论文的定义吧：
The set of ==consistent spectrograms== can thus be described as the kernel (or null space) of the R-linear operator from
$C^{MN}$ to itself defined by

$$F(H) = G(H) - H$$

$$G(H) = STFT(iSTFT(H))$$

Let $H(m,n)$be a set of complex numbers, where $m$ will correspond to the frame index and $n$ to the frequency band index, and $W$and $S$ be analysis and synthesis
windows verifying the perfect reconstruction conditions for
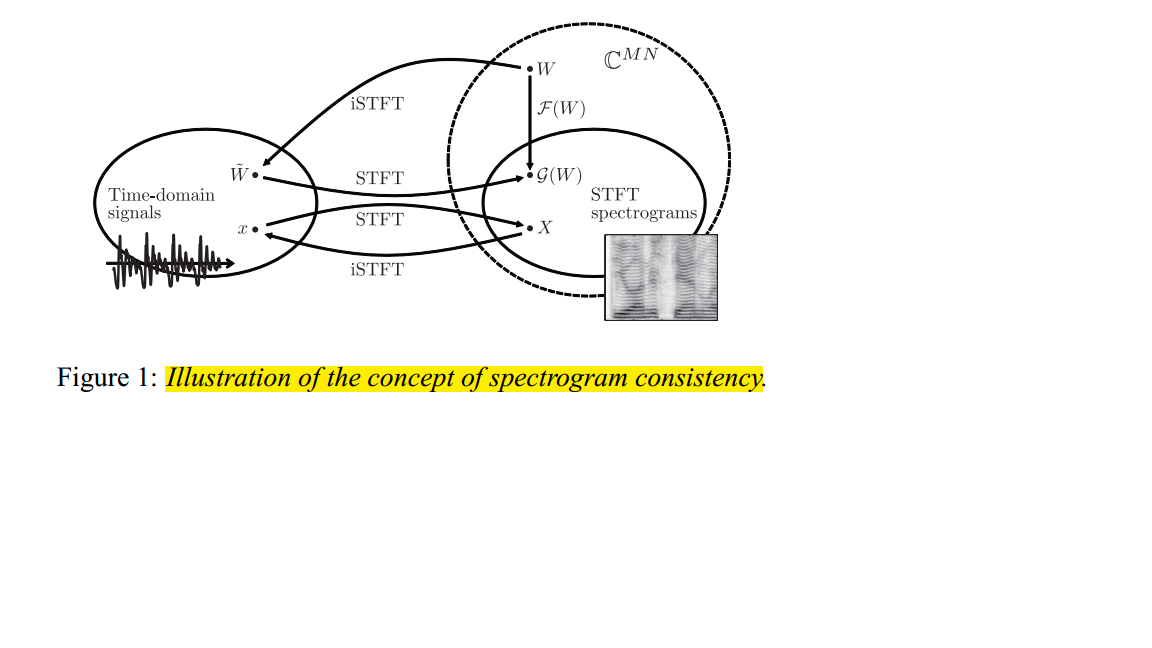
a frame shift $S$. For the set $H$ to be a consistent STFT spectrogram, it needs to be the $STFT$ spectrogram of a signal $X(t)$. But by consistency, this signal can be none other than the result of the inverse STFT of the set $H(m,n)$. A necessary and sufficient condition for $H$ to be a consistent spectrogram is thus for it to be equal to the $STFT$ of its inverse $STFT$. The point here is that, for a given window length $N$ and a given frame shift, if we denote the inverse $STFT$ by $iSTFT$, the operation $iSTFT – STFT$ from the space of real signals to itself is the identity, while $STFT – iSTFT$ from $C^{MN}$ to itself is not.

这个问题对我们的启示是，在进行语音增强后通过得到的频域幅度谱恢复出的时域信号再返回到时谱幅度谱时两者并不相同，前端信号处理在频域完成处理后输出时域信号给识别器时，其提取的MFCC特征可能并不是最优的。对于该问题更严格的推导，可参考论文。

参考论文：

1.Explicit consistency constraints for STFT spectrograms and their application to phase reconstruction.
2.FAST SIGNAL RECONSTRUCTION FROM MAGNITUDE STFT SPECTROGRAM
BASED ON SPECTROGRAM CONSISTENCY.

author:longtaochen
email:1440935236@qq.com