解读神经网络可解释性：梯度视角下的卷积操作解析-优快云博客

本文探讨了如何通过计算梯度理解卷积神经网络的工作原理，以GradCAM为例，详细剖析了特征图对输出的影响。通过链式法则，逐步揭示了从特征图到输出的数学过程，并提供了相关代码演示。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

在一些对神经网络可解释性的研究中，总是会利用到损失函数对最后一层特征图进行求梯度的操作，例如著名的Grad CAM，因此对于卷积神经网络的理解不能仅仅停留在调包的阶段，我们需要拆解开它求梯度的黑盒。
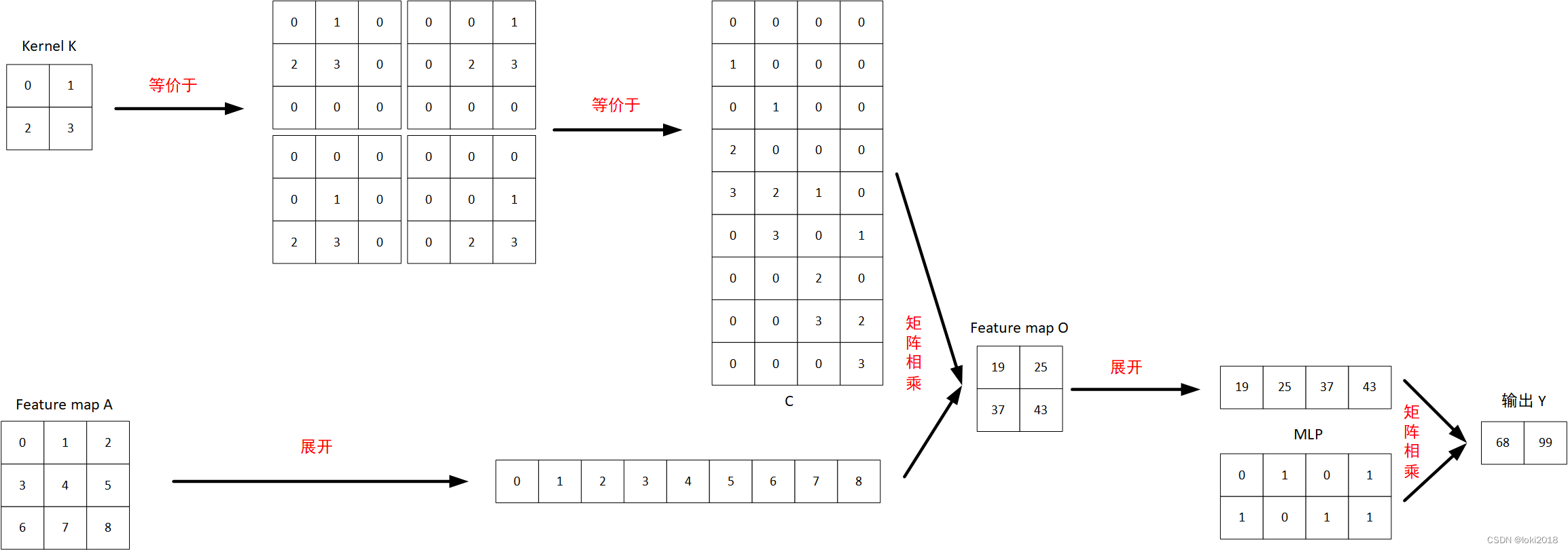
在这里插入图片描述

如图所示，假设有一个特征图 $A$ , 经过一个 $\times 2$ 的卷积核 $K$ 操作之后，得到一个新的特征图 $O$ ,再将其展平后经过 $M L P$ 得到一个长度为2的输出向量 $Y$ 。
如果想要知道特征图 $A$ 的每个元素对最终输出的贡献大小，就需要计算出 $Y$ 对 $A$ 中每个元素的偏导，即 $∂Y∂A\frac{ \partial Y }{ \partial A }$ 。
我们整理一下从特征图 $A$ 得到输出 $Y$ 的过程，可以写为：
$O = C O N V (A)$
$Y = M L P (O)$
因此根据链式求导法则， $∂Y∂A=∂Y∂O∂O∂A\frac{ \partial Y }{ \partial A }= \frac{ \partial Y }{ \partial O} \frac{ \partial O }{ \partial A}$ 。
以输出 $Y_1=68$ 为例， $Y_1=0*O_{11}+1*O_{12}+0*O_{21}+1*O_{22}$ , 因此 $∂Y1∂O=[0101]\frac{ \partial Y_1 }{ \partial O }=[0 \quad1 \quad0\quad1]$
再来计算 $∂O∂A=[∂O11∂A11∂O11∂A12∂O11∂A13∂O11∂A21…∂O11∂A33∂O12∂A11∂O12∂A12∂O12∂A13∂O12∂A21…∂O12∂A33∂O21∂A11∂O21∂A12∂O21∂A13∂O21∂A21…∂O21∂A33∂O22∂A11∂O22∂A12∂O22∂A13∂O22∂A21…∂O22∂A33]=CT\frac{ \partial O }{ \partial A}=\begin{bmatrix} \frac{ \partial O_{11} }{ \partial A_{11}} & \frac{ \partial O_{11} }{ \partial A_{12}} & \frac{ \partial O_{11} }{ \partial A_{13}} & \frac{ \partial O_{11} }{ \partial A_{21}} & \dots & \frac{ \partial O_{11} }{ \partial A_{33}} \\ \frac{ \partial O_{12} }{ \partial A_{11}} & \frac{ \partial O_{12} }{ \partial A_{12}} & \frac{ \partial O_{12} }{ \partial A_{13}} & \frac{ \partial O_{12} }{ \partial A_{21}} & \dots & \frac{ \partial O_{12} }{ \partial A_{33}} \\ \frac{ \partial O_{21} }{ \partial A_{11}} & \frac{ \partial O_{21} }{ \partial A_{12}} & \frac{ \partial O_{21} }{ \partial A_{13}} & \frac{ \partial O_{21} }{ \partial A_{21}} & \dots & \frac{ \partial O_{21} }{ \partial A_{33}} \\ \frac{ \partial O_{22} }{ \partial A_{11}} & \frac{ \partial O_{22} }{ \partial A_{12}} & \frac{ \partial O_{22} }{ \partial A_{13}} & \frac{ \partial O_{22} }{ \partial A_{21}} & \dots & \frac{ \partial O_{22} }{ \partial A_{33}}\end{bmatrix} =C^T$
最后将结果整合之后，再将形状变换与 $A$ 相同即可，即 $[001024023]\begin{bmatrix} 0 & 0 & 1\\ 0 & 2 & 4 \\ 0 & 2 & 3\end{bmatrix}$ 。
以下是以上计算过程的代码，可以发现计算结果和推导是一致的。

import torch
import torch.nn as nn

X = torch.tensor([[0, 1, 2],
                  [3, 4, 5],
                  [6, 7, 8]]).reshape(1, 1, 3, 3).float()
X.requires_grad = True
kernel = torch.tensor([[0, 1],
                       [2, 3]]).reshape(1, 1, 2, 2).float()
conv = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=2, bias=False)
conv.weight.data = kernel

fc = nn.Linear(in_features=4, out_features=2, bias=False)
fc.weight.data = torch.tensor([[0, 1, 0, 1],
                               [1, 0, 1, 1]]).float()
print(conv(X))
O = fc(torch.flatten(conv(X), start_dim=1))
print(O)

O[0][0].backward()

print(X.grad)

卷积神经网络的梯度求解