【算法】摘花生（动态规划）

题目

Hello Kitty想摘点花生送给她喜欢的米老鼠。

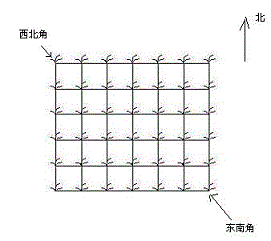
她来到一片有网格状道路的矩形花生地(如下图)，从西北角进去，东南角出来。

地里每个道路的交叉点上都有种着一株花生苗，上面有若干颗花生，经过一株花生苗就能摘走该它上面所有的花生。

Hello Kitty只能向东或向南走，不能向西或向北走。

问Hello Kitty最多能够摘到多少颗花生。

输入格式

第一行是一个整数T，代表一共有多少组数据。

接下来是T组数据。

每组数据的第一行是两个整数，分别代表花生苗的行数R和列数 C。

每组数据的接下来R行数据，从北向南依次描述每行花生苗的情况。每行数据有C个整数，按从西向东的顺序描述了该行每株花生苗上的花生数目M。

输出格式

对每组输入数据，输出一行，内容为Hello Kitty能摘到得最多的花生颗数。

数据范围

1≤T≤100
1≤R,C≤100
0≤M≤1000

输入样例：

2
2 2
1 1
3 4
2 3
2 3 4
1 6 5

输出样例：

8
16

思路

Hello Kitty所到的每个点都是从前一个点向下或向右到达（假设(1,1)点是从（1,0）与（0,1）点到达的）

因此我们可以保留这两种走法的最大值。

例如点(i，j)的最大值是（i - 1，j）与（i，j - 1）中的较大值加上（i，j）的值。

图解如下：

状态转移方程如下

ans[i][j] = max(ans[ i ][ j  - 1 ] + x[ i ][ j ]  ,  ans[i - 1][j] + x[i][j]);

代码

#include<bits/stdc++.h>
using namespace std;
const int N = 110;
int n,m;
int x[N][N];
int ans[N][N];

void solve()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++)
            cin >> x[i][j];
    
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++)
            ans[i][j] = max(ans[i][j - 1] + x[i][j],ans[i - 1][j] + x[i][j]);
    cout << ans[n][m] << endl;
}

int main()
{
    int t;
    cin >> t;
    while(t --)
    {
        memset(ans,0,sizeof ans);
        solve();
    }

    return 0;
}

难度：简单

时/空限制：1s / 64MB

总通过数：42784

总尝试数：52464

来源：《信息学奥赛一本通》

算法标签 DP  线性DP

题目来自： 1015. 摘花生 - AcWing题库