基于AImin的流密码攻击

一种针对带有非线性滤波的基于LFSR的流密码的猜测然后代数攻击

摘要

本文引入了一个称为一阶最小代数免疫度 AImin(f) 的新参数，并研究了AImin(f)的一些理论性质。基于我们的研究成果，我们提出了一种针对具有非线性滤波布尔函数 f的基于线性反馈移位寄存器的流密码的猜测然后代数攻击。我们的方法利用 AImin(f)的性质采用了一种特定的猜测策略，并充分利用每一个已猜测的比特，尽可能多地生成次数为 AImin(f)的方程。在某些条件下，该方法的时间和数据开销低于传统代数攻击。我们的攻击表明， AImin(f)不应过小，这为滤波布尔函数 f提出了一个新的设计准则。我们将我们的方法应用于一个使用最大代数免疫布尔函数 f作为其滤波器的80级密钥流生成器，而 AImin(f)非常小，违反了我们的准则。传统代数攻击的时间复杂度和数据复杂度分别为 O(2^73.56)和 O(2^24.52)，内存开销为 O(2^49)。我们方法的时间复杂度和数据复杂度分别为 O(2^56.86) 和 O(2^5.36)，内存开销为 O(2^10.72)。

关键词 ：代数攻击 · Algebraic免疫性 · Guess-then-algebraic攻击 · LFSR-based流密码 · 1-st最小代数免疫性

1 引言

基于线性反馈移位寄存器的流密码在使用非线性滤波生成器或组合生成器方面的研究催生了许多分析方法和理论研究。其中最重要的密码分析工具是代数攻击。

库鲁瓦，N.T. 和 迈尔，W. 提出了针对具有线性反馈的流密码的代数攻击，该方法在 2003[3],中被提出，是面向基于LFSR的流密码的一种经典且高效的分析方法。代数攻击的基本思想分为三个步骤：

步骤1：利用密钥流位，构建一个以密钥位或初始向量值为变量的非线性方程组 A。

步骤2：将一个低次数的非零函数 g乘以方程组的每个方程，得到一个次数低于 A的方程组 B。

步骤3：求解方程组 B

自从提出代数攻击以来，涌现出许多与之相关的研究课题。学者们试图探索步骤2中非零函数 g的性质，从而形成了布尔函数的代数免疫性和零化子的研究领域 [1,2,4,6,8,10,12,13,15,16]。记 AN(f)={g ∈ Bn|f · g= 0}。任何函数 g ∈ AN(f) 称为 f的零化子。布尔函数 f的代数免疫性，记作 AI(f)，是指 f或 f+ 1[11]的非零零化子的最小代数次数，用于衡量布尔函数抵抗代数攻击的能力。n变量布尔函数的最大代数免疫性为 n‐变量布尔函数是 ⌊n/2⌋[3]，具有最大代数免疫性的布尔函数称为最大代数免疫布尔函数。

在本文中，对于一个布尔函数 f ∈ Bn（其中 Bn 是 n 变量布尔环），我们引入了一个称为 1 阶最小代数免疫度的参数 AImin(f)。我们证明了当 AI(f) 为最优时， AImin(f) ≤ AI(f)；特别地，当 n 为奇数时， AImin(f) < AI(f)。同时给出了一个简单的算法来计算 AImin(f)。

当基于线性反馈移位寄存器的流密码的滤波器是一个最大代数免疫布尔函数 f 时，其在最大程度上能够抵抗代数攻击。基于我们与 AImin(f) 相关的理论结果，我们提出了一种针对此类基于LFSR的流密码的猜测然后代数攻击。在猜测‐确定攻击中，猜测策略至关重要。我们的方法利用 AImin(f) 的性质，采用了一种特定的猜测策略。首先，我们猜测一些初始状态比特，其位置由 LFSR的具体结构以及 AImin(f) 的性质决定。在猜测了足够多的LFSR状态比特之后，我们充分利用LFSR的具体结构和滤波器抽头，尽可能多地推导出次数为 AImin(f) 的方程，然后求解所得到的方程组。

我们的方法具有三个特殊的优点。(a) 它充分利用每一个已猜测的比特，尽可能多地推导出次数为 AImin(f)的方程。事实上，在大多数情况下， AImin(f) 严格小于 AI(f)。(b) 它不仅利用了 f的性质，还利用了抽头位置，这有助于推导出尽可能多的信息。在某些条件下，其时间和数据开销小于[3]中给出的传统代数攻击。(c) 我们的攻击表明，滤波布尔函数f的设计应满足 AImin(f)不应过小，这是一个新的设计准则。

此外，我们将我们的方法应用于一个80级密钥流生成器。其滤波生成器是一个9变量的MAI布尔函数 f，而 AImin(f)非常小，这违反了我们的设计准则。该模型在最大程度上能够抵抗文献[3]中给出的传统代数攻击。传统代数攻击的时间和数据复杂度分别为 O(2^73.56)和 O(2^24.52)，内存开销为 O(2^49)。而我们方法的时间和数据复杂度分别为 O(2^56.86)和 O(2^5.36)，内存开销为 O(2^10.72)。

请注意，德布雷兹，B. 和 古宾，L. 在 [7] 中提出了一种针对具有低汉明重量反馈多项式的自缩生成器（SSG）的猜测‐判定代数攻击。该方法主要旨在分析自缩生成器，而我们的方法则针对具有最优代数免疫性的滤波布尔函数的基于线性反馈移位寄存器的流密码。他们首先猜测一些信息，然后建立一组多项式方程，并使用SAT求解算法MiniSAT求解该方程组。而我们的方法通过利用 AImin(f) 的理论性质来关注已猜测比特的位置，这是流密码学术领域的一个新参数。此外，在猜测部分状态比特后所导出的方程的次数为AImin(f)，这也是我们的方法与 [7] 中提出的猜测‐判定代数攻击之间最显著的区别。

本文组织如下：第2节介绍与我们工作相关的一些基础知识。在第3节中，我们引入一个称为1阶最小代数免疫性 AImin(f)的新参数，并进行了一些理论分析。我们还给出了计算 AImin(f)的一个简单算法。在第4节中，针对具有非线性滤波布尔函数的基于LFSR的密钥流生成器，我们提出了一种利用 AImin(f)的猜测‐代数攻击方法，并给出了一些基于LFSR的密钥流生成器的设计准则。在第5节中，我们将我们的方法应用于一个不满足我们准则的密钥流生成器。第6节总结了本文。

2 预备知识

库鲁瓦，N.T. 和 迈尔,W. 提出了对具有线性反馈的流密码的代数攻击[3]。他们主要关注具有非线性滤波布尔函数的基于LFSR的密钥流生成器。图1显示了通用模型。

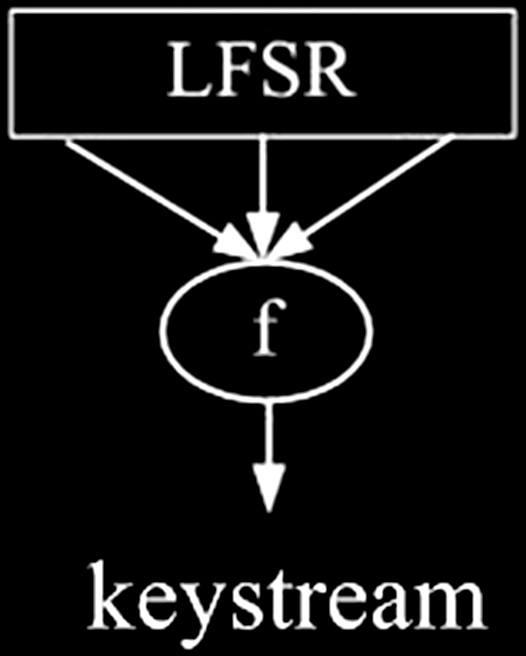
首先，我们对该模型进行简要描述。设线性反馈移位寄存器的长度为 l。L是LFSR的“连接函数”，且它是线性的。设LFSR的初始状态为 s0=(s0, s1,…, sl−1)，则它生成一个 m‐序列 s0, s1, s2…。为了叙述方便，我们将此 m‐序列称为LFSR序列。时刻t时LFSR的状态是
s_t=(st , st+1,…, st+l−1)= L^t (s0, s1,…, sl−1),

表1展示了在图1所示模型上，针对[3]的传统代数攻击（AA）的复杂度，其中M=( l AI(f))，且 ω为高斯消元的参数，在理论上为 ω ≤ 2.376[5]。

复杂度类型	数据复杂度	内存复杂度	时间复杂度
传统代数攻击（AA）	O(M)	O(M²)	O(M^ω)

该状态通过一个平衡非线性布尔函数 f ∈ Bn进行滤波。滤波生成器在时刻 t输出一位 ct。对于每个 ct，我们可以构造一个以若干密钥比特和初始值作为变量的方程。用 c0, c1, c2,…表示滤波生成器的输出，其中 ci ∈ F₂，则我们可以得到如下方程组：

$$
\begin{cases}
c_0 = f(s_0, s_1, …, s_{l-1}) \
c_1 = f(L(s_0, s_1, …, s_{l-1})) \
c_2 = f(L^2(s_0, s_1, …, s_{l-1})) \
\vdots
\end{cases}
$$

恢复 l线性反馈移位寄存器的初始状态比特的问题可归结为求解方程组(1)。

尽管正如[3]的作者所声明的那样，该算法中（被忽略的）常数因子预计会非常大，他们认为斯特拉森算法[14]是最快的实用算法。然后他们评估高斯约简的复杂度为 7 · M^(log₇2)/64 CPU时钟周期。为了方便起见，学者们通常使用表1中的 ω= 3来估计传统代数攻击的时间和数据复杂度。

我们可以得到，针对图1中所示模型的传统代数攻击的复杂度由 l和 AI(f)决定。当使用[3],中给出的传统代数攻击方法对每个密钥流比特进行攻击时，分析人员能够获得的方程的最低次数为 AI(f)。在下一节中，我们将尝试寻找一种方法，通过进一步探索非线性滤波函数的性质以及滤波抽头位置的结构，来判断是否可以降低时间和数据复杂度。

3 一阶最小代数免疫度 AImin(f)

在本节中，对于一个布尔函数 f(x₁, x₂, …, xₙ) ∈ Bₙ，我们给出一个称为1‐阶最小代数免疫性 AImin(f) 的新定义。首先，我们给出以下定义。

定义1

给定一个布尔函数 f(x₁, x₂, …, xₙ) ∈ Bₙ，对于某些固定的i, i ∈[1, n]，定义
AI(f|xᵢ=0) = AI(f(x₁, x₂, …, xᵢ₋₁, 0, xᵢ₊₁, …, xₙ)).
AI(f|xᵢ=1) = AI(f(x₁, x₂, …, xᵢ₋₁, 1, xᵢ₊₁, …, xₙ)).

定义2

给定一个布尔函数 f(x₁, x₂, …, xₙ) ∈ Bₙ，对于某些固定的i, i ∈[1, n]，定义
AIᵢ(f) = max{AI(f|xᵢ=0), AI(f|xᵢ=1)}.

定义3

对于一个布尔函数 f(x₁, x₂, …, xₙ) ∈ Bₙ，定义 f的一阶最小代数免疫度为
AImin(f) = min{AIᵢ(f): i ∈[1, n]}.

同时也定义
NAImin(f) = #{i|AIᵢ(f)= AImin(f): i ∈[1, n]},
其中“#”表示一个集合中元素的个数。

令 G={g ∈ AN(f|xᵢ=c)|deg(g)= AImin(f)}，同时也记作 nᵢ,𝒸 = #G，其中 𝒸 ∈{0, 1}。

基于上述定义，我们推导出定理1：

定理1

对于一个布尔函数 f(x₁, x₂, …, xₙ) ∈ Bₙ，如果其代数免疫性是最优的，则
AImin(f) ≤ AI(f).
特别地，如果 n为奇数，则
AImin(f) < AI(f).

证明 。给定 f(x₁, x₂, …, xₙ) ∈ Bₙ，可以表示为：
f(x₁, x₂, …, xₙ) = xᵢf₁(x₁, …, xᵢ₋₁, xᵢ₊₁, …, xₙ) + f₂(x₁, …, xᵢ₋₁, xᵢ₊₁, …, xₙ).
当 xᵢ固定时，只剩下 n −1个变量，根据定义1–3，可得
AImin(f) ≤ AIᵢ(f) ≤ ⌊(n−1)/2⌋ ≤ AI(f).
特别地，如果 n为奇数，则
AImin(f) ≤ AIᵢ(f) ≤ ⌊(n−1)/2⌋ < ⌊n/2⌋ = AI(f).

以下例子验证了定理1。

例子1

该布尔函数 f = x₁x₂x₃x₅ + x₁x₂x₅ + x₁x₂ + x₁x₃x₄x₅ + x₁x₃x₄ + x₁x₃x₅ + x₁x₄x₅ + x₁x₄ + x₂x₃ + x₂x₄x₅ + x₂x₅ + x₃x₄ + x₄x₅ + 1 是一个5变量 Carlet‐Feng布尔函数。我们可以得到 AI(f)= 3，这是最优的。 AIᵢ(f) i ∈[1, 5]的 f如表 2 所示。

xᵢ	x₁	x₂	x₃	x₄	x₅
AIᵢ(f)	2	2	2	2	2

我们可以看出 AImin(f) = AIᵢ(f) = 2 < AI(f) = 3, NAImin(f) = 5 > 1。

事实上，对于一个布尔函数 h ∈ Bₙ，尽管 AI(h)不是最大值，但有可能 AImin(h)严格小于 AI(h)。例如，对于流密码LILI‐128[9]所采用的滤波器函数 fd，有 AImin(fd) = 3 < AI(fd) = 4， NAImin(fd) = 4。

算法1展示了如何计算布尔函数 AImin(f) 和 NAImin(f)。

算法1：计算 AImin(f) 和 NAImin(f)

输入 ： I={1, 2,…, n}，布尔函数 f ∈ Bₙ。
设置 F= ∅、 E= ∅、 c ∈{0, 1}。
对于 i ∈ I 执行
计算定义2中定义的所有 AIᵢ(f)以及相应的nᵢ,𝒸
如果 AIᵢ(f) ≤ AI(f) 那么
F = F ∪{(xᵢ, AIᵢ(f), nᵢ,₀, nᵢ,₁)};
将 F中 AIᵢ(f)的最小值记为 AImin(f)；
E = E ∪{(xᵢ, AIᵢ(f), nᵢ,₀, nᵢ,₁) ∈ D|AIᵢ(f) = AImin(f), i ∈ I};
NAImin(f) = #E；
输出 E, NAImin(f).

4 基于理论结果的对基于LFSR的流密码的猜测然后代数攻击

设计者通常选择最大代数免疫布尔函数作为基于LFSR的密钥流生成器的滤波器，这有助于最大程度地抵抗传统代数攻击。第3节表明，对于具有最优代数免疫性的布尔函数 $ f $，有 $ \text{AI} {\min}(f) \leq \text{AI}(f) $。即使 $ \text{AI}(f) $ 不是最大值，仍有可能满足 $ \text{AI} {\min}(f) < \text{AI}(f) $。我们考虑利用 $ \text{AI}_{\min}(f) $ 的性质来恢复线性反馈移位寄存器的初始状态。

在猜测‐确定攻击中，猜测策略非常重要。在本节中，我们将给出一种猜测然后代数攻击，该攻击利用第3节中提出的 $ \text{AI} {\min}(f) $ 的性质，采用某种特定的猜测策略。首先，我们选择猜测线性反馈移位寄存器的一些（初始）内部状态比特，从而得到次数为 $ \text{AI} {\min}(f) $ 的方程。这里我们尽可能充分利用每一个已猜测的比特，即利用每个已猜测的比特构造尽可能多的低次方程。所猜测的线性反馈移位寄存器内部状态比特的位置应根据线性反馈移位寄存器的具体结构、滤波布尔函数的性质以及滤波抽头位置来遵循一定的规则。在猜测了适当数量的（初始）内部状态比特后，我们可以得到一个次数为 $ \text{AI}_{\min}(f) $ 的方程组。

接下来，我们将利用第3节中的理论结果提出一种攻击方法。我们关注的是基于线性反馈移位寄存器并采用非线性滤波的密钥流生成器如图1所示。与第2节中的描述相同，我们的目标是通过求解以下方程组来恢复初始状态比特 $ s_0 = (s_0, s_1, …, s_{l-1}) $：

$$
\begin{cases}
c_0 = f(s^1_0, s^2_0, …, s^n_0) \
c_1 = f(s^1_1, s^2_1, …, s^n_1) \
c_2 = f(s^1_2, s^2_2, …, s^n_2) \
\vdots
\end{cases}
\quad (2)
$$

其中，$ s^i_t,\ i=1,2,…,n $ 是在时刻 $ t $ 作为滤波布尔函数 $ f(x_1, x_2, …, x_n) $ 输入所选取的 $ n $ 个线性反馈移位寄存器状态比特。

猜测然后代数攻击：

假设线性反馈移位寄存器向右移位，并且是规则时钟驱动的。

步骤I ：对于 $ f(x_1, x_2, …, x_n) \in B_n $，通过算法1计算 $ \text{AI} {\min}(f) $、$ E $ 和 $ \text{NAI} {\min}(f) $。假设我们得到
$ E = {(x_{i_1}, \text{AI} {\min}(f), n {i_1,0}, n_{i_1,1}), …, (x_{i_m}, \text{AI} {\min}(f), n {i_m,0}, n_{i_m,1}) : 1 \leq i_1 < i_2 < \cdots < i_m \leq n} $，
$ \text{NAI} {\min}(f) = m $，$ \text{AI} {\min}(f) = k $。

步骤II ：根据步骤I得出的参数，我们执行以下操作:

(1) 在时刻 $ t $，将滤波函数的输入记为 $ s^1_t, …, s^n_t $，在集合 $ E $ 中找到对应于 $ x_{i_1} $ 的线性反馈移位寄存器状态比特，并将其记为 $ s^{i_1}_t $。

(2) 猜测 $ s^{i_1} t = a $，其中 $ a \in {0, 1} $，然后我们可以推导出一个方程
$$
f_t(s^1_t, s^2_t, …, s^{i_1-1}_t, a, s^{i_1+1}_t, …, s^n_t) = c_t.
$$
从算法1我们得到 $ \text{AI}(f_t) = \text{AI} {\min}(f) = k $。

(3) 对于每一次时钟，设对应于变量 $ x_i $ 和 $ x_j $ 的线性反馈移位寄存器状态比特位置之间的距离为 $ d_{i,j} $。注意到 $ E = {(x_{i_1}, \text{AI} {\min}(f), n {i_1,0}, n_{i_1,1}), …, (x_{i_m}, \text{AI} {\min}(f), n {i_m,0}, n_{i_m,1}) : 1 \leq i_1 < i_2 < \cdots < i_m \leq n} $，然后我们将流密码从时间 $ t $ 开始推进 $ d_{i_1,i_2} $ 个时钟。在时间 $ t + d_{i_1,i_2} $ 处于集合 $ E $ 中找到对应于 $ x_{i_2} $ 的线性反馈移位寄存器状态比特，并将其记为 $ s^{i_2} {t+d {i_1,i_2}} $。利用密钥流比特 $ c_{t+d_{i_1,i_2}} $ 和对 $ s^{i_1} t = a $ 的猜测值，通过将 $ s^{i_2} {t+d_{i_1,i_2}} $ 替换为 $ a $，我们在时间 $ t + d_{i_1,i_2} $ 得到另一个方程：
$$
f_{t+d_{i_1,i_2}}(s^1_{t+d_{i_1,i_2}}, …, s^{i_2-1} {t+d {i_1,i_2}}, a, s^{i_2+1} {t+d {i_1,i_2}}, …, s^n_{t+d_{i_1,i_2}}) = c_{t+d_{i_1,i_2}}.
$$

同样地，我们可以得到一组 $ m $ 个方程，并且函数 $ f_t, f_{t+d_{i_1,i_2}}, …, f_{t+d_{i_1,i_m}} $ 的代数免疫性是 $ \text{AI}_{\min}(f) = k $。

$$
\begin{cases}
f_t(s^1_t, …, s^{i_1-1} t, a, s^{i_1+1}_t, …, s^n_t) = c_t \
f {t+d_{i_1,i_2}}(s^1_{t+d_{i_1,i_2}}, …, s^{i_2-1} {t+d {i_1,i_2}}, a, s^{i_2+1} {t+d {i_1,i_2}}, …, s^n_{t+d_{i_1,i_2}}) = c_{t+d_{i_1,i_2}} \
\vdots \
f_{t+d_{i_1,i_m}}(s^1_{t+d_{i_1,i_m}}, …, s^{i_m-1} {t+d {i_1,i_m}}, a, s^{i_m+1} {t+d {i_1,i_m}}, …, s^n_{t+d_{i_1,i_m}}) = c_{t+d_{i_1,i_m}}
\end{cases}
\quad (3)
$$

到目前为止，我们通过猜测一个线性反馈移位寄存器状态比特得到了 $ m $ 个方程。对于每个方程，我们可以推导出 $ n_{i_j, c_{t + d_{i_j,i_k}}} $（或当 $ c_{t+d_{i_j,i_k}} = 0 $ 时为 $ n_{i_j, c_{t + d_{i_j,i_k}}} + 1 $）个次数为 $ \text{AI} {\min}(f) $ 的方程，其中 $ n {i_j, c_{t + d_{i_j,i_k}}} $ 是在定义3中定义的。

我们希望已猜测的比特均为线性反馈移位寄存器的初始状态比特，这样可使分析更加简便。如果已猜测的比特并非全部为初始状态比特，则需要进行更细致的分析。通常，我们选择参数 $ t = 0 $，因为它可以使在所有猜测的线性反馈移位寄存器状态比特中，被猜测的初始比特数量尽可能多，从而使分析更加容易。

这里我们分析已猜测的比特均为线性反馈移位寄存器的初始状态比特的情况。假设我们猜测了 $ r $ 个初始LFSR状态比特，那么可以通过线性反馈移位寄存器的线性反馈递归得到以初始LFSR状态比特为变量的 $ r \cdot \sum_{1 \leq j < k \leq m} n_{i_j,c_{t+d_{i_j,i_k}}} $ 个方程。然后我们采用与[3]中提到的方法相同的分析方法来分析其复杂度。

在猜测了 $ r $ 个线性反馈移位寄存器初始状态比特后，我们将利用代数免疫性为 $ \text{AI}(f) $ 的滤波布尔函数 $ f $ 求解 $ l $ 个初始线性反馈移位寄存器状态比特的问题，转化为求解一个具有代数免疫性 $ \text{AI}_{\min}(f) $ 的滤波布尔函数对应的 $ l - r $ 个未知初始比特的问题。

当条件
$$
r \cdot \sum_{1 \leq j < k \leq m} n_{i_j,c_{t+d_{i_j,i_k}}} \geq \binom{l - r}{\text{AI} {\min}(f)}
\quad (4)
$$
满足时，求解从步骤II导出的方程组的时间复杂度为
$$
T_1 = N^\omega,
$$
其中 $ N = \binom{l - r}{\text{AI} {\min}(f)} $，且 $ \omega $ 是高斯消元的参数，本文采用 $ \omega = 3 $。恢复线性反馈移位寄存器初始状态的复杂度为
$$
T = 2^r N^\omega.
$$
我们需要的数据是
$$
D = \max\left(rm, \binom{l - r}{\text{AI}_{\min}(f)}\right).
$$

关键条件是满足不等式(4)。事实上，当 $ \text{AI} {\min}(f) $ 足够小（特别是当 $ \text{AI} {\min}(f) = 1 $）时，该条件在大多数情况下可以满足。在这种情况下，我们可以直接看出，数据复杂度优于[3]中代数攻击的数据复杂度。然而时间复杂度的改进并不确定。可以推导出，当 $ r $ 满足以下不等式时，我们攻击的时间复杂度小于传统代数攻击在[3]中给出的时间复杂度：
$$
\frac{r}{\omega} < \log_2\left(\binom{l}{d}\right) - \log_2\left(\binom{l - r}{k}\right),
\quad (5)
$$
其中 $ r $ 是猜测的初始状态比特数，$ d = \text{AI}(f) $、$ k = \text{AI}_{\min}(f) $ 和 $ \omega $ 是高斯消元的参数。

事实上，如果充分利用 $ f| {x_i=c} $ 的零化子，则通过猜测 $ r $-比特初始状态所能得到的方程数量可能超过 $ r \cdot \sum {1 \leq j < k \leq m} n_{i_j,c_{t+d_{i_j,i_k}}} $。设 $ G = {g \in \text{AN}(f| {x_i=c}) \mid \deg(g) = \text{AI} {\min}(f)} $，对于元素 $ g \in G $，将其与次数小于 $ \text{AI}_{\min}(f) $ 的单项式相乘至 $ g $，我们可能会得到可用于构造方程的新多项式。

我们的方法为基于线性反馈移位寄存器的流密码所采用的滤波布尔函数提出了一种新的设计准则 $ f $，即密钥流生成器的参数不应同时满足不等式（4）和不等式（5），这意味着设计者应注意其密钥流生成器应满足以下条件：
(a) $ \text{AI} {\min}(f) $ 应足够大，以抵抗我们的猜测然后代数攻击。
(b) 对应于 $ \text{AI} {\min}(f) $ 的变量数量不应过大。

请注意，我们的方法适用于所有类型的具有非线性滤波的基于LFSR的流密码。如果目标流密码满足不等式（4）和（5），则我们可以降低时间和数据复杂度。

5 我们的方法在忽略我们准则的基于线性反馈移位寄存器的流密码上的应用

在本节中，我们给出一个例子，以说明非线性滤波布尔函数的 $ \text{AI}_{\min}(f) $ 不应过小。

目标模型与图1中所示的模型相同。LFSR的长度为80，其初始状态比特为 $ (s_0, s_1, …, s_{79}) $。线性反馈多项式是本原的。滤波布尔函数是一个9变量的布尔函数 $ f = f(x_1, x_2, …, x_9) $，$ \text{AI}(f) $ 是最优的。假设LFSR左移且为规则时钟驱动。$ f $ 的9个输入根据此完全正差集从LFSR中选取：(0,1,3,7,12,20,30,44,65)。

由上述描述可知，该模型能够在最大程度上抵御文献[3]中给出的传统代数攻击。接下来我们将说明，尽管 $ \text{AI}(f) $ 是最优的，但如果该模型违背了第4节中提到的我们的准则，则我们的方法仍然有效。

假设 $ \text{AI} {\min}(f) = 1 $，且对应的变量为 $ x_7 $，即 $ \text{AI}(f| {x_7=0}) = \text{AI}(f|_{x_7=1}) = 1 $，这意味着该模型违背了我们的准则。

根据第4节给出的猜测然后代数攻击，我们可以猜测 $ r = 41 $ 个初始状态比特 $ (s_{38}, s_{31}, …, s_{79}) $。然后我们可以得到至少41个线性方程，这些方程满足不等式（4），即 $ r \geq \binom{80 - r}{\text{AI} {\min}(f)} = 39 $。我们这种攻击的时间复杂度是
$$
T = 2^r \left( \binom{80 - r}{1} \right)^\omega = 2^{56.86},
$$
其中 $ m $ 是对应于 $ \text{AI} {\min}(f) $ 的 $ f $ 的变量数量。数据复杂度为
$$
D = \max\left(r, \binom{80 - r}{1}\right) = 2^{5.36}.
$$
内存复杂度为
$$
M = 2^{10.72}.
$$

表3显示了我们的方法（GA）与传统攻击（AA）在该模型上的比较，如[3]中所述。

攻击方法	时间复杂度 T	数据复杂度 D	内存复杂度 M
我们的方法	$ O(2^{56.86}) $	$ O(2^{5.36}) $	$ O(2^{10.72}) $
代数攻击	$ O(2^{73.56}) $	$ O(2^{24.52}) $	$ O(2^{49}) $

注释1 ：这个例子验证了，尽管目标模型的滤波布尔函数具有最优代数免疫性，但如果它不满足我们的准则，分析人员仍然可以使用我们的猜测然后代数攻击来恢复初始状态，且时间和数据复杂度低于[3]中给出的传统代数攻击。

6 结论

本文引入了一个新的参数，称为布尔函数 $ f $ 的一阶最小代数免疫度 $ \text{AI} {\min}(f) $，并研究了 $ \text{AI} {\min}(f) $ 的一些理论性质。基于我们的研究成果，我们提出了一种针对带有非线性滤波布尔函数 $ f $ 的基于线性反馈移位寄存器的流密码的猜测然后代数攻击方法，该方法通过预先猜测部分状态比特，然后对其应用代数攻击。

我们的方法充分利用每一个已猜测的比特，尽可能生成大量次数小于或等于 $ \text{AI}(f) $ 的方程。在某些条件下，该方法的时间和数据开销低于传统代数攻击在[3]中的开销。我们的方法为带有非线性滤波的基于LFSR的密钥流生成器提出了一个新的设计准则。我们将该方法应用于一个使用最大代数免疫布尔函数 $ f $ 作为其滤波器的80级密钥流生成器，而 $ \text{AI}_{\min}(f) $ 非常小，这违反了我们的准则。我们的方法在时间、内存和数据复杂度方面均低于传统代数攻击。