全通系统传输函数的延迟MATLAB仿真

理论分析

公式总结

一阶全通滤波器：

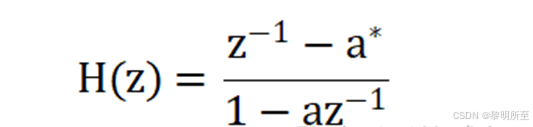
N阶级联：

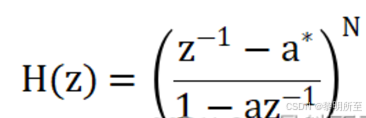
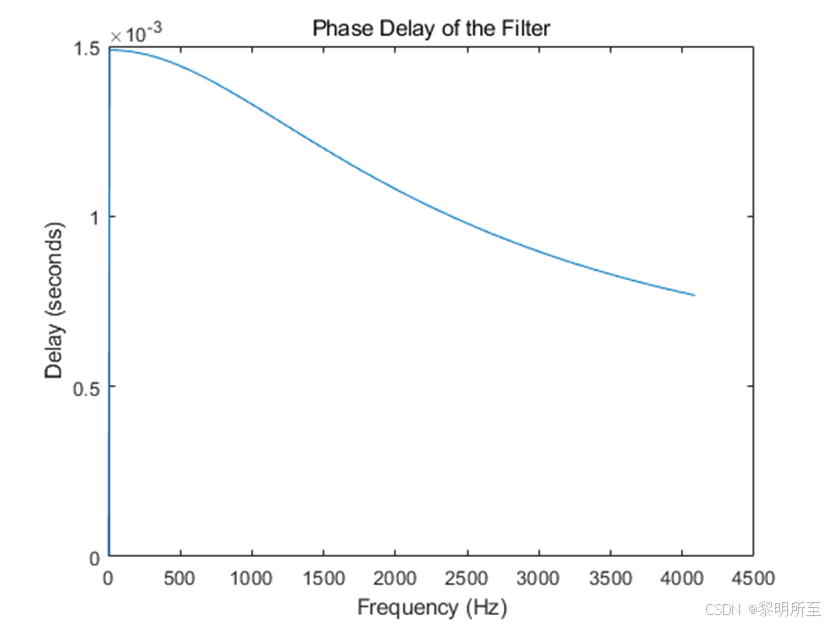
相位延迟：

群延迟：

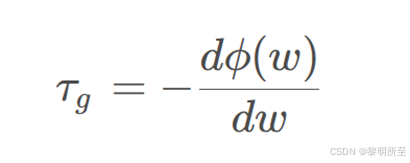
构造一阶IIR全通滤波器

format long

w=0:pi/255:pi;

num1=[-0.32,1];

den1=[1,-0.32];

h=freqz(num1,den1,w);

N=10; %构造一个一阶的IIR全通滤波器

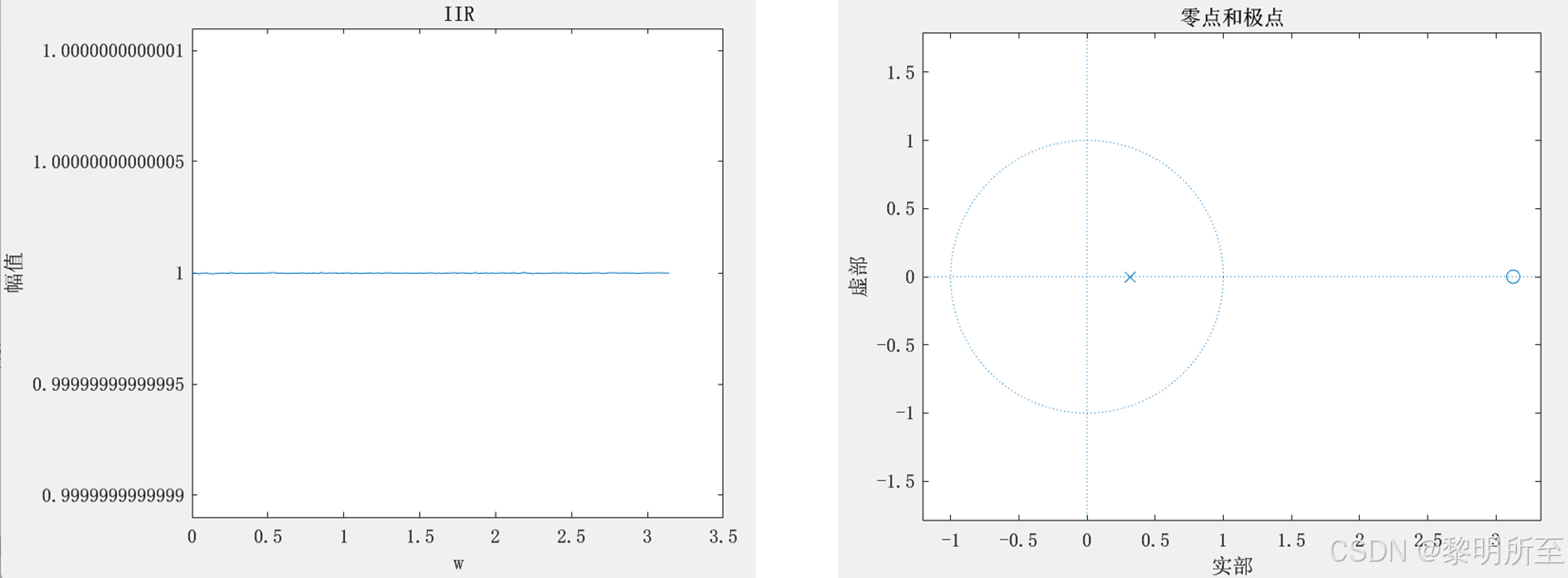
关于实稳定全通函数在频率范围从w=0到w=pi之间的相位变化，因果稳定实系数全通传输函数A(z)的群延迟函数     在区间0≤ω≤π上处处为正可以证明，一个M阶稳定实全通传输函数满足性质如下：

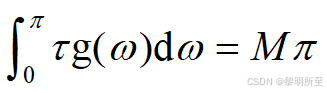
实验分析

相位延迟与群延迟

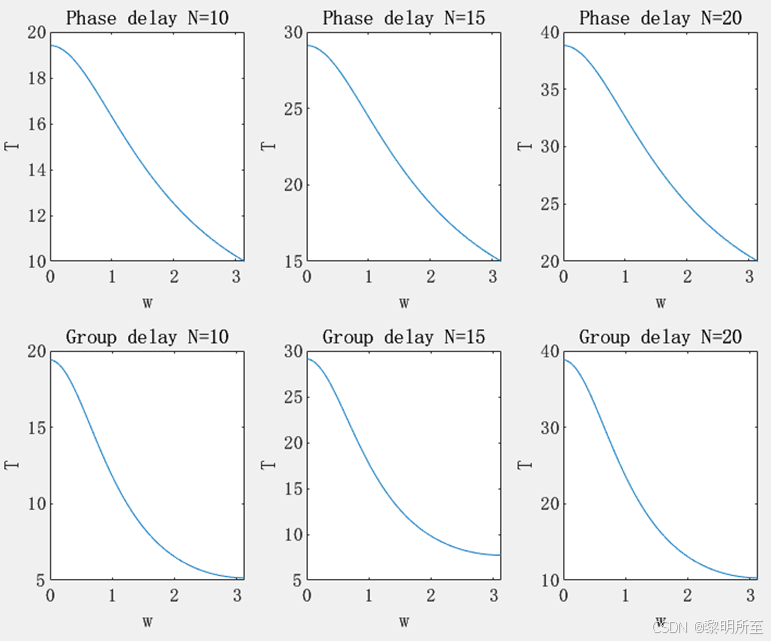
相位延迟：随着阶数 N 的增加，系统的总相位延迟在每个频率点上会增加。对于一阶全通滤波器，相位延迟通常是频率的函数，并且是非线性的。当级联 N 个一阶全通滤波器时，总的相位延迟将是单个一阶滤波器相位延迟的 N 倍，同群延迟。

群延迟：理想中，全通系统的群延迟（即相位延迟的导数）应该是恒定的，因为全通系统设计上旨在保持信号的包络通过时间不变。然而，如果系统的相位响应是非线性的，那么群延迟也将随频率变化，不再是常数。随着级联阶数 N 的增加，即使是小的相位非线性也可能会累积起来，导致在某些频率下相位延迟和群延迟的显著变化。

N=10、15、20时的相位时延和群时延:

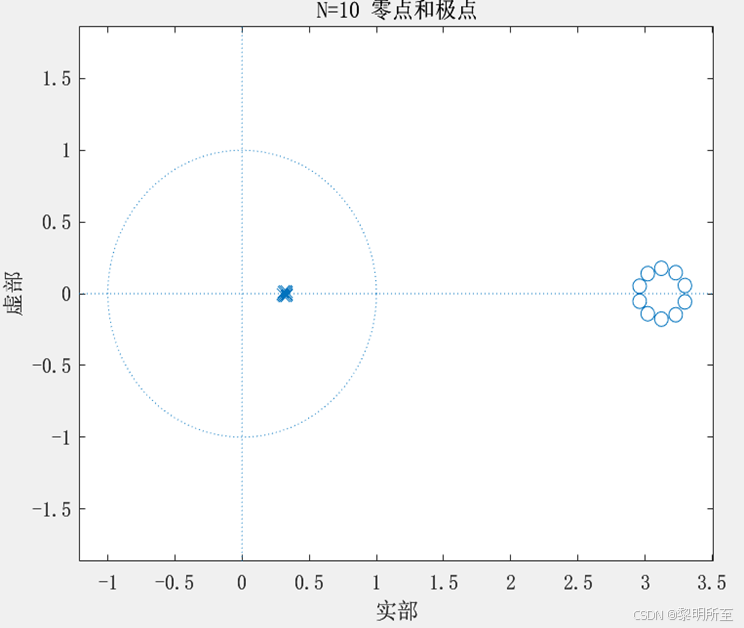
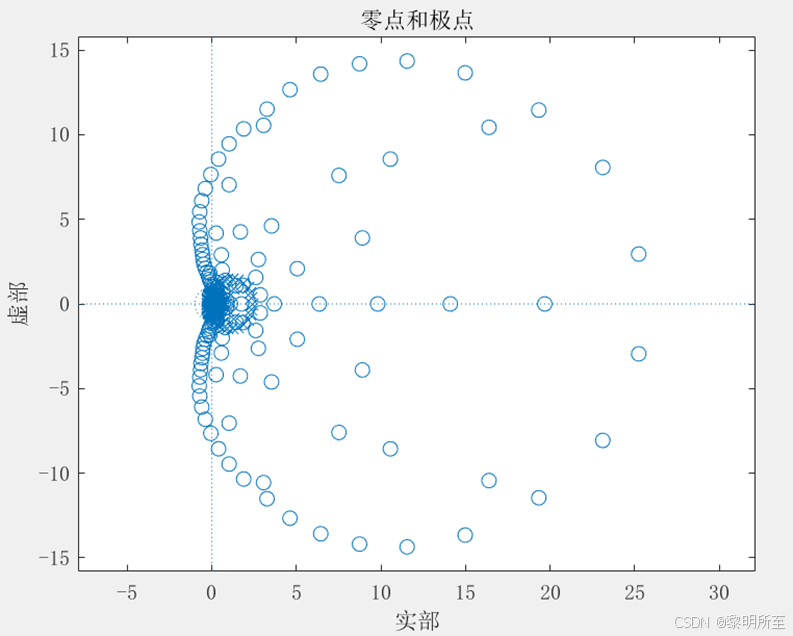
如右图，N=10时，得到的零点和极点发生变化不再是原来的3.125和0.32，N=140时，明显能看出来失真。

结果及误差分析

num=num1;

for i=1:N-1

num=conv(num,num1);

end

den=den1;

for i=1:N-1

den=conv(den,den1);

End

[z,p,k] = tf2zp(num,den);

figure

zplane(z,p);

音频滤波

设置滤波器：

num1=[-0.32,1];

den1=[1,-0.32];

N1=10;

num=num1;

for i=1:N1-1

num=conv(num,num1);

end

den=den1;

for i=1:N1-1

den=conv(den,den1);

end

yn1 = filter(num, den, y);

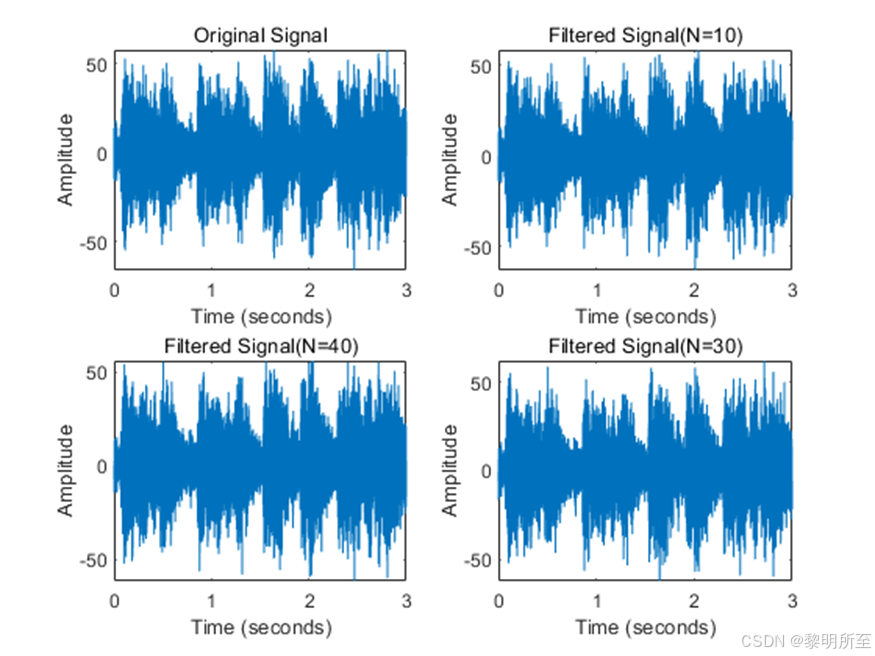
音频fs=8k

     随着阶数 N 的增加，系统的总相位延迟在每个频率点上会增加。对于一阶全通滤波器，相位延迟通常是频率的函数，并且是非线性的。当级联 N 个一阶全通滤波器时，总的相位延迟将是单个一阶滤波器相位延迟的 N 倍。

       音频经过N阶滤波器后，产生了相位延迟，阶数越高，延迟越久。原音频频率越大，延迟越低。

CODE：

clear
clc
format long
w=0:pi/255:pi;
num1=[-0.32,1];
den1=[1,-0.32];
h=freqz(num1,den1,w);
N=10;
num=num1;
for i=1:N-1
num=conv(num,num1);
end
den=den1;
for i=1:N-1
den=conv(den,den1);
end
H=h.^N;
%显示零点和极点
[z,p,k] = tf2zp(num,den);
figure 
zplane(z,p); 
title('零点和极点');
figure;%计算幅频响应
plot(w,abs(h)); 
title('IIR'); 
xlabel('w'); 
ylabel('幅值');
figure
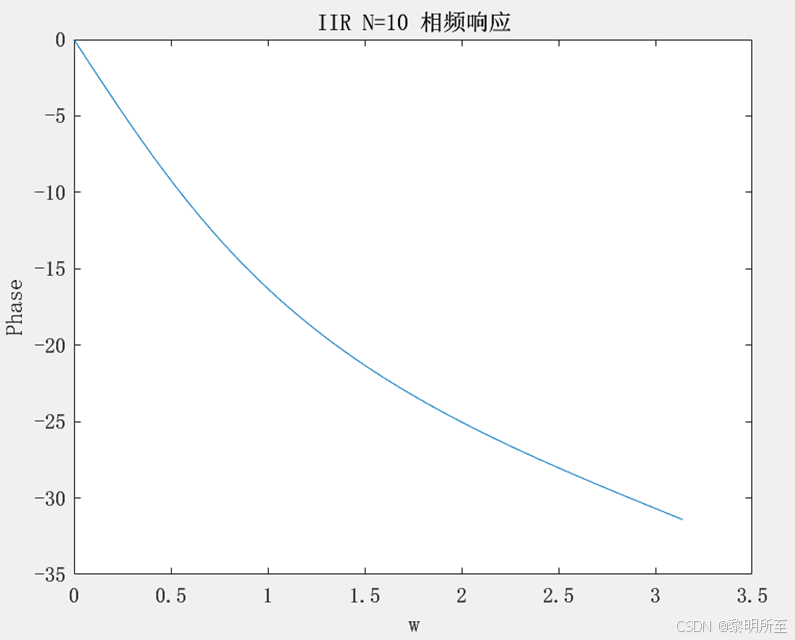
plot(w,unwrap(angle(H)));
title('IIR N=10 相频响应');
xlabel('w');
ylabel('Phase’);
figure;
subplot(2,3,1);%计算相位延迟
plot(w,-unwrap(angle(H))./w);
title('Phase delay N=10');
xlabel('w');
ylabel('T');
% g=grpdelay(num,den,w); 
% figure;%计算群延迟
% plot(w,g);% 同下
subplot(2,3,4);%计算群延迟 
g=-diff(unwrap(angle(H)))./diff(w); 
plot(w(1:255),g);
title('Group delay N=10'); 
xlabel('w’); 
ylabel('T');