一、单缸发动机曲轴连杆活塞系统动力学分析参考:
汽车动力总成系统/(伊朗)贝赫鲁兹.马沙迪,(英)戴维.克罗拉著;
白先旭,刘勇强译。——北京:机械工业出版社,2018.6
(汽车先进技术译丛.汽车创新与开发系列)
书名原文:Vehicle Powertrain Systems
ISBN 978-7-111-60005-3
曲柄连杆机构受力分析







燃烧室压力如下:
X_Column(turn_mn) Y_Column(deg) Z_Column(N_m2)
3000 0 1.82E+06
3000 20 3.24E+06
3000 23 3.29E+06
3000 26 3.24E+06
3000 50 2.03E+06
3000 60 1.52E+06
3000 70 1.01E+06
3000 80 8.10E+05
3000 100 6.08E+05
3000 110 5.07E+05
3000 150 3.04E+05
3000 190 1.22E+05
3000 200 6.08E+04
3000 220 0.00E+00
3000 540 0.00E+00
3000 600 1.01E+05
3000 630 2.03E+05
3000 660 4.05E+05
3000 690 9.12E+05
3000 710 1.52E+06
3000 720 1.82E+06
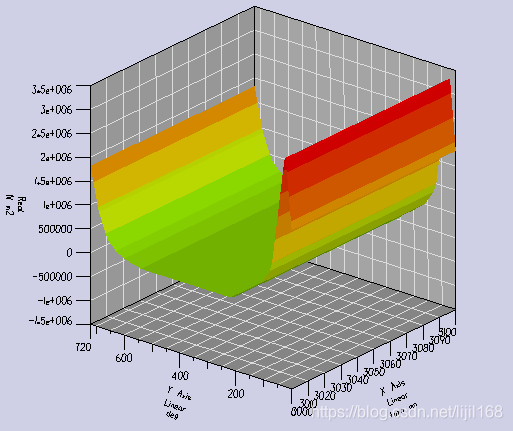
用matlab 编程求解结果如下:
1、活塞受力
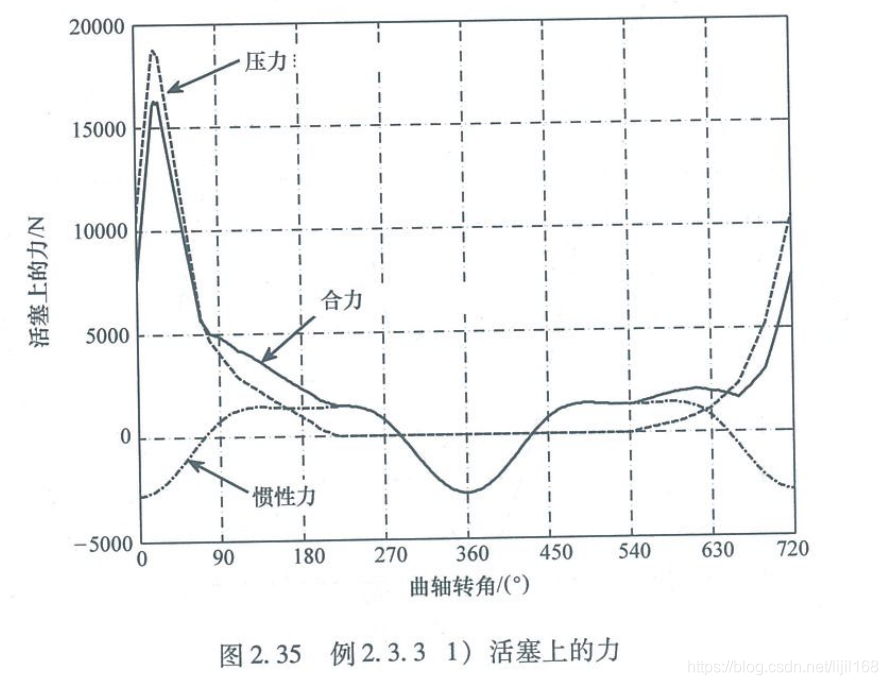
2、连杆惯性力
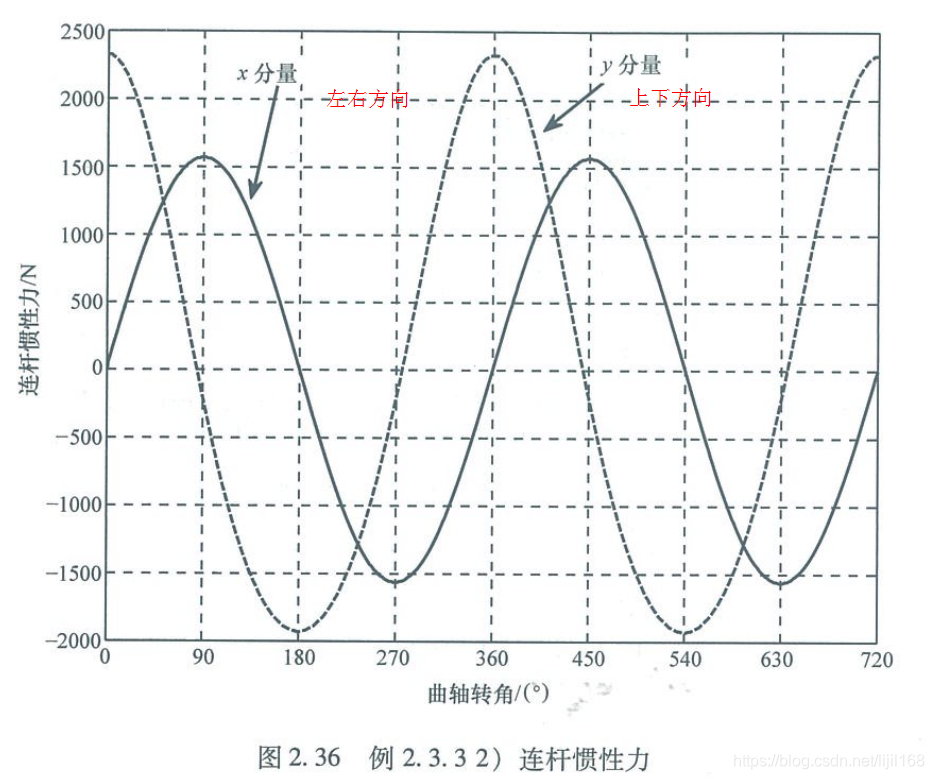
3、连杆惯性力矩
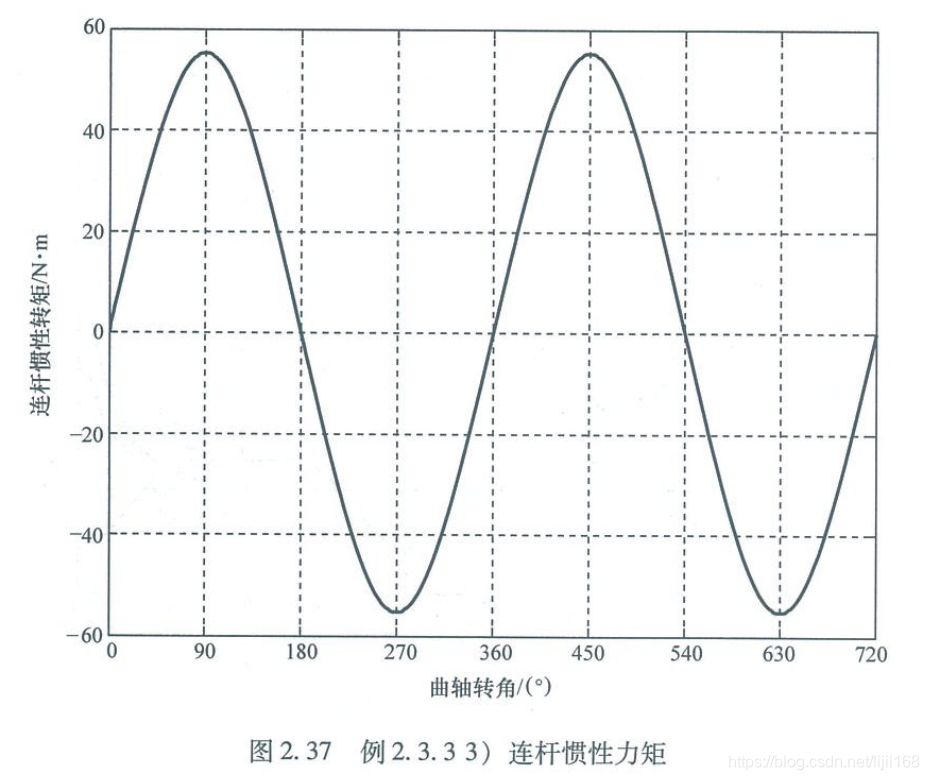
4、曲柄销轴承上的力
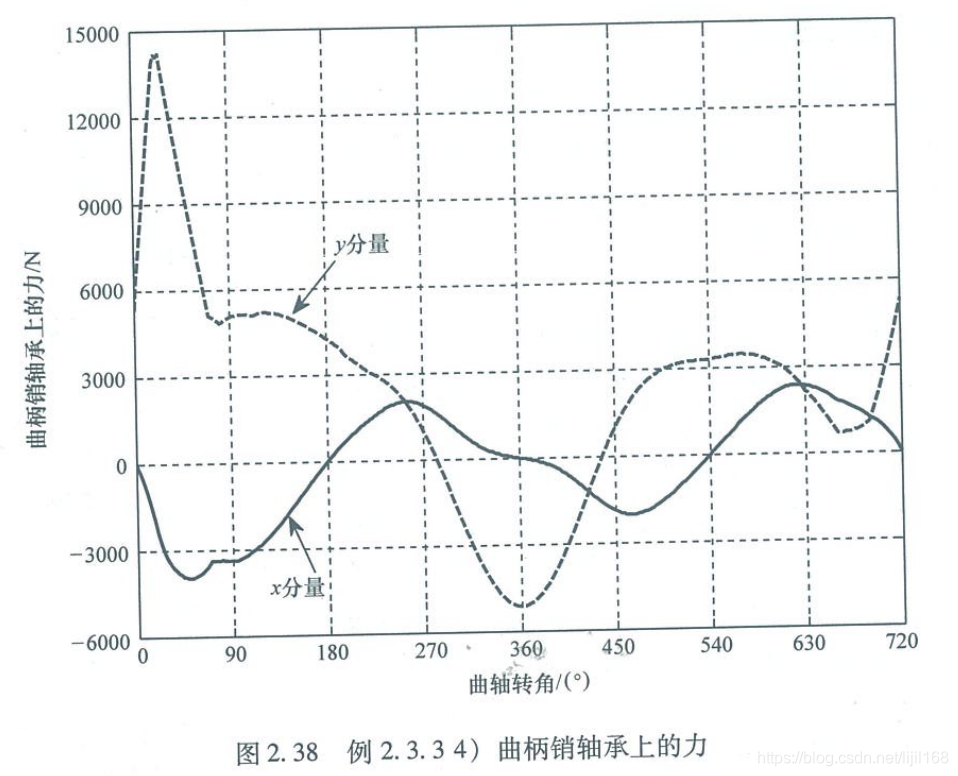
5、发动机转矩
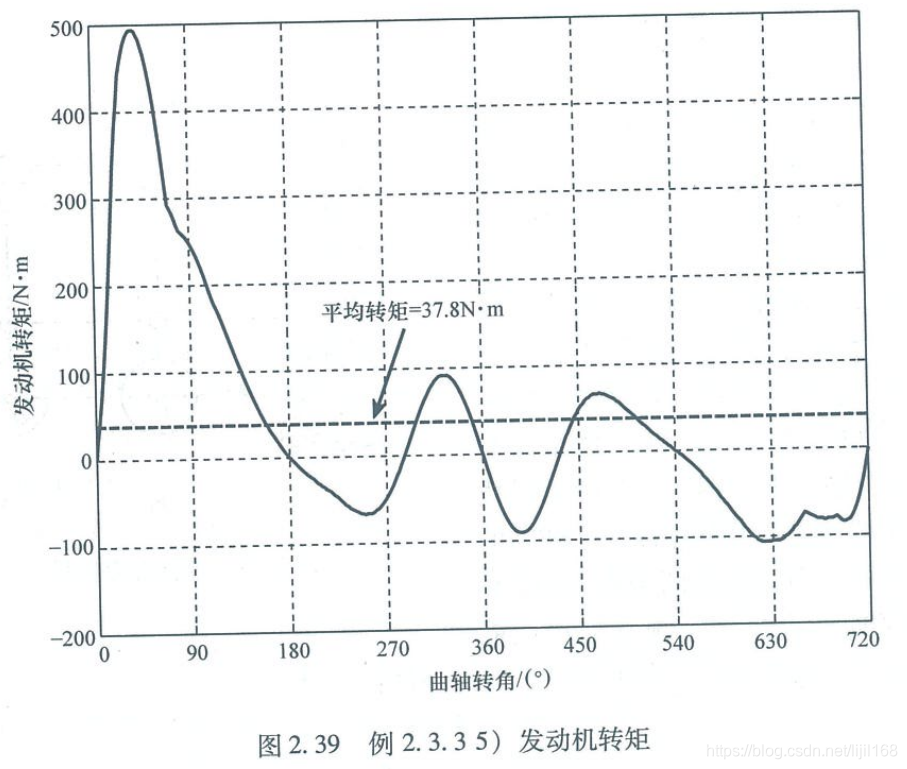
二、virtual.lab motion仿真
1、利用PDS建立单缸发动机模型,然后导入到virtual.lab motion中
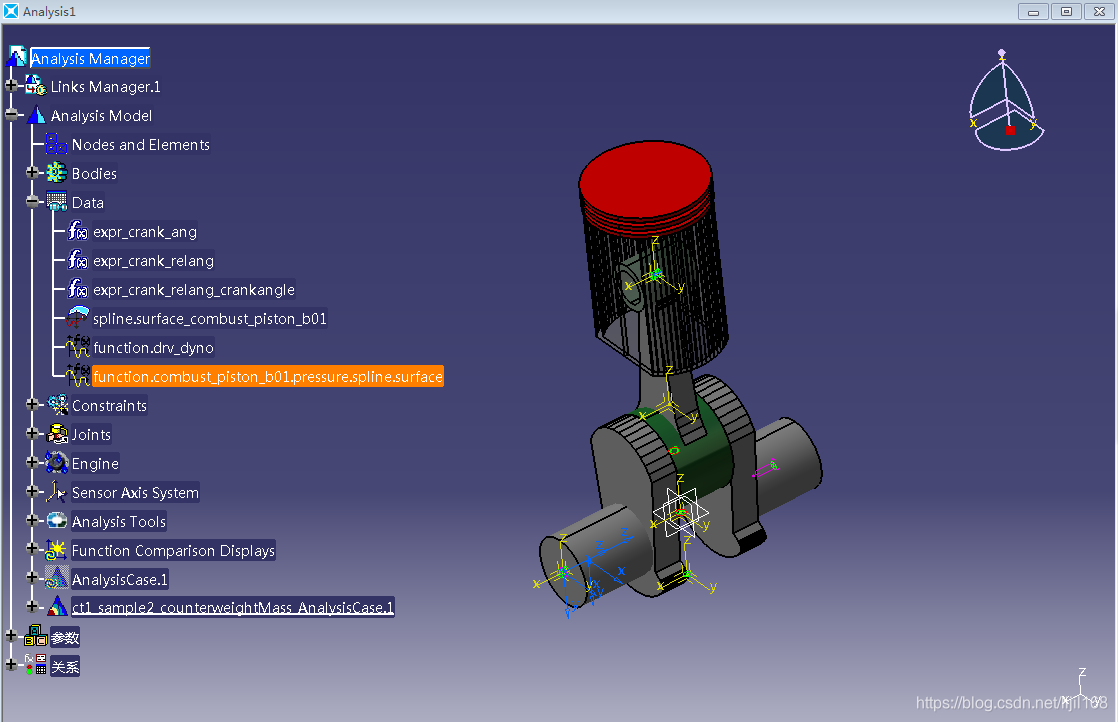
2、活塞轴向受力(活塞销受力)
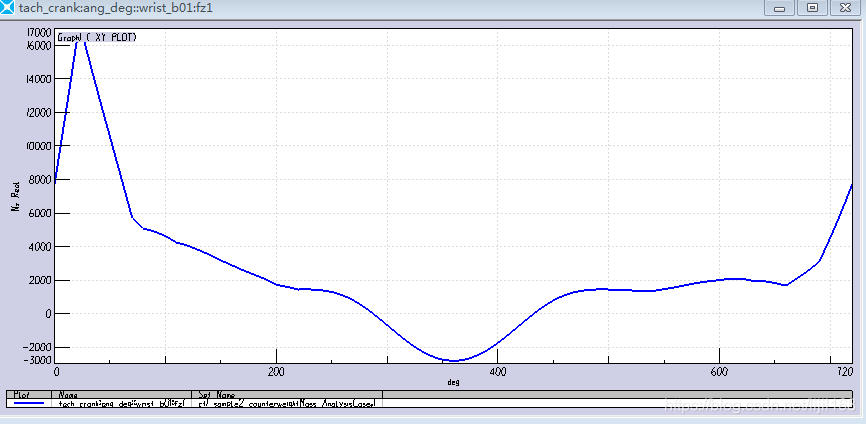
3、曲柄销轴承上的力
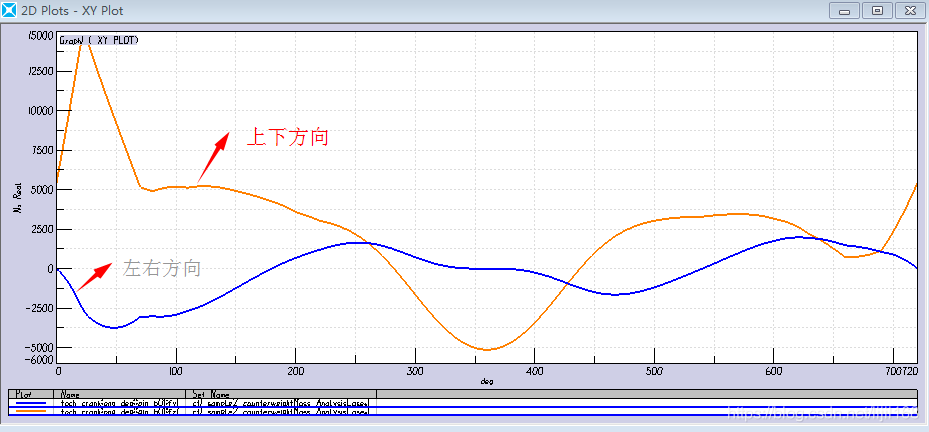
4、发动机转矩
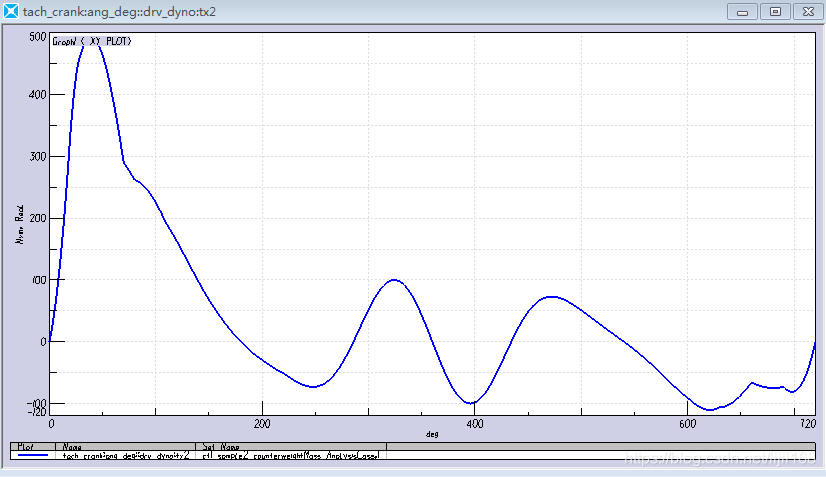
三、总结:virtual.lab motion 仿真的结果与理论计算的结果几乎完全一致!
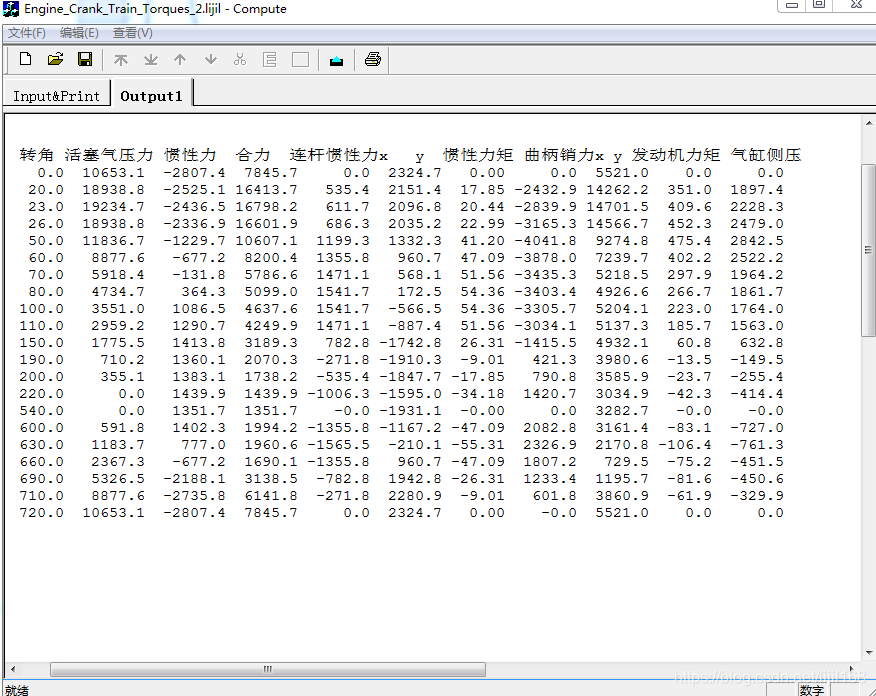
计算代码如下:
Example2.3.3-Single cylinder,4 stroke-engine torque
-----input-----
pi=3.141593;
mPiston=4.1; %kg
mConnectingRod=4.0; %kg
l=225/1000; %m,Connecting rod pin-pin length
lB=63.054/1000; %m,Connecting rod pin B-CG lengh
R=76/1000; %m,Crank radius
Ap=pi*61.5^2; %mm2,Pistion area
?IC=0.041687-mConnectingRod*lB^2; %kg.m2,Connecting rod inertia
-------Pressure in combustion chamber--------
pr[1][21]=[160.31,162.88,140.14,128.16,51.2,35.12,27.01,21.43,15.12,13.35,8.57,4.16,4.04,3.84,3.08,4.02,6.23,12.94,45.18,125.29,160.31]
ca[1][21]=[0,20,23,26,50,60,70,80,100,110,150,190,200,220,540,600,630,660,690,710,720]
i=0;
omega=1900;
omeg=omega*pi/30;
Rl=R/l; %define ratio R over l
lA=l-lB;
print("转角 活塞气压力 惯性力 合力 连杆惯性力x y 惯性力矩 曲柄销力x y 发动机力矩 气缸侧压")
while(i<21){
ang=ca[0][i]*pi/180
sa=sin(ang);
ca=cos(ang);
s2a=sin(2*ang);
c2a=cos(2*ang);
beta=asin(Rl*sa);
ka=ca+Rl*c2a/cos(beta)+Rl^3*s2a^2/cos(beta)^3/4;
//Piston acceleration:
aP=R*ka*omeg^2;
//Connecting rod angular acceleration:
alpha_c=Rl*omeg^2*sa/cos(beta);
//Connecting rod GC acceleration:
k3=lA*sa/l;
k4=ca+Rl*c2a*lB/cos(beta)/l;
agx=-R*omeg^2*k3;
agy=-R*omeg^2*k4;
ag=sqrt(agx^2+agy^2);
//Piston pressure force:
Fp=pr[0][i]*Ap/9.8;
//Piston inertia force:
FIP=-mPiston*aP;
//Resultant piston force:
FPt=Fp+FIP;
//Connection rod inertia forces(N):
FIx=-mConnectingRod*agx;
FIy=-mConnectingRod*agy;
//Conneting rod inertia torque(Nm):
TIG=IC*alpha_c;
//Crank-pin bearing forces:
Bx=(-FIP-Fp+lB*FIy/l)*tan(beta)-lA*FIx/l-TIG/l/cos(beta);
By=Fp+FIP-FIy;
//Engine torque:
Te=R*(By*sa-Bx*ca);
//气缸壁侧压力:
Fw=-FIx-Bx;
print("%5.1f %8.1f %8.1f %7.1f %7.1f %7.1f %6.2f %7.1f %7.1f %6.1f %7.1f",ca[0][i],Fp,FIP,FPt,FIx,FIy,TIG,Bx,By,Te,Fw)
i=i+1
}matlab 代码:
%Example2.3.3-Single cylinder,4 stroke-engine torque
%-----input-----
%pi=3.141593;
mPiston=430/1000; %kg
mConnectingRod=440/1000; %kg
l=140/1000; %m,Connecting rod pin-pin length
lB=37/1000; %m,Connecting rod pin B-CG lengh
R=49/1000; %m,Crank radius
Ap=5800; %mm2,Pistion area
IC=0.0015; %kg.m2,Connecting rod inertia
%-------Pressure in combustion chamber--------
pr=[18,32,32.5,32,20,15,10,8,6,5,3,1.2,0.6,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1.0,2.0,4,9,15,18];
crank_angle=[0,20,23,26,50,60,70,80,100,110,150,190,200,220,220,250,280,300,330,360,380,400,440,460,480,500,540,600,630,660,690,710,720];
pr=pr';
crank_angle=crank_angle';
%i=0;
omega=3000;
omeg=omega*pi/30;
Rl=R/l; %define ratio R over l
lA=l-lB;
%print("转角 活塞气压力 惯性力 合力 连杆惯性力x y 惯性力矩 曲柄销力x y 发动机力矩 气缸侧压")
%while(i<21){
ang=crank_angle*pi/180;
sa=sin(ang);
ca=cos(ang);
s2a=sin(2*ang);
c2a=cos(2*ang);
beta=asin((Rl*sa));
ka=ca+Rl*c2a./cos(beta)+Rl^3*s2a.^2./cos(beta).^3/4;
% //Piston acceleration:
aP=R*ka*omeg^2;
% //Connecting rod angular acceleration:
alpha_c=Rl*omeg^2*sa./cos(beta);
% //Connecting rod GC acceleration:
k3=lA*sa/l;
k4=ca+Rl*c2a*lB./cos(beta)/l;
agx=-R*omeg^2*k3;
agy=-R*omeg^2*k4;
ag=sqrt(agx.^2+agy.^2);
% //Piston pressure force:
Fp=pr*Ap/9.8;
% //Piston inertia force:
FIP=-mPiston*aP;
% //Resultant piston force:
FPt=Fp+FIP;
% //Connection rod inertia forces(N):
FIx=-mConnectingRod*agx;
FIy=-mConnectingRod*agy;
% //Conneting rod inertia torque(Nm):
TIG=IC*alpha_c;
% //Crank-pin bearing forces:
Bx=(-FIP-Fp+lB*FIy/l).*tan(beta)-lA*FIx/l-TIG/l./cos(beta);
By=Fp+FIP-FIy;
% //Engine torque:
Te=R*(By.*sa-Bx.*ca);
% //气缸壁侧压力:
Fw=-FIx-Bx;
%print("%5.1f %8.1f %8.1f %7.1f %7.1f %7.1f %6.2f %7.1f %7.1f %6.1f %7.1f",ca[0][i],Fp,FIP,FPt,FIx,FIy,TIG,Bx,By,Te,Fw)
%i=i+1
%}
subplot(2,3,1)
plot(crank_angle,[Fp,FIP,FPt]);%活塞气压力 惯性力 合力
title('活塞气压力 惯性力 合力')
subplot(2,3,2)
plot(crank_angle,[FIx,FIy]);%连杆惯性力x y
title('连杆惯性力x y')
subplot(2,3,3)
plot(crank_angle,TIG);%惯性力矩
title('惯性力矩')
subplot(2,3,4)
plot(crank_angle,[Bx,By]);%曲柄销力x y
title('曲柄销力x y')
subplot(2,3,5)
plot(crank_angle,Te);%发动机力矩
title('发动机力矩')
subplot(2,3,6)
plot(crank_angle,Fw);%气缸侧压
title('气缸侧压')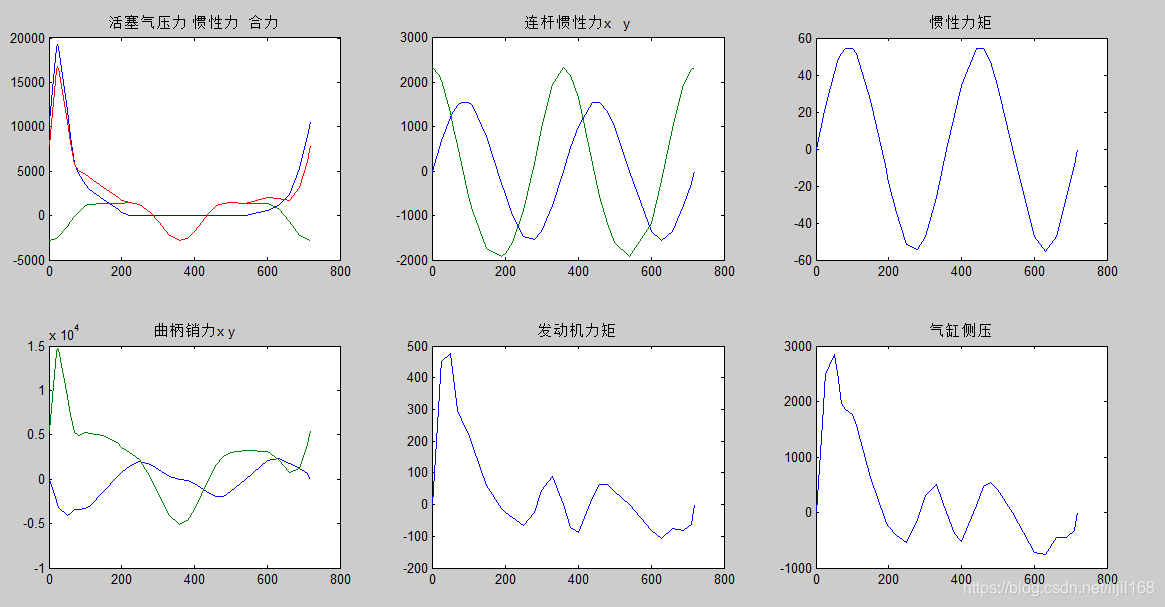











 本文详细解析了单缸发动机曲轴连杆活塞系统的动力学特性,包括活塞受力、连杆惯性力、曲柄销轴承力及发动机转矩等关键参数的计算方法。通过MATLAB编程实现理论计算,并与virtual.labmotion仿真结果对比,验证了计算的准确性。
本文详细解析了单缸发动机曲轴连杆活塞系统的动力学特性,包括活塞受力、连杆惯性力、曲柄销轴承力及发动机转矩等关键参数的计算方法。通过MATLAB编程实现理论计算,并与virtual.labmotion仿真结果对比,验证了计算的准确性。

















 782
782

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








