本文深入探讨了机器人学中DH参数的两种表示方法——标准DH和改进DH，详细解析了它们在坐标系设置、参数定义及坐标变换上的差异，并通过实例展示了如何应用这两种方法为机器人手臂建立坐标系。
浅尝辄止是乐趣，也导向惶恐
前言
这个学期开了“机器人学”的课程，学到了机器人手臂位置的表示，老师主要教的mDH，后来略微提到了sDH，在提到标准的DH表示后有不理解，于是自己钻研了一会，在在这里写下来，以防止以后自己再有不解，再者也是分享给诸位。
读本文的前提：掌握了基本的坐标变换，至少知道mDH或者sDH中一种
重要理解
1.一个连杆对应一个坐标系，坐标系代表了连杆的特征。
2.连杆与连杆之间的位置关系对应就是坐标与坐标的位置关系。
3.一个连杆的坐标系可以固连在连杆的任何位置，坐标系的轴方向也可以是任意，mDH与sDH只是规定了坐标系固连的位置与坐标系轴的朝向的一种建模方法。
4.DH表描述的是杆之间的关系
描述
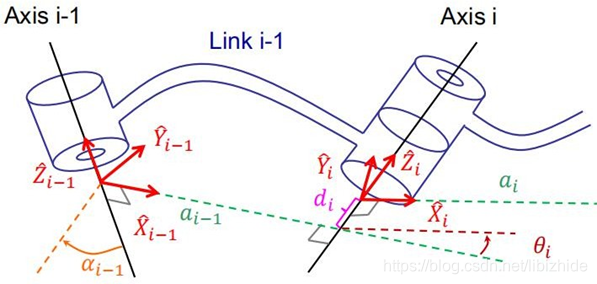
1.改进DH：连杆的坐标系放置在连杆的近端（即上一个关节i的位置），Z轴方向上一个i关节轴向平行（朝向可自拟定），X轴朝向上一个关节i轴向与下一个j关节j轴向的叉乘方向（即两关节的公垂线（公法线）方向）。
DH参数：（αi−1，ai−1，θi，di）（αi-1，ai-1，θi，di）（αi−1，ai−1，θi，di）
角度确定：
αi−1：以Xi−1方向看，Zi−1和Zi之间的夹角αi-1：以Xi-1方向看，Zi-1和Zi之间的夹角αi−1：以Xi−1方向看，Zi−1和Zi之间的夹角
ai−1：沿着Xi−1方向，Zi−1和Zi之间的距离ai-1：沿着Xi-1方向，Zi-1和Zi之间的距离ai−1：沿着Xi−1方向，Zi−1和Zi之间的距离
θi：以Zi方向看，Xi−1和Xi之间的夹角θi：以Zi方向看，Xi-1和Xi之间的夹角θi：以Zi方向看，Xi−
最低0.47元/天 解锁文章
扫一扫
2573
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
