最小转机问题；求解不带权图两点间最小距离；图的广度优先搜索

题目描述：

最少转机

时间限制: 1 s 空间限制: 512 MB
暑假来了， 你们一家打算坐飞机去旅游， 现在你们位于 S 号城市， 目标是 G 号城市，可是 S号城市并没不一定有直达 G 号城市的航班， 爸爸已经给你收集了很多航班的信息，现在希望聪明的你找到一种乘坐方式， 使得转机的次数最少（终点不计算在内）。 如果不可达， 请输出-1输入
第一行四个整数 n， k， s， g， 其中 n 表示城市总数， k 表示航线总数； s 表示起点城市编号， g 表示目标城市编号。接下来的 k 行， 每行是两个用空格分隔开的整数 a， b， 表示城市 a 和城市 b 之间有航线,
也就是城市 a 和城市 b 之间可以相互到达。
输出
1 个整数， 表示最少转机的次数。
样例输入
5 7 1 5
1 2
1 3
2 3
2 4
3 4
3 5
4 5
样例输出
1
说明

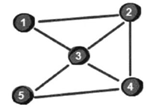
假设起点为 1 号城市， 终点为 5 号城市， 从 1 号城市到达 5 号城市， 中途在 3 号城市转了 1 次机。
数据规模
对于 100% 的数据，2≤n≤100， 1≤k≤200, 1≤s, g, a, b≤n

题目分析

本问题即求解不带权图两点间最小距离，可使用图的广度优先搜索，从开头节点开始，不断将其相邻节点压入队列，不断取出队首节点，计算其到达开头节点的距离（即边数），并标记此节点，再次压入相邻未被标记的节点入队列，直至队列为空。

C++代码

#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
#include <deque>
using namespace std;
struct graphNode
{
    int flag;
    int length;
    vector<int>access;
};
class graph
{
    vector<graphNode>myVector;
    int cityNumber=0,lineNumber=0;
    void addLine(int nodeID,int nodeID2);
public:
    void initGraph(int cityNumber,int lineNumber);
    void finishGraph();
    int getTurn(int cityNumber1,int cityNumber2);
};
void graph::initGraph(int cityNumber1,int lineNumber1)
{
    cityNumber=cityNumber1;
    lineNumber=lineNumber1;
    myVector.resize(cityNumber);
}
void graph::addLine(int nodeID,int nodeID2)
{
    myVector.at(nodeID).access.push_back(nodeID2);
    myVector.at(nodeID2).access.push_back(nodeID);
}
void graph::finishGraph()
{
    if(lineNumber==0)
        return;
    int k,j;
    for(int i=0;i<lineNumber;i++)
    {
        scanf("%d %d",&k,&j);
        addLine(k-1,j-1);
    }
}
int graph::getTurn(int cityNumber1,int cityNumber2)
{
    deque<int> myDeque;
    vector<int>::iterator i;
    int visitID;
    graphNode visit=myVector[cityNumber1-1];
    visitID=cityNumber1-1;
    int length=0;
    for(i=visit.access.begin();i!=visit.access.end();i++)
    {
        myDeque.push_back(*i);
        myVector.at(*i).flag=2;
        myVector.at(*i).length=1;
    }

    while(visitID!=cityNumber2-1&&myDeque.size())
    {
        visit=myVector.at(myDeque.at(0));
        visitID=myDeque.at(0);
        for(i=visit.access.begin();i!=visit.access.end();i++)
    {
        if(myVector.at(*i).flag!=2)
        {
            myDeque.push_back(*i);
            myVector.at(*i).flag=2;
            myVector.at(*i).length=myVector.at(myDeque.at(0)).length+1;
            length=myVector.at(*i).length;
        }
    }
        myDeque.pop_front();
    }
    cout<<myVector.at(cityNumber2-1).length-1;
}
int main()
{
    graph graph1;
    int i,j,k,h;
    cin>>i>>j>>k>>h;
    graph1.initGraph(i,j);
    graph1.finishGraph();
    graph1.getTurn(k,h);
}