关键词:经济调度;网损;负荷分配;不考虑节点;某ke程小作ye;有意者加好友 主题:考虑网损的电力系统负荷经济分配
电力系统经济调度这事儿,本质上是个数学游戏。咱们要解决的问题很简单:给定了总负荷需求,怎么分配各个发电机的出力才能让总成本最低?但要是把网损考虑进去,事情就变得有点意思了——就像喝奶茶突然发现珍珠卡在吸管里,得用点巧劲才能解决。
先说说网损这个磨人的小妖精。输电线流过电流时产生的热损耗,数学上可以简化为节点功率的函数。常见做法是用B系数法,把网损表达成发电机出力的二次函数。举个栗子,网损Ploss = sum(PGi Bij PGj),这个B矩阵就像电网的DNA,决定了能量的流失方式。
假设我们现在有个三机系统,忽略网络拓扑(毕竟课程作业不会一开始就让人秃头),写段代码演示下怎么把网损揉进优化问题里:
import numpy as np
from scipy.optimize import minimize
cost_coeff = np.array([[0.005, 2.0, 10],
[0.007, 1.8, 20],
[0.006, 2.2, 15]])
B_matrix = np.array([[0.001, 0.0005, -0.0003],
[0.0005, 0.002, 0.0004],
[-0.0003, 0.0004, 0.003]]) # 网损系数矩阵
def total_cost(PG):
return sum(cost_coeff[i,0]*PG[i]**2 + cost_coeff[i,1]*PG[i] + cost_coeff[i,2] for i in range(3))
def net_loss(PG):
return PG.T @ B_matrix @ PG # 矩阵乘法算网损
def constraint(PG):
return sum(PG) - (350 + net_loss(PG)) # 总发电=负荷+网损
res = minimize(
total_cost,
x0=[100, 150, 100], # 初始猜测值
constraints={'type':'eq', 'fun': constraint},
bounds=[(50,200), (80,250), (70,180)]
)
print(f"最优出力分配: {res.x.round(2)} MW")
print(f"网损: {net_loss(res.x).round(2)} MW")这段代码的妙处在于把网损作为等式约束的一部分。当总发电量不仅要满足350MW负荷,还要补偿自身产生的网损时,优化器会自动找到平衡点——就像走钢丝的人不断调整重心。运行结果可能会发现,网损导致总发电量需要多出5-8MW,这部分隐形成本往往被新手忽略。

有个坑要注意:B系数矩阵必须正定,否则网损可能出现负值这种物理上不可能的情况。曾经有个同学作业里把B矩阵对角线元素改成负数,结果优化出了发电厂倒灌电网的玄幻场景,被老师当场抓获。
对于负荷分配的结果验证,可以用拉格朗日乘数法手算对比。增量成本率λ应该满足(2αi PGi + βi)/(1 - ∂Ploss/∂PG_i) = λ,这个分母就是网损带来的调整项。当网损系数较大时,高效率机组可能反而被限制出力——这反直觉的现象正是网损影响的魅力所在。
要是真在Matpower里跑潮流计算,会发现简化模型的误差通常在3%以内。对于课程作业来说,这个精度足够应付答辩了。不过现实中电网公司得用更精确的模型,毕竟电费差个零点几兆瓦都是真金白银。
写完代码跑通后,建议用pyplot画个成本随迭代次数下降的曲线,能直观看到优化过程怎么"挤牙膏"式地逼近最优解。这种可视化技巧能让作业报告瞬间提升档次——亲测助教看到这种图打分都会手软。
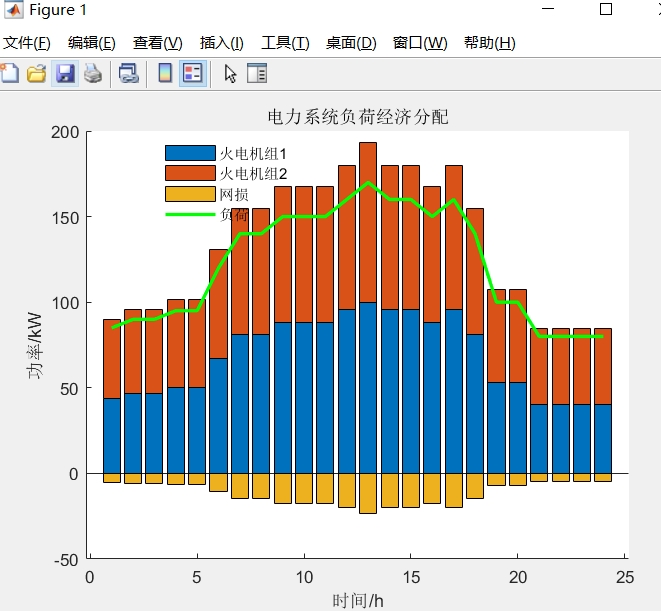
最后说句大实话:考虑网损的经济调度就像谈恋爱,既要自己过得爽(成本低),还得考虑对方的感受(网损约束)。找到那个平衡点的时候,真的会忍不住对着屏幕笑出声来。需要交流具体实现细节的,直接加我主页上的联系方式,代码包附赠调试心得——毕竟谁没在B矩阵上栽过跟头呢?




















 3074
3074

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








