1007 素数对猜想 (20分) （素数筛）

最新推荐文章于 2024-05-23 12:04:54 发布

原创最新推荐文章于 2024-05-23 12:04:54 发布 · 123 阅读

0 ·

CC 4.0 BY-SA版权

本文介绍了一种使用C语言实现的素数对计数方法，通过素数筛求解N以内的素数，并统计满足差为2的素数对。核心代码展示了如何运用数组操作来找出并计数这些特定的素数对。

PTA1007 素数对猜想 (20分)
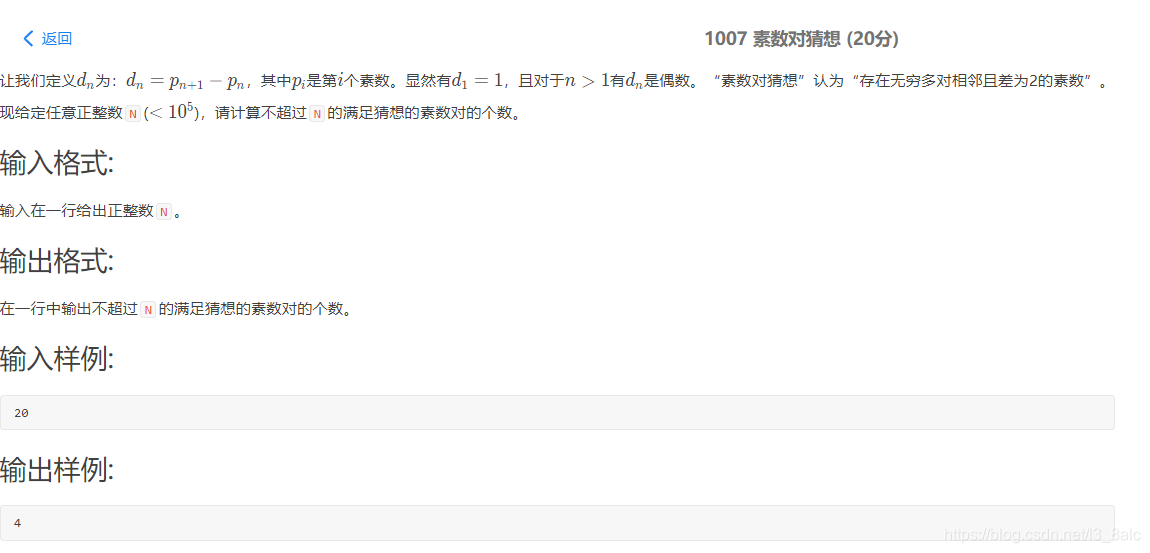
在这里插入图片描述

思路：用素数筛求的N以内的素数，把素数存在另一个数组内，满足条件t++

#include<stdio.h>
int n;
void isprime(int a[])//素数筛求n以内的素数
{	
	int i,j;
	for(i=2;i*i<=n;i++)
	 for(j=i+1;j<=n;j++)
	 	if(a[i]==0&&a[j]==0&&j%i==0)
	 	a[j]=1;
}
int main()
{	
	int i,k=0,a[100001]={0},b[100001]={0},t=0;
	scanf("%d",&n);
	isprime(a);
	for(i=2;i<=n;i++)
	if(a[i]==0)//把素数存放在另一个数组内
	{
		b[k]=i;
		k++;
	}
	for(i=1;i<k;i++)
	{
		if((b[i]-b[i-1])==2)//满足条件t++
		t++;
	}
	printf("%d",t);
	return 0;
		
	  
}