新型车辆避撞换道算法的性能评估
萨贾德·萨米、沙赫拉姆·阿扎迪、礼萨·卡泽米、阿诺·艾希伯格、 布朗科·罗吉奇和迈克尔·塞默
摘要
本研究提出了一种评估新型紧急换道算法性能的方法论。该算法基于车辆动力学和环境条件定义了一系列约束条件,以确保实现安全舒适的换道操作。所提算法的主要优势在于考虑了道路上其他车辆的横向位置、轮胎‐路面摩擦以及实时能力。为了评估所开发算法的性能,设计了一组驾驶场景,用以涵盖紧急变道操作中可能出现的不同交通状况。这些场景随后在IPG CarMaker这一车辆动力学平台上实现。基于所设计的场景,对算法在无碰撞换道操作中的效率进行了检验。
关键词 自动驾驶 Lane变道操作 Decision进行 碰撞避免
1 引言
汽车对我们的生活产生了巨大影响。它们是自由的象征,也常被用作自我表达的方式。但它们也可能给我们的生活带来负面影响。2010年,欧洲因交通事故导致28,759人死亡[1],美国则有32,999人因此丧生[2]。车道变换操作是导致交通事故的重要原因之一,尤其由于驾驶员在准确估计车辆间距[3]方面存在驾驶员错误所致。据统计,百分之二十的高速公路交通事故[4]是由不当的车道变换引起的。此外,车道变换是一种常见的驾驶操作,被认为是驾驶自动化进程中的下一步。同时,它也是微观交通仿真[5]的重要组成部分,对这些模型的分析结果具有显著影响。鉴于上述种种原因,自主变道[5]如今已成为汽车工程[5]领域的重要研究课题。
迄今为止,已有多种方法被用于车道变换的决策与路径规划。在[6]中,基于元胞自动机(CA)建立了一种车辆车道变换模型,该模型主要关注车辆的一些约束条件,如最大加速度和减速度。[6]中所使用的规则后来被另一项研究用于双车道和三车道宽幅高速公路的交通仿真[7]。研究表明,所开发的模型能够实现逼真的仿真效果。本研究采用一种软计算方法对车道变换过程中的驾驶员行为进行建模。为了构建一个涵盖复杂场景的更全面模型,所提出的系统不仅限于单输入单输出(SISO)[8]。
在另一项研究中,提出了一种能够识别路径边界、存储所获取信息并使用向量方法设计期望行驶路径的算法[9]。在[10]中,将驾驶任务解释为一种模型预测控制,该控制能够根据ISO标准利用模糊逻辑对双车道变换操作进行控制和稳定。上述方法还在另一项研究中被用于控制车辆速度以及车道变换操作[11]。在单向双车道道路上进行的实验表明,车辆的纵向和横向控制动作良好,与道路的交通状况相适应。
除了关于决策的研究外,许多研究还集中在路径规划技术上。一些模型是基于车辆动力学和驾驶员在变道操作期间的驾驶员策略而开发的。在实际驾驶条件下的实验评估表明,所提出的模型优于使用多项式进行路径规划的模型,并能生成更精确的路径[12, 13]。智能控制技术,如模糊控制[14]、神经网络[15]和群体智能[16],也被应用于路径规划。例如,在[17]中使用了神经网络来预测其他车辆的短期和长期运动。长期预测用于提醒驾驶员进行车道变换或避免车道变换,以防止可能发生碰撞。此外,短期预测帮助驾驶员应对交通流中的意外变化。
2 算法
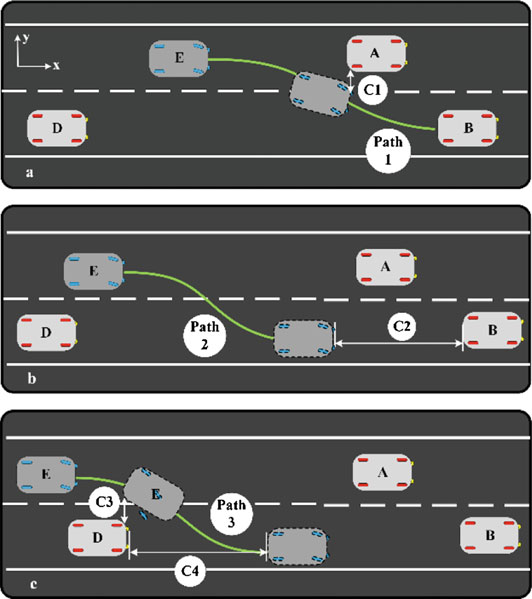
为了开发车道变换决策算法,首先,建立车辆横向运动关于操作时间的方程。然后,根据约束条件计算关键操作时间。最后,通过比较关键时间来决定执行该操作的可行性。假设在最坏情况下,变道操作过程中周围存在其他三辆车辆,如图1所示。车辆E表示自车(变道车辆),车辆A表示同一车道的前导车辆,车辆B和D分别表示目标车道的前导车辆和后方车辆。此外,图1中虚线车辆表示变道操作过程中的车辆E。如果满足以下四个条件,则变道操作是可行的;
- 在操作过程中,车辆E的右前角与车辆B的右后角之间的横向距离必须至少为 C1(图1a)。
- 车辆E完成操作并移动到目标车道后,其与车辆B之间的距离必须 ≥ C2(图1b)。
- 在操作过程中,车辆E的右后角与车辆D的左前角之间的横向距离至少应为 C3。此外,操作完成后,这两辆车之间的纵向距离至少应为 C4(图1c)。
- 车辆E在操作过程中产生的横向加速度必须是可实现的,需考虑道路与轮胎之间的有效摩擦潜力。
所提出的决策算法研究了在考虑上述所有约束条件的情况下设计轨迹的可能性。该算法以时间为主要决策参数。首先,推导出每项约束条件下最临界轨迹的车道变换持续时间;然后,通过比较计算的变道持续时间来决定是否进行车道变换。接下来,将描述基于前述各项约束条件计算临界轨迹的方法论。
2.1 情况1:同一车道上的前方车辆
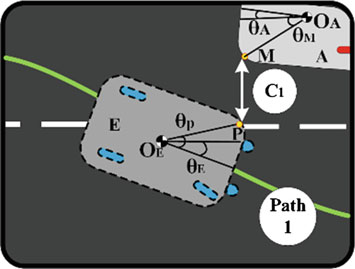
如图1a所示,在车道变换过程中,若C1为零,则车辆E的左前角(点P)将触碰到车辆A的右后角(点M)。这种情况的放大示意图如图2所示。
当车辆的纵向坐标重合时,考虑C1之间的安全距离,可得到公式(1)。
$$
y_A(t) - y_E(t) = C1 + |OAM| \cdot |\sin(\theta_M - \theta_A(t))| + |OEP| \cdot |\sin(\theta_P - \theta_E(t))|
\quad (1)
$$
在公式(1)中,$y_A(t)$ 和 $y_E(t)$ 分别表示车辆A和E的重心横向位置。$|OEP|$ 是连接车辆E’的重心与点P的假想线长度。类似地,参数 $|OAM|$ 表示车辆A’的重心与点M之间的假想线长度。$\theta_M$ 是OAM与车辆A的纵向轴之间的角度。参数 $\theta_A(t)$ 是车辆A的纵向轴与地平线之间的角度,而$\theta_P$是OEP与车辆E的纵向轴之间的角度。同时 $\theta_E(t)$ 表示在任意时刻车辆E的纵向轴与地平线之间的角度。利用[18]中提出的数值方法,可以求解(1),得到满足约束C1的机动持续时间。该时间标记为$t_1$。
2.2 情况2:目标车道前方车辆
多项研究探讨了两车之间最小安全纵向距离的问题,并为此距离提出了多种公式,例如[19, 20]。在本研究中,采用了Juala等人提出的方法[21]。在这种保守方法中,假设前车在与障碍物发生碰撞时速度突然降为零。在此情况下,安全距离计算如下:
$$
C2 = s_0 + v_{xE} t_d + \frac{v_{xE}^2}{2 a_{Eb}} \quad (2)
$$
在(2)中,$s_0$为安全停车距离,而$a_{Eb}$为车辆E的最大减速度。此外,$t_d$为驾驶员的反应时间,其取决于驾驶员的身心状况以及道路条件等多种因素,通常在0.67到1之间变化[22]。通过将所有所需参数代入(2),可得到C2,进而得到操作时间,记为$t_2$。因此,在指定时刻,两辆车的纵向和横向位置由(3)和(4)决定;
$$
x_B(t) - x_E(t) = s_0 + v_{xE} t_d + \frac{v_{xE}^2}{2 a_{Eb}} + l_{Ef} + l_{Br} \quad (3)
$$
$$
y_B(t) = y_E(t) \quad (4)
$$
其中,$x_B(t)$ 和 $y_B(t)$ 分别表示车辆B重心的纵向和横向位置,$l_{Br}$表示车辆B的重心到其后部的纵向距离。显然,该约束将操作结束时车辆E与车辆B的重心之间的纵向距离大于式(3)计算值的所有轨迹指定为安全轨迹的候选。
2.3 情况3:目标车道上有后方车辆
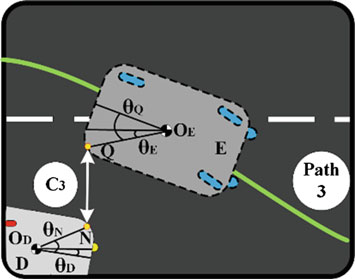
该案例是前两个案例的组合。本案例中车辆状态的更详细示意图如图3所示。
为了获得车道变换持续时间,首先基于安全横向距离使用(5)计算适当的操作时间。然后,使用操作结束时的安全纵向距离,通过(6)获得合适的操作时间。由于车辆D的行为由自动系统控制,发生突然速度变化的可能性几乎可以忽略不计,因此在情况二中采用两秒法则[23]代替保守方法。最后,将两个所得值中的较大值作为$t_3$。
$$
y_E(t) - y_D(t) = C3 + |ODN| \cdot |\sin(\theta_N - \theta_D(t))| + |OEQ| \cdot |\sin(\theta_E(t))| \quad (5)
$$
$$
x_E(t) - x_D(t) = 2 v_{xD} + l_{Er} + l_{Df} \quad (6)
$$
在公式(5)和(6)中,$x_D(t)$ 和 $y_D(t)$ 表示车辆D重心的纵向和横向位置。此外,$v_{xD}$ 和 $l_{Df}$ 分别表示车辆D的纵向速度以及车辆D重心到其后部的纵向距离。$|OEQ|$ 是车辆E重心与该车辆右后角(即点Q)之间假想线的长度。类似地,(5)中的 $|ODN|$ 表示车辆D重心到其左前角(点N)的假想线长度。$l_{Er}$是车辆E重心与其后部之间的纵向距离,而$\theta_N$ 表示该线与车辆纵向轴之间的角度。
2.4 情况4:最激进的车道变换
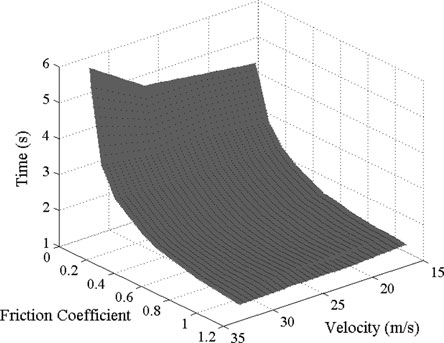
车辆的车道变换轨迹设计必须符合车辆动力学的可行性要求。换句话说,除了轨迹的连续性和可微性外,还必须满足车辆的动力学约束条件。特别是必须确保在操作过程中产生的横向加速度在考虑路面‐轮胎摩擦的情况下是可实现的,并能保持车辆稳定性。分析中使用了动态车辆仿真工具IPG CarMaker。图4展示了质量、速度和轮胎‐路面摩擦条件下操作时间的三维图。所示曲面将空间分为两部分,曲面上方的体积表示可接受的操作时间。
不同仿真的结果由(7)近似表示,其中最小操作时间$t_m$用路面‐轮胎摩擦$\mu$和车辆速度$v_x$表示。
$$
t_m(l, v_x) = \frac{l}{8 + 0.5 v_x} + 5 / 10l \quad (7)
$$
2.5 决策策略
本文中,基于上述方程获取$t_1$,$t_2$和$t_3$所需的参数值列于表1中。
通过计算和比较这些时间,可以做出决策。表2列出了可能的变道情况以及该操作可接受的时间或时间间隔。显然,如果计算出的时间与表2中列出的任何案例均不相符,则不允许执行变道操作。如果路径上不存在三辆车A、B和D中的任意一辆,则将其对应的时间从计算中排除。
| 参数 | 值 | 参数 | 值 |
|---|---|---|---|
| C1 | 1 (米) | wA | 1.65 (米) |
| lEr | 1.9(米) | lDf | 1.7(米) |
| wE | 1.56(米) | S0 | 2(米) |
| td | 0.5(秒) | aEb | 0.7 g(m/s²) |
| lEf | 1.6(米) | lBr | 1.8(米) |
表1 参数的取值
| No. | Case | Time | No. | Case | Time |
|---|---|---|---|---|---|
| 1 | t1 > t2 > t4 > t3 | [t2 t4] | 8 | t2 > t1 = t3 > t4 | t1 |
| 2 | t1 > t2 > t3 > t4 | [t2 t3] | 9 | t1 > t2 = t4 > t3 | t2 |
| 3 | t2 > t1 > t4 > t3 | [t1 t4] | 10 | t1 > t2 = t3 > t4 | t2 |
| 4 | t2 > t1 > t3 > t4 | [t1 t3] | 11 | t2 > t1 > t4 = t3 | [t1 t3] |
| 5 | t1 = t2 > t4 > t3 | [t1 t4] | 12 | t1 > t2 > t4 = t3 | [t2 t3] |
| 6 | t1 = t2 > t3 > t4 | [t1 t3] | 13 | t1 = t2 = t3 > t4 | [t1 t3] |
| 7 | t2 > t1 = t4 > t3 | t1 | 14 | t1 = t2 = t3 = t4 | t1 |
表2 决策表
3 场景设计
设计了包含所有不同可能交通状况的综合场景,以评估所开发的决策算法的性能。如前所述,该算法旨在使目标车辆在驾驶员无法控制车辆时,向道路的右侧车道进行车道变换。因此,变道方向始终为右侧。
在设计场景中,目标车辆行驶在一条三车道高速公路上,在最坏情况下,其周围有三辆其他车辆。这些场景基于道路上的车辆数量、所有车辆的相对距离、速度和加速度以及道路摩擦进行设计。为了更清晰地展示不同可能的交通情况,场景被参数化定义,如表3所示。
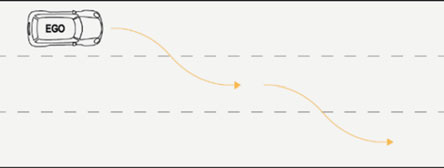
3.1 场景1:道路上无其他车辆
当道路上没有其他车辆时,会出现最简单的情况。决策单元根据自车的速度和道路条件定义合适的车道变换时间。这种情况如图5所示。
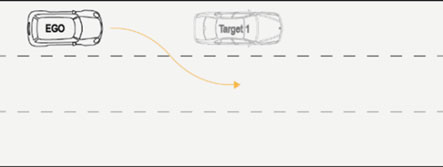
3.2 场景2:同一车道前方有车辆
当同一车道前方仅有一辆车辆时,会发生这种情况。根据车辆A(目标1)的动态行为,决策算法必须能够引导自车进行安全变道(图6)。
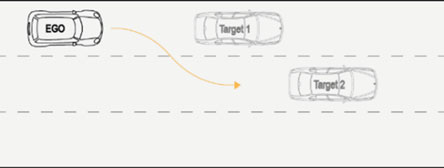
3.3 场景3:同一车道有一辆车,目标车道有一辆车
在此案例中,决策系统应考虑另外两辆车辆的情况和行为,以准备安全变道操作。此处,除了与自车在同一车道上行驶的车辆A之外,车辆B(目标2)正在目标车道上行驶。该情况如图7所示。
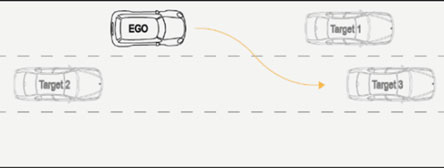
3.4 场景4:同一车道上有一辆车,目标车道上有两辆车
这是紧急倾斜变道操作中最复杂的情况,决策单元需要在道路上考虑其他三辆车辆的情况下引导自车。该情况如图8所示。
| 车辆 | 相对距离 (m) | 相对距离 (m) | 速度 (m/s) | 速度 (m/s) | 速度 (m/s) | 加速度 (m/s²) | 加速度 (m/s²) | 摩擦 |
|---|---|---|---|---|---|---|---|---|
| 变量 | 范围 | 变量 | 变量 | 范围 | 变量 | 范围 | 范围 | |
| Ego | – | [0 60] | vE | vE | [0 36] | aE | [−6 4] | [0.1 1.2] |
| 目标1 | s1 | [0 60] | v1 = vA | [0 36] | a1 = aA | [−6 4] | [0.1 1.2] | |
| 目标2 | s2 | [0 60] | v2 = vB | [0 36] | a2 = aB | [−6 4] | [0.1 1.2] | |
| 目标3 | s3 | [0 60] | v3 = vD | [0 36] | a3 = ac | [−6 4] | [0.1 1.2] |
表3 不同可能交通状况的参数化表示
4 在IPG CarMaker中实现场景
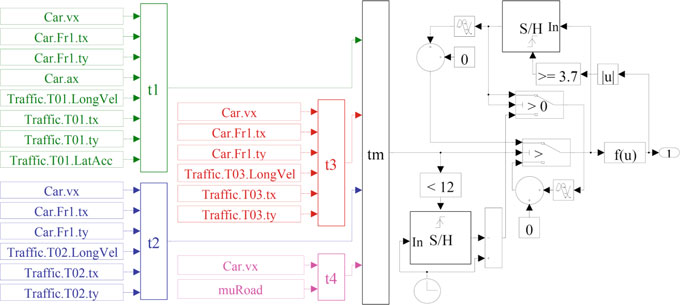
上述所有案例均在IPG CarMaker中实现,该平台用于模拟车辆动力学及控制单元。为此,利用该软件与MATLAB/Simulink的通信能力以获得更高灵活性。如前所述,在决策单元中实现了不同的约束条件,以确定每种案例中的合适时间 $t_1$ 至 $t_4$。根据计算出的时间,基于决策规则(表2)得出了执行安全变道的可能性以及相应的操作时间。图9显示了Simulink中最终系统的框图。
在图9中,自车和目标车辆的动态数据以及轮胎‐路面摩擦被输入到函数中,关键变道时间 $t_1$, $t_2$, $t_3$, 和 $t_4$ 根据第2节中给出的公式进行计算。这些时间随后被发送到决策功能模块,其中表2所示的规则被编码,以确定最终的操作时间($t_m$),该时间最终通过端口1传递给驾驶员模型。驾驶员模型负责使用公式(8)引导车辆沿变道轨迹行驶。
$$
y_E(t) = -\frac{6h}{t_m^5} t^5 + \frac{15h}{t_m^4} t^4 - \frac{10h}{t_m^3} t^3 \quad (8)
$$
在公式(8)中,$h$表示自车在操作结束时的最大横向位移,其值为 −3.75,即标准车道宽度。负号表示车道变换至道路右侧。
5 结果
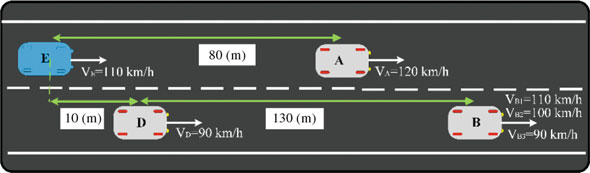
为了评估决策算法的性能,基于第3节所述场景进行了多种测试。本文展示了三种不同情况的结果并进行讨论。在情况一中,自车速度为 $v_E = 110$(km/h),车辆A以速度 $v_A = 120$(km/h)行驶,位于自车前方100(米)处。此外,车辆B和C在目标车道上分别以速度 $v_{B1} = 110$(km/h)和 $v_C = 90$(km/h)行驶,分别位于自车前方140(米)和10(米)处。在情况二和情况三中,车辆B的行驶速度分别为 $v_{B2} = 100$ 和 $v_{B3} = 90$ km/h,其余条件与情况一相同。所有说明的情况在图10中以示意图形式展示。所有情况下的轮胎‐路面摩擦等于0.9,变道操作在场景开始4.5(秒)后启动。
表4显示了基于公式1–7以及表2中的决策规则得出的最终操作时间。可以看出,对于前两个案例,决策单元允许变道操作执行。情况1的操作时间必须在3.2(秒)到4.2(秒)之间,情况2的操作时间必须在3.2(秒)到3.6(秒)之间。情况3无法执行车道变换操作。
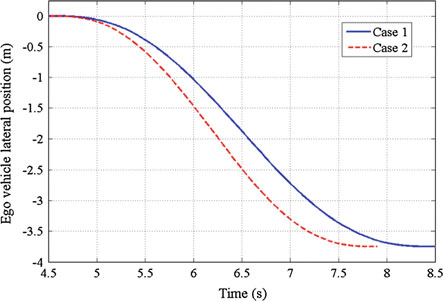
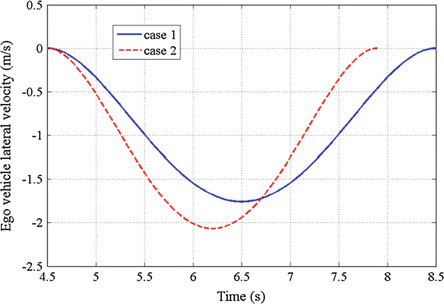
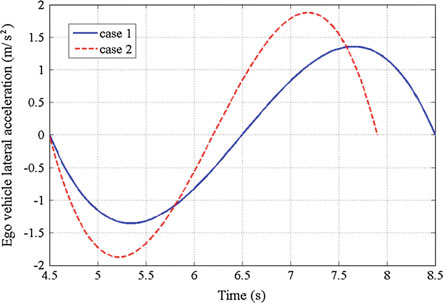
自车横向位置的示意图在图11中展示了情况一和二。此外,自车相应的横向速度和加速度分别在图12和13中给出。如图所示,在两种案例中,横向加速度值均小于2 (m/s²),满足乘客舒适性条件。
| Case | vb (m/s) | µ | t2 (s) | t3 (s) | t4 (s) | tm (s) |
|---|---|---|---|---|---|---|
| 1 | 30.6 | 0.9 | 4.2 | 1.26 | 3.2 | [3.2 4.2] |
| 2 | 27.8 | 0.9 | 3.6 | 1.26 | 3.2 | [3.2 3.6] |
| 3 | 25 | 0.9 | 3 | 1.26 | 3.2 | – |
表4 每种案例的允许的操纵时间
6 结论
本研究提出了一种用于评估新型紧急换道算法性能的方法论。该新型算法的主要优势在于考虑了道路上其他车辆的横向位置、轮胎‐路面摩擦以及实时能力。为了对所开发的算法进行性能评估,设计了一组驾驶场景,以涵盖紧急变道操作中可能出现的不同交通状况。这些场景随后在IPG CarMaker这一车辆动力学平台上实现。展示了三种不同情况的结果并进行了讨论。结果表明,该算法具有可接受的性能。




















 1909
1909

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








