bfs浅学习

看了一些关于广搜的文章，在广搜的讲解中，遇到最多的就是队列。其中会分析习题，然后写出代码，但是基本上每篇都会有含有利用c++中的学习内容，将数据压入队列中或者将队列中最前面的数据舍弃。bfs的逻辑倒是懂了，但却不知道到底应该怎么使用到bfs，这点是之后要着重学习的地方。

其实今天还是写了一道有关广搜的习题的，但是看题解还是有部分不明白。看到了一个明白一点的题解了呢又不知道这个程序哪里用了广搜。。。

先将题目和代码贴出来吧。刚刚写完代码发现调试结果是错的，今天实在忙不完了。明天打算看看是哪里出了问题，然后再给大家讲解思路和代码吧。同时进一步吧广搜弄的更加明白一些，争取自己在写题目时会用上广搜

题目：

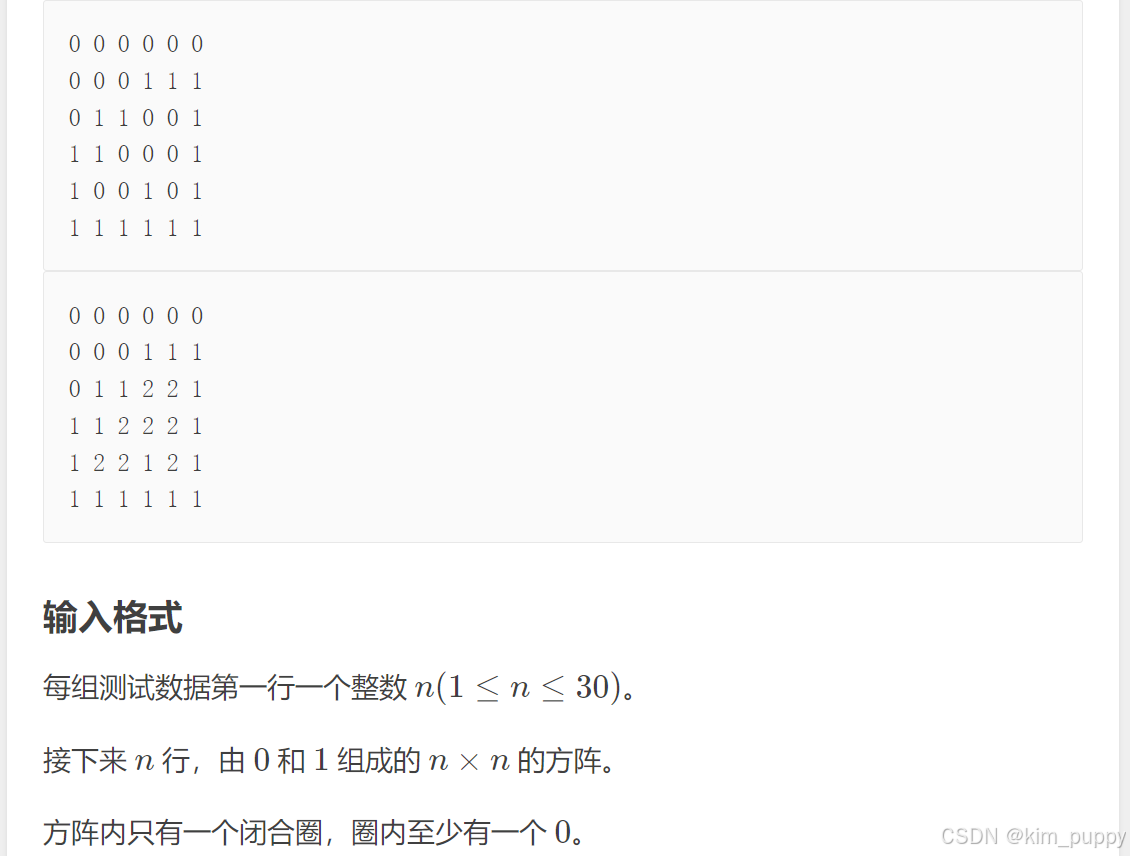
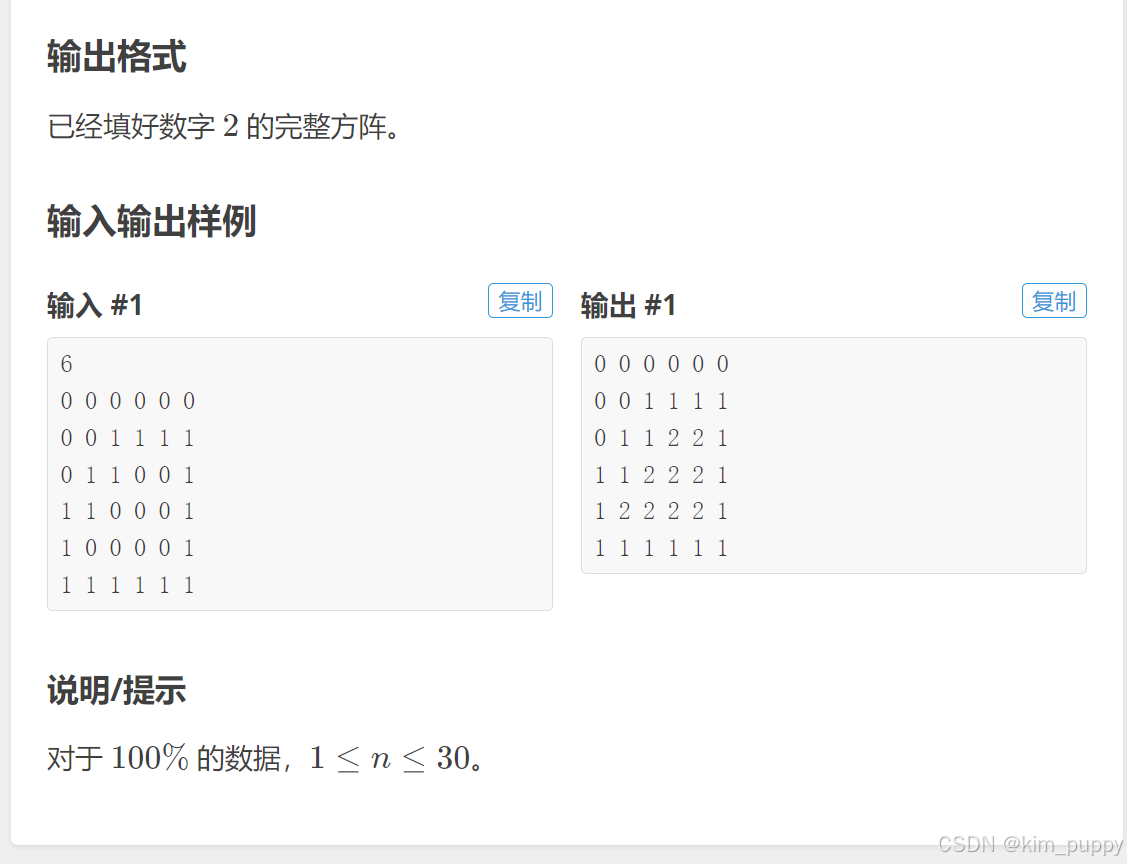
#include<stdio.h>
int main()
{
	int n = 0;
	scanf("%d", &n);//图的大小
	int map[33][33];
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= n; j++)
		{
			scanf("%d", &map[i][i]);
			if (map[i][j] == 0)
			{
				map[i][j] = 2;//先假设将所有等于0的地方涂为2，之后再找出边界外的2改为0
			}
		}
	}
	for (int i = 1; i <= n; i++)//将所有边界的2都可以置为0
	{
		map[1][i] = 0;
		map[n + 1][i] = 0;
		map[i][1] = 0;
		map[1][n + 1] = 0;
	}
	for (int i = 0; i <= n; i++)//将图扩大一圈
	{
		map[0][i] = 9;
		map[i][0] = 9;
		map[n + 1][i] = 9;
		map[i][n + 1] = 9;
	}
	for (int i = 1; i <= n; i++)
	{
		for (int j = i; j <= n; j++)
		{
			if (map[i][j] != 1)
			{
				if (map[i - 1][j] == 0 || map[i + 1][j] == 0 || map[i][j + 1] == 0 || map[i][j - 1] == 0)
				{
					map[i][j] = 0;
				}
			}
			
		}
	}
	for (int i = 0; i <= n; i++)
	{
		for (int j = 1; j <= n; j++)
		{
			printf("%d ", map[i][j]);
		}
		printf("\n");
	}
	return 0;
}

今天比较水