2024.12.08学习笔记_问题 e: 调用函数,求m-n之间的所有完数-优快云博客

1.数组练习

1.1数组练习

先是一个思路比较容易理清楚的数组问题，如下：

美国数学家维纳(N.Wiener)智力早熟，一次，他参加某个重要会议，年轻的脸孔引人注目。
于是有人询问他的年龄，他回答说：“我年龄的立方是个4位数。我年龄的4次方是个6位数。
这10个数字正好包含了从0到9这10个数字，每个都恰好出现1次。” 请你推算一下，他当时到底有多年轻。

解题思路：这道题可以将问题提供的条件拆分成两个部分，先将第一个条件执行，达到将数据范围缩小的目的，再将数据放入第二个条件进行判断，这样会清晰一些。

具体操作：利用一个for循环将满足立方是个4位数，4次方是个6位数的数求出来，这里我们说明的话就用a表示这个数。然后我们要判断是否正好包含了0到9，我这里采用的是将每个数字都提取出来，即将该数构成的4位数和6位数这十个数字通过运算结合为一个十位数，再利用取模将每个数取出来放入一个新的数组中。此时就可以让该数组的每个数依次比较，查找是否有相同的数，如果有则表示a不满足条件，反之则为正确的年龄。

话多不如代码清楚，上代码：

#include<stdio.h>
int main()
{
	int i = 1;
	int three, four;
	long long a[100];
	int num = 0;
	long long A = 0;
	int j = 0;
	int b[100];
	int f = 1;
	for (i = 1; i < 100; i++)//找出满足第一个条件的数，缩小数据范围
	{
		three = i * i * i;
		four = i * i * i * i;
		if (three >= 1000 && three <= 9999 && four >= 100000 && four < 999999)
		{
			a[f] = i;
			/*printf("%d ", a[f]);*/
			f++;
			num++;//标记有几个数满足
		}
		if (three > 9999 || four > 999999)
			break;
	}
	printf("\n");
	for (i = 1; i <= num; i++)
	{
		/*printf("%d\n", a[i]);*/
		A = a[i] * a[i] * a[i] * 1000000 + a[i] * a[i] * a[i] * a[i];//将数据合并
		for (j = 1; A > 0; j++)//将每个数字提出
		{
			b[j] = A % 10;
			A = A / 10;
			
			/*printf("%d ", b[j]);*/
		}
		/*printf("\n");*/
		for (f = 1; f < 10; f++)
		{
			for (j = f + 1; j <= 10; j++)
			{
				if (b[f] == b[j])
					break;

			}
			if (b[f] == b[j])
				break;
		}
		if (b[f] != b[j])
		{
			printf("年龄是%d", a[i]);
			break;
		}
	}

	return 0;
}

贴主在写这道题时，出现了一点问题，

有些数据的通过流程所生成的十位数在取模时，没有办法得到每个位上的数。即以下情况：

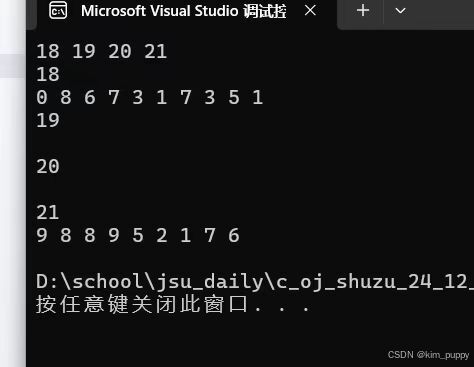
在询问大佬之后，发现是因为A的类型为int，而传递给A的数据太大了导致溢出，所以要将A改为long long类型。同时！！a数组内的元素的数据类型也要改为long long，因为在执行a[i] * a[i] * a[i] * 1000000 + a[i] * a[i] * a[i] * a[i];时，一个个逐步去乘，会将得到的数据存储在int类型中，而数据太大也会溢出，所以要将a数组改为long long。

（其实对于数组有两种改法：

1.将数组a改为直接定义为long long类型。

2.将a[i] * a[i] * a[i] * 1000000 + a[i] * a[i] * a[i] * a[i];

改为（long long）a[i] * a[i] * a[i] * 1000000 + a[i] * a[i] * a[i] * a[i];）

以上就是今天的数组学习笔记。

2.全排列的思路（运用到深搜）

2.1全排列的思路（运用到深搜）

贴主今天是第一次接触dfs，属实有点懵，下面利用全排列题目整理一下今天理解深搜的一点思路：

题目如下：

按照字典序输出自然数 1到 n 所有不重复的排列，即 n 的全排列，要求所产生的任一数字序列中不允许出现重复的数字。

思路：在处理这道题时，核心是找到全部的不重复的排列，这里使用递归函数可以解决。首先，要了解dfs的思路，我们可以将每次要用到的数看为一个节点，在一个节点时我们要继续向下寻找下一个节点，如果已经没有下一个节点，我们就将数据拿出来，这就是一种路径，接下来我们要回溯，返回上一个节点，找一找它有没有其他的下一个节点，如果没有就再次回溯到上一个节点，再次寻找该节点的其他没有使用过的节点（这里有一个点要注意，在范围上一个节点时，我们会将已使用的节点重新标记为没有使用过，这样才能找到所有情况）

（具体的解题方法和注意事项明天我会更新，因为贴主今天花了很多时间也只是将思路终于理清楚了一点点，明天会尝试敲代码，然后再分享关于深搜的更加详细的笔记）