目标检测：Generalized Focal Loss（NIPS2020）

Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection
CCF-A
Xiang Li/Wenhai Wang/Lijun Wu/Shuo Chen/Xiaolin Hu/JunLi/Jinhui Tang/Jian Yang
arXiv: Computer Vision and Pattern Recognition neural information processing systems Jun 2020

论文要解决单阶段目标检测中的两个问题：

1. 训练和推理时定位质量评估与分类分数是非一致的（ Inconsistent usage of localization quality estimation and classification score between training and inference）

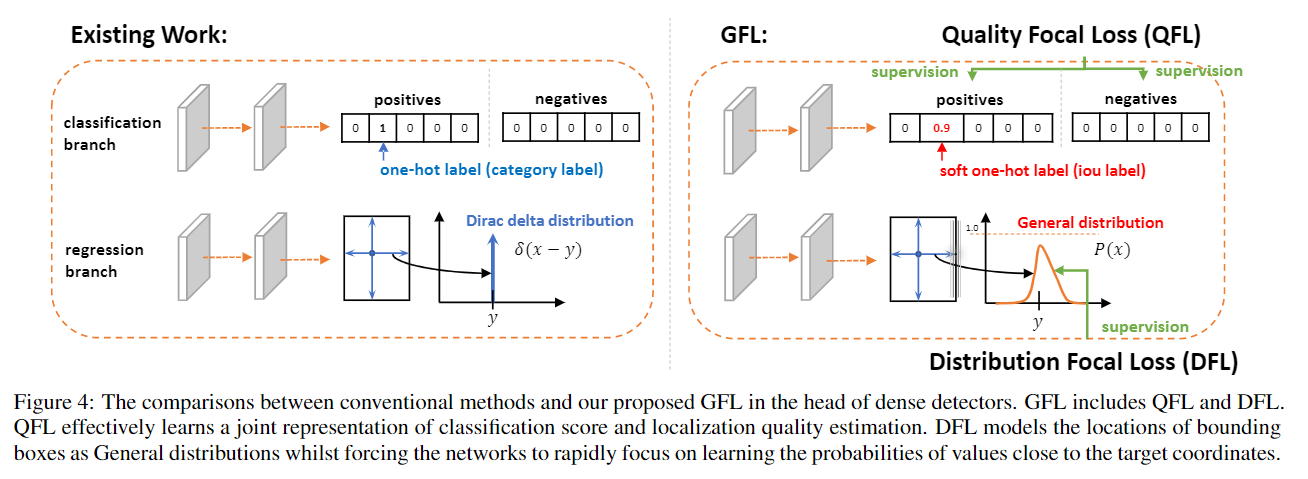
如上图左半边所示，现有方法对分类分数和iou感知分数的训练与推理策略是不一致的，这可能会导致推理时出现论文figure2中的极端情况。理论上预测的IoU很高时cls分数也应该很高（框得很准那分类判断也应该不差），反之同理。文章提出的解决办法就是将两者合并为一个统一的表达，即一个单变量。为了更有效优化这种新的表达方式，作者基于Focal loss提出了 Quality Focal Loss (QFL)。

2. 边界框的表征是不够灵活的（Inflexible representation of bounding boxes）

在边界框回归任务中，要回归的四个坐标是服从狄拉克δ分布（Dirac delta distribution）的，网络的预测结果是这分布最高概率值所对应的横坐标，但由于遮挡阴影模糊等原因，groundtruth有时并不是那么可信，即其实边界应该是一种很模糊的情况，狄拉克δ分布不能很好表示这类情况，高斯分布也是同样的问题，无法应对所有情形。
作者提议通过直接学习边界框在其连续空间中四个离散化概率分布来表示边界框位置坐标的任意分布。这样可以得到更精准更可靠的边界框估计，同时学到更多潜在的分布。进而提出了 Distribution Focal Loss（DFL），基于任意和灵活的分布下，快速并专注于学习边界框连续位置周围的概率值。作者认为边界框的概率分布应该是如下图所示的：

作者根据两个问题所提出的解决方法统称为GFL，目前听着还是比较模糊，我们沿着文章思路对这两个问题继续进行更深入的解析：

Quality Focal Loss (QFL)

如上图中QFL所示，分类分支的标签$y$是soft one-hot 标签，某类的概率值代表了该类下预测框与gt的IoU，即预测框的质量， y ∈ [0, 1]。
首先回顾Focal loss：

其中的缩放因子$(1-pt{)}^{\gamma }$在训练中自动降低简单例子的贡献，提高困难例子的比重。
作者把FL的两个部分进行了扩展, 以用于学习soft one-hot或者说连续的概率值：
（1）交叉熵部分 $-\log (p_t)$ 扩展为了 $-[(1-y)\log (1-\sigma )+y\log (\sigma )]$, 其中 σ是类别的输出概率，经sigmoid得到。可以看做是将原式做了分解加权，标签y越接近1，$\log (\sigma ))$ 的权重就越大；y越接近0，$\log (1-\sigma )$的权重就越大，两项系数和为1。
(2) 缩放因子$(1-pt)$泛化为σ到y的绝对距离，这个很好理解，FL中是σ到0或1的绝对距离。

最终得到QFL表达式如下：

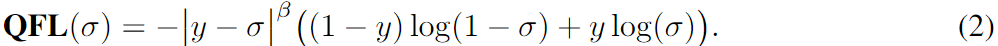
作者在对比实验中包含以下几种cls 分数表征的形式，第一种的代表应该是RetinaNet，还有YOLO v1，第二种代表就是FOCS，第三种有YOLOv2，v3，v4，v5，yolox应该也属于第三种，但多了一个obj分支。在figure7的对比实验结果中，QFL大多取得了最佳结果。总之，这个部分的改进能使得训练与推理时cls分数的产生完全一致，在NMS中能得到更好的BBox。

Distribution Focal Loss (DFL)

首先阐述传统的传统的BBox回归是将标签$y$建模为狄拉克δ分布（一个冲激函数的分布）：

$y$ 可以根据下式重建：

将分布推广到 P ( x )