单调栈--最大矩形的面积

问题：

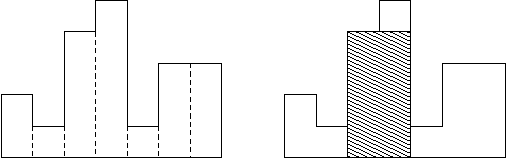
给一个直方图，求直方图中的最大矩形的面积。例如，下面这个图片中直方图的高度从左到右分别是2, 1, 4, 5, 1, 3, 3, 他们的宽都是1，其中最大的矩形是阴影部分。

input:

输入包含多组数据。每组数据用一个整数n来表示直方图中小矩形的个数，你可以假定1 <= n <= 100000. 然后接下来n个整数h1, …, hn, 满足 0 <= hi <= 1000000000. 这些数字表示直方图中从左到右每个小矩形的高度，每个小矩形的宽度为1。 测试数据以0结尾。

output:

对于每组测试数据输出一行一个整数表示答案。

sample Input：

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

sample output：

8
4000

题解：

1.我们使用单调栈来找到每一个柱形左侧和右侧第一个小于本柱形的值的坐标，应为只有其他的值大于本柱形的值，我们的矩形才能蔓延过去，如果小于本矩形的值，就不可以蔓延过去。
2.单调栈的原理是，保持栈是单调的，如果要加入的新元素不满足其单调性，就将栈中的元素弹出，知道满足单调性为止。这样，弹出的元素的第一个小于该元素的坐标就是要加入的元素的坐标。
3.对于左右就是方向相反就可。最后将每个矩形的面积计算出来，取最大的面积。复杂度为0n。

完整代码：

#include <iostream>
using namespace std;

int high[100001];
int leftl[100001];
int rightl[100001];
int thestack[100001];
/* run this program using the console pauser or add your own getch, system("pause") or input loop */

int main(int argc