（五）1.自动控制原理 Frequency Responce Methods 频率分析的基本概念

结束了时域和复域，下面我们到了频率分析的部分
介绍几个定义

频率响应：线性系统稳态正弦响应的赋值和相角随w(输入频率)变化的规律

频率特性：G(jw) = G(S)
C(jw) = G(jw) *R(jw)

幅频特性：输出信号的幅值 / 输入信号的幅值
相频特性：输出信号的三角函数的相角 - 输入信号的三角函数的相角

给出变化曲线，上面的是幅频，下面的是相频

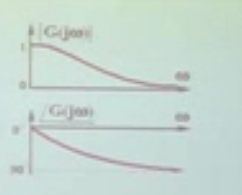
给个例题，大家就清楚是怎么简单求出一个系统的稳态正弦响应：

步骤

1.针对 传递函数，S转化为 jw 之后，求模，得到的就是 输出信号的模/ 输入信号的模
	一般输入信号已知，所以可以求到输出信号的模
2.对 传递函数 求其相角（在虚数坐标轴中找到点的位置，和原点连线的夹角）分子相角-分母相角
	例如  s/1+s 就是 jw/1+jw，相角= 90 - arctan w = 输出相角/输入相角  
	由此求出输出相角
3.写出稳态响应表达式即可

频率响应的表示方法：

1.前面说的频率特性：幅频+相频

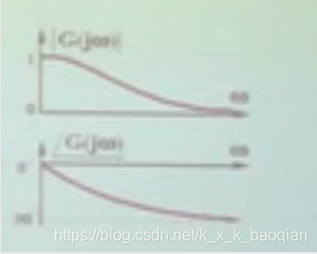
2.幅相特性：（Nyquist）
理论研究
通过 w值找到对曲线上的点，连接得到的向量，长度为幅频，与x正半轴夹角为相频
如图所示

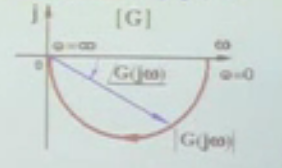
3.对数频率特性曲线：（Bode 图）
工程应用最广泛
对应的w坐标是以对数为坐标的

4.对数幅相特性： （Nichols）

对伯德图，吧w坐标省去，合并两个图，得到的就是对数幅相曲线

三个系统模型的关系：
1.微分方程
2.传递函数
3.频率特性

1.s = d/dt 得到 2.
2.中s换成jw得到3.
3.d/dt = jw得到1.