DT-RRT论文解读

论文

DT-RRT

基于Lyapunov技术的单轮车模型闭环转向控制算法

一种面向自主移动机器人的稳定跟踪控制方法

简介

传统的 RRT 算法及其改进算法仅对算法计算时间和路径代价进行了优化，普遍没有考虑到机器的运动学约束。DT-RRT 使用了双树搜索，一棵空间树和一颗状态树。空间树就是传统 RRT 算法中的树，通过采样查找可能的路径空间集合。然后在满足运动约束和动态约束的条件下，在状态树扩展得到轨迹。

提出了一种可以修改生成的树结构的重连树方案。

论文是针对两轮差速机器进行论证的。

RRT 相关算法基础在这 RRT*-Smart论文解读-优快云博客了解。

论文简述

第一节

举例了一些 RRT 的改进算法。

论文认为在动态环境中，增量规划方案比传统最优规划方案更具有优势。因为在动态未知环境中，优化轨迹不仅花费较多时间，而且轨迹也可能因为动态障碍物导致不可通行。因此最好有多个候选轨迹，以便根据实际情况选择执行。

第二节 两轮差速状态模型

这里的方程表示的是状态增量

第三节 DT-RRT

搜索父状态节点

Fig.2 实线表示空间树，实心点是空间树节点；虚线表示状态树，空心点是状态树节点

Fig.2.a 图中 α 是随机采样点，邻近点有 n0 n1 n2，其中 n2 是最近点 q_near，由 q_near 向 α 运动生成新节点 q_new。需要注意到 Fig.2.a 中的空心点，是符合机器运动学约束的状态点。

Fig.2.b 图中从邻近点 n0 n1 n2 对应的状态树节点出发向 q_new 运动生成轨迹 e0 e1 e2，轨迹终点落在 q_new 的 Er 范围内就认为机器能够抵达 q_new 节点。e2 轨迹在运动学约束内无法达到 Er，对于 e0 和 e1，e0 轨迹的时间代价比 e1 低，最后选择 e0 作为 q_new 的通道。

最后如 Fig.2.c 所示。

重新连接父节点

Fig.4 实线表示空间树，实心点是空间树节点；虚线表示状态树，空心点是状态树节点

Fig.2.a 图中在新节点 q_new 的 Br 范围内有 n0、n1 和 n2 ，其中 n0 是 q_new 的父节点，不需要考虑调整其父节点。以蓝色方块结尾的虚线表示从新节点 q_new 的状态树节点到候选节点 n1 和 n2 的成本而生成的轨迹。状态树节点 s1 的原始成本小于 e1 成本，所以 s1 不考虑把 q_new 作为父节点。状态树边的成本为 e1 > e3 > e2。

Fig.2.b 图中从节点 q_new 的状态树节点出发的 e2 的成本小于节点s2的原始成本。

Fig.2.c 图中工作空间树 n2 和状态树节点 s2 通过使用 e2 重新连接到节点 q_new。n2，s2 的原父节点 n1，s1 直接连接到 n2，s2 的子节点。

DT-RRT 的重新连接树方案维护子节点。子节点的重用有助于减少计算成本。不需要子节点的重传播操作。

机器在状态节点之间移动是需要考虑运动约束的。在 Fig.2.c 图中空间节点 n2 连接 q_new 作为父节点，n2 的原状态节点 s2 就失效了，n2 的状态节点变成了蓝色方块。从蓝色方块出发到 s2 的子节点是需要重新计算轨迹的。为了减少计算量，就保留了 e3 轨迹，原 s2 到 s2 子节点的轨迹也保留下来。空间节点 n1 直连 n2 的原子节点。

概率完整性

RRT 方案在概率上是完备的，因为如果存在路径，在迭代无穷多次后总能找到。但是在带有运动约束的状态空间中却不一定，机器在状态空间中移动是有限制的。

DT-RRT 应具有以下属性，以保证概率完整性。首先，DT-RRT 生成的每个状态节点都必须处于可行状态集，就是能够在不发生碰撞的情况下安全停车。第二个属性是必须存在两种类型的节点，即停止节点和移动节点。最后，停止节点必须能够在停止节点周围生成任意路径。

论文提到了 S. M. LaValle 和 J. J. Kuffner, Jr. 的 “Randomized kinodynamic planning” 论文，论证了随机运动学规划的概率完备性条件，但这篇论文博主看不了。

何时该生成停止节点？？？何时该生成移动节点？？？

DT-RRT 伪代码

1. 初始化空间树，插入初始节点和目标节点；

2. 初始化状态树，插入初始节点和目标节点；

3. 在限时内循环迭代：

   1. 空间树随机采样得到 q_rand 节点

   2. 根据采样点 q_rand 扩展空间树，获得向采样点的最近节点 q_near，由 q_near 到 q_rand 生成的 q_new 节点，以及节点类型（移动节点，停止节点）

   3. 搜索父状态节点(看前面小节)

   4. 如果找不到父状态节点，跳过下面步骤进入下次迭代

   5. 空间树更新节点

   6. 状态树更新节点

   7. 重新连接父节点(看前面小节)

4. 结束循环

5. 返回树

第四节 重新规划算法

这部分是对第三节规划完成后的 DT-RRT 的重新规划，用之前保存下来的空间树和状态树，根据机器的当前状态再次复用规划。下面提到到了“新障碍物”，“更新根节点” 这类像是局部规划才会涉及到内容。但是在伪代码部分又不会有新的采样，所以这部分功能究竟是在哪里使用呢？？？

更新目标轨迹并删除不可达节点

Fig.5 碰撞检测删除节点示意图

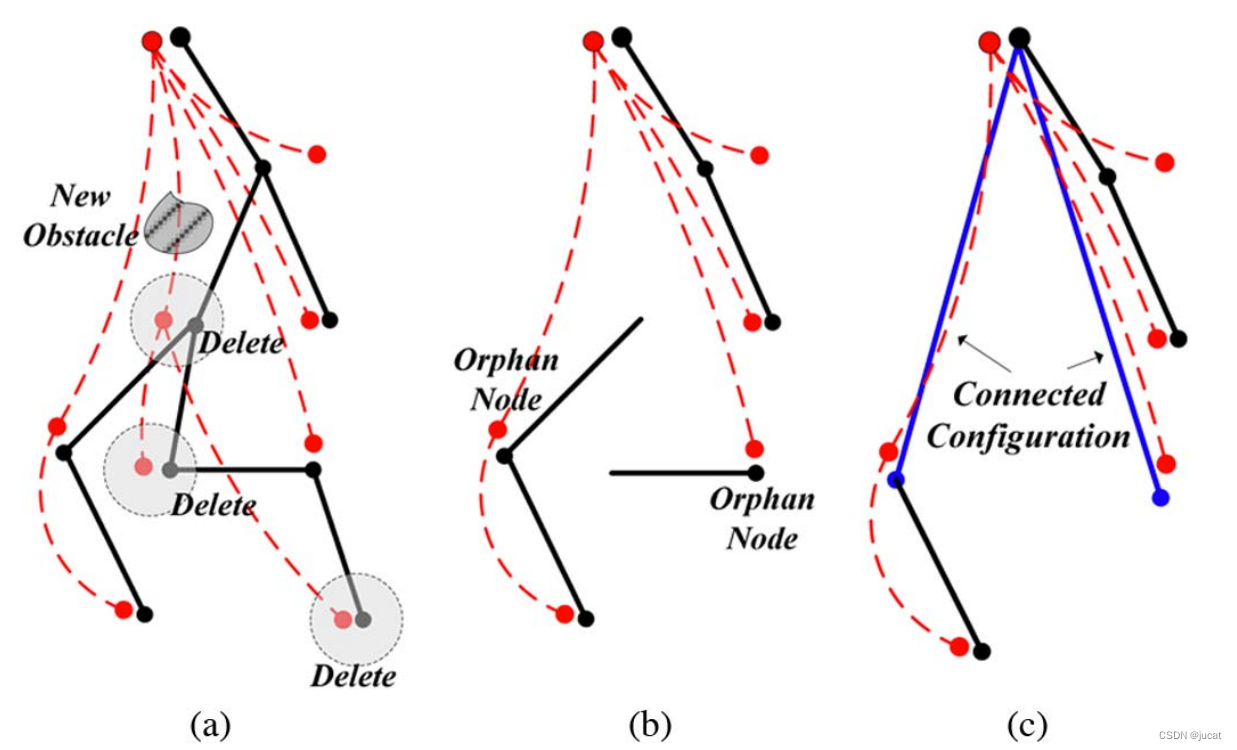
Fig.5.a 图中，一个新的障碍物阻挡了轨迹（红色节点和红色虚线），该障碍物后面的子空间节点和子状态节点被标记为要删除。

Fig.5.b 图中删除了标记的节点。

Fig.5.c 由于空间树和状态树可能具有不同的父节点，因此应连接孤立节点（蓝色线段），图中孤立节点的父节点由状态树确定。

整理树分支

Fig.6 重新规划时候的分支处理

必须删除未从目标状态启动的不可行节点。

Fig.6.a 图中，当机器跟踪轨迹（从顶点红色节点到 NewStateRoot 节点的虚线）离开了顶点红色状态节点后，选择 NewStateRoot 作为新的根节点重新规划。原来状态树中不是来自 NewStateRoot 的其他状态节点要被标记删除。

Fig.6.b 图中删除了标记的节点。

Fig.6.c 图中连接孤立节点（蓝色线段）。根轨迹沿着恒定的长度被分割，插入新状态节点（SegmentRootNode 和 RootNode）。

重新规划算法伪代码

1. 将机器当前状态 x_cur 代入空间树 TW，状态树 TX 中更新位置

2. 在 FindTrajectory(TX) 函数中，会对状态空间下的轨迹进行碰撞检查，搜索代价最低的轨迹

3. 如果找不到轨迹返回空

4. 整理树分支

5. 获取代价最低的轨迹

6. 返回轨迹

第五节 仿真实验结果

看仿真的图 DT-RRT 的采样好像不是随机的，emmm

仿真实验配置

a 图：机器； b 图：仿真环境

仿真结果

无障碍物环境仿真 100 条路径 a 图：RRT； b 图：DT-RRT

有障碍物环境仿真 100 条路径 a 图：RRT；b 图：DT-RRT

窄通道仿真 100 条路径 a 图：RRT；b 图：DT-RRT

真实环境测试 30 条路径 a 图：RRT；b 图：DT-RRT

第六节 结论

为两轮移动机器人的动态轨迹规划设计的 DT-RRT 算法可以降低规划轨迹的计算成本。实验结果表明，移动机器人能够准确地跟踪使用DT-RRT生成的轨迹。

附录 用于生成轨迹的边类型和运动控制器

边类型

机器的状态节点要么处于零速度的停止状态，要么处于非零速的移动状态。停止状态允许机器在狭窄或杂乱环境中原地旋转。这两种状态节点类型组合可以得到 4 种边类型

a：停止-停止；b：停止-移动；c：移动-移动；d：移动-停止黑色实线圆点是空间树及节点；红色虚线圆点是状态树及节点

图 a：在起始停止节点，机器原地旋转朝向子停止节点，直线运动过去，然后停止；

图 b：在起始停止节点，机器原地旋转朝向子移动节点，按运动约束移动到子节点；

图 c：在起始移动节点，机器按运动约束移动到子移动节点；

图 d：在起始移动节点，机器按运动约束移动到子停止节点，然后停止；

控制器方案

Fig.21 a：终点停止的轨迹规划算法；b：无终点条件的轨迹规划算法

终点停止的轨迹算法

该控制算法原理详情看原论文，基于Lyapunov技术的单轮车模型闭环转向控制算法

Fig.21.a 中，ρ 是机器与终点的欧氏距离，θ 是机器当前航向角与终点节点航向角的角度差，γ 是当前机器转向终点节点的角度，δ 是终点节点航向角调整角度（机器抵达终点后，最后再调整角度），k1 k2 k3 是增益参数。

从公式 (3) 可以看到抵达终点后，ρ 减小到 0，线速度也为 0；

贴几张该控制算法原论文图片

初始位置机器航向角与终点航向角一致

初始位置机器航向角与终点航向角差90°

无终点条件的轨迹算法

该控制算法原理详情看原论文，一种面向自主移动机器人的稳定跟踪控制方法

Fig.21.b 中，qr 是参考点（目标点）qc 是当前位姿点，qe 是 qc 到 qe 的转换偏置。u 是线速度和角速度增量，

v_max 是参考点 qr 位置的速度，应该说是目标速度才对。控制增益 kx、ky 和 kθ 是正实数，会影响收敛特性。

根据节点之间的边类型，使用公式(3)或(5)可计算出在无加速度约束的情况下的可靠轨迹。

如果控制器与加速度约束一起使用，则生成的轨迹可能不会收敛到目标位置。