通信原理_2 确定信号分析

内积公式

$$E_{xy}=<x,y>={\int }_{-\infty }^{+\infty }{x}^{\ast }(t)y(t)dt$$

能量用内积的解释

信号与其自身的内积就是能量。

$$E_x={\int }_{-\infty }^{+\infty }|x(t{)}^2|dt={\int }_{-\infty }^{+\infty }|X(f){|}^{2}df={\int }_{-\infty }^{+\infty }x(t)x^{\ast }(t)dt={\int }_{-\infty }^{+\infty }X(f)X^{\ast }(f)df$$

(帕瑟瓦尔定理：用时域或频域求内积都能得到能量。${\int }_{-\infty }^{+\infty }|x(t){|}^{2}dt={\int }_{-\infty }^{+\infty }|X(f){|}^{2}df$)

内积为0：信号正交。

两个信号相加的能量=各自能量+互能量=$E_x+E_y+E_{xy}+E_{yx}$

许瓦兹不等式

许瓦兹不等式就是说互能量的范围。互能量的模值<=自能量乘积开方。

由能量式可以推出：

$$|{\int }_{-\infty }^{+\infty }x(t)y^{\ast }(t)dt|=E_{xy}\le \sqrt{E_x{E}_y}$$

当y(t)=K·x(t)时，即两个信号波形相同时，其内积最大。

时域内积=频域内积

${\int }_{-\infty }^{+\infty }{x}^{\ast }(t)y(t)dt={\int }_{-\infty }^{+\infty }{X}^{\ast }(f)Y(f)df$

内积=0被称为信号正交，时域正交时频域也正交。正交的两个信号，信号相加的能量=各自的自能量直接相加，因为互能量=0.

能量归一化

能量归一化：$\frac{x(t)}{\sqrt{E_x}}$ 的能量=1.

归一化相关系数$$

相关系数=1：y(t)是x(t)的倍数关系。

=0：y(t)中不包含x(t)。

0~1：y(t)由一部分x(t)和一部分x(t)的正交组成。

相关函数

$R_{xy}(\tau )={\int }_{-\infty }^{+\infty }x(t+\tau )y^{\ast }(t)dt$

注意顺序。当然实信号的话加不加星号并无影响。

相关函数$\le \sqrt{E_x{E}_y}$。

$R_{xy}(\tau )=R_{yx}^{\ast }(-\tau )$

因此自相关函数共轭偶对称：$R_x(\tau )=R_x^{\ast }(-\tau )$当然实信号可以去掉*，说明实信号的自相关函数是偶函数。

tau=0时的自相关函数就是自能量，互相关函数就是互能量。此时相关函数取最大值。

相关函数$\le \sqrt{P_x{P}_y}$。

功率信号\tau=0时相关函数=功率。

能量谱密度和功率谱密度

能量有限时，可以考虑x(t)的能量谱密度。

时域内积=频域内积

$E_x={\int }_{-\infty }^{+\infty }|x(t){|}^{2}dt={\int }_{-\infty }^{+\infty }|X(f){|}^{2}df$

因此可以把下式称为能量谱密度：

$E_x(f)=|X(f){|}^2$

而互能量谱密度即为$E_{yx}(f)=Y(f)X^{\ast }(f)$

相关函数的傅氏变换是能量谱密度。求自相关函数不好求的时候可以用频域能量谱密度返回去。

$E_x(f)=|X(f){|}^2={\int }_{-\infty }^{+\infty }{R}_x(\tau )e^{-j2\pi f\tau }d\tau$

功率：对相关函数的求平均值。

tau=0：互相关/自相关函数的功率。

根据许瓦兹不等式可以推出：互相关函数的功率<各自的功率的开根的乘积。

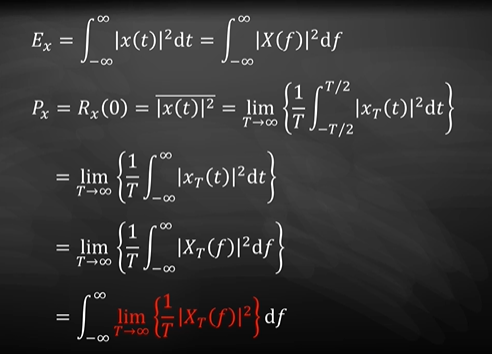
可以推出：功率谱密度 P x ( f ) = l i m T → ∞ { 1 T ∣ X T ( f ) 2 ∣ d f } P_x(f)=lim_{T→\infty}\{\frac{1}{T}|X_T(f)^2|df\} Px​(f)=limT→∞​{T1​∣XT​(f)2∣df}

P x y ( f ) = l i m T → ∞ { 1 T X T ( f ) Y T ∗ ( f ) d f } P_{xy}(f)=lim_{T→\infty}\{\frac{1}{T}X_T(f)Y_T^*(f)df\} Pxy​(f)=limT→∞​{T1​XT​(f)YT∗​(f)df}

功率谱密度也可以通过自相关函数求傅氏变换得到。

单边谱密度

工程上常用单边谱密度，即把f<0和f>0的部分折合到一起，只考虑f>0的部分。

$P_x^{单}(f)=P_x(f)+P_x(-f)$

求功率的话只求0~+无穷的部分即可。

单边谱密度定义域只有[0, +无穷)，不是说(-无穷,0]的部分是=0！画图时注意只画正半轴。

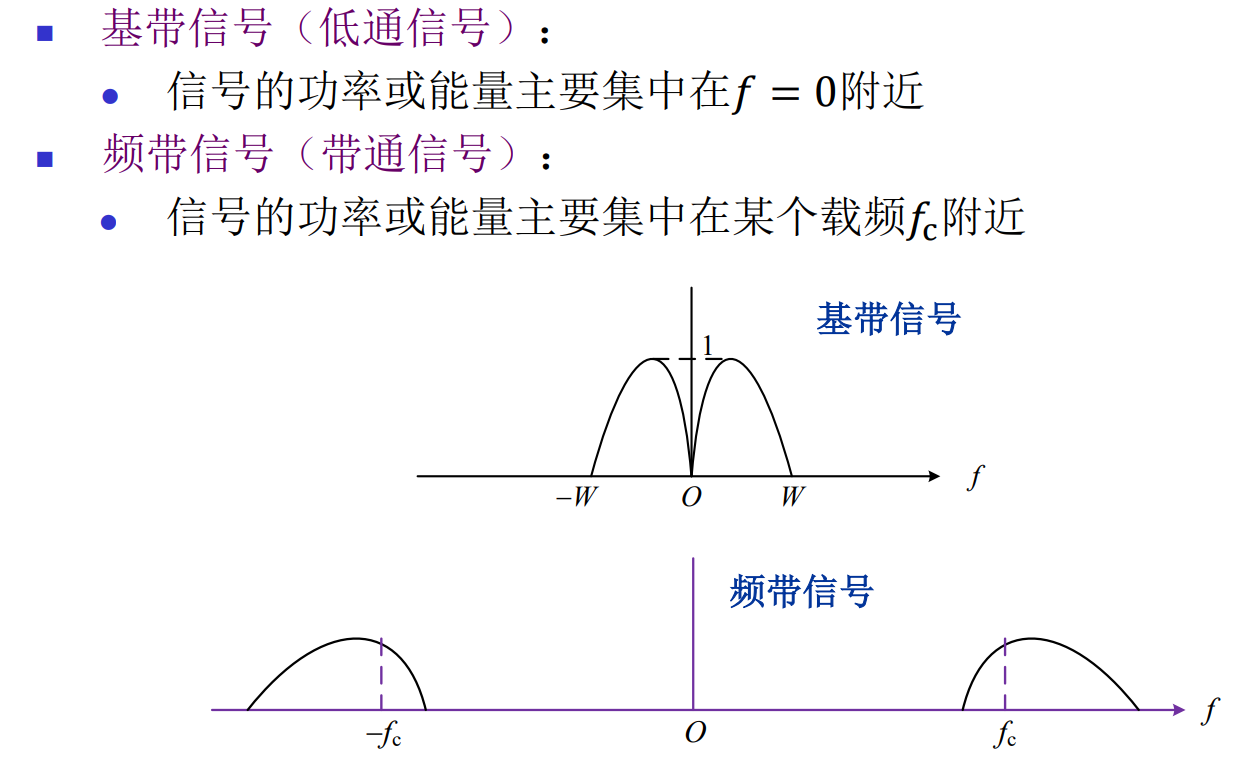
带宽

单边谱的频谱宽度

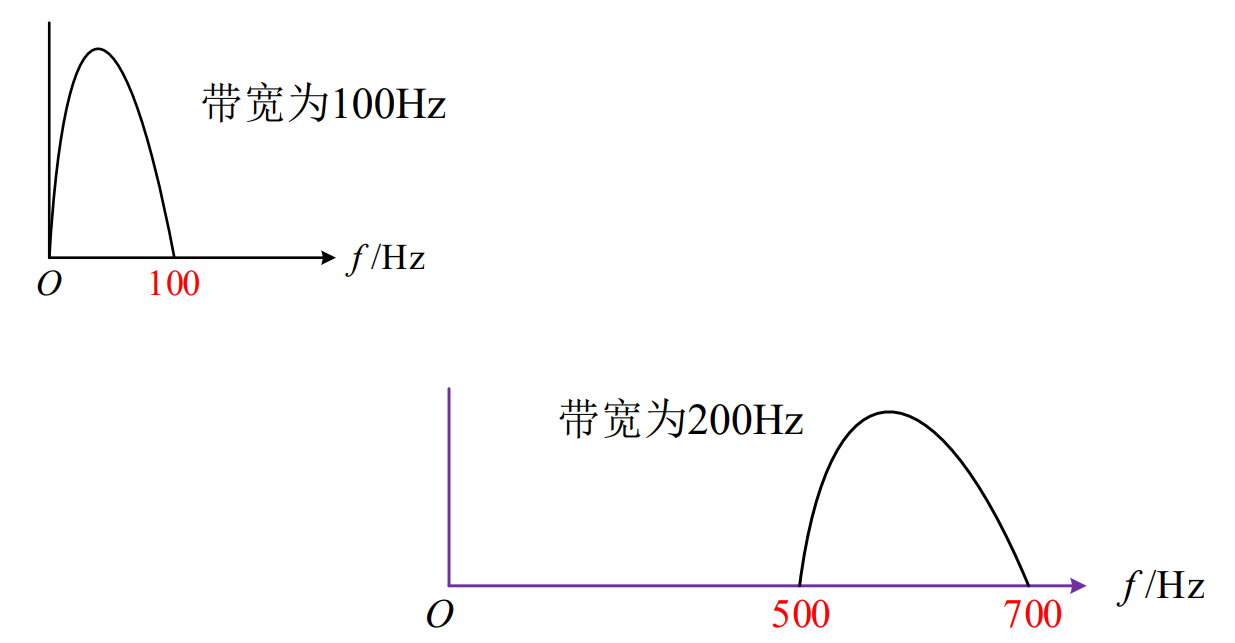
主瓣带宽

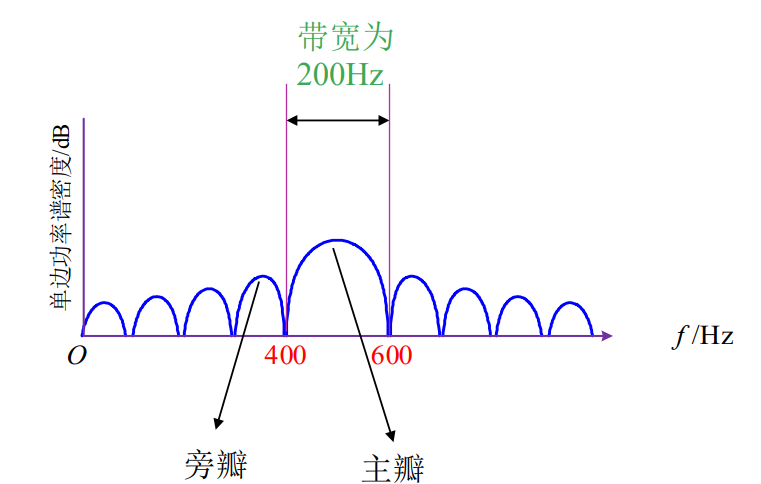
3dB带宽

等效矩形带宽

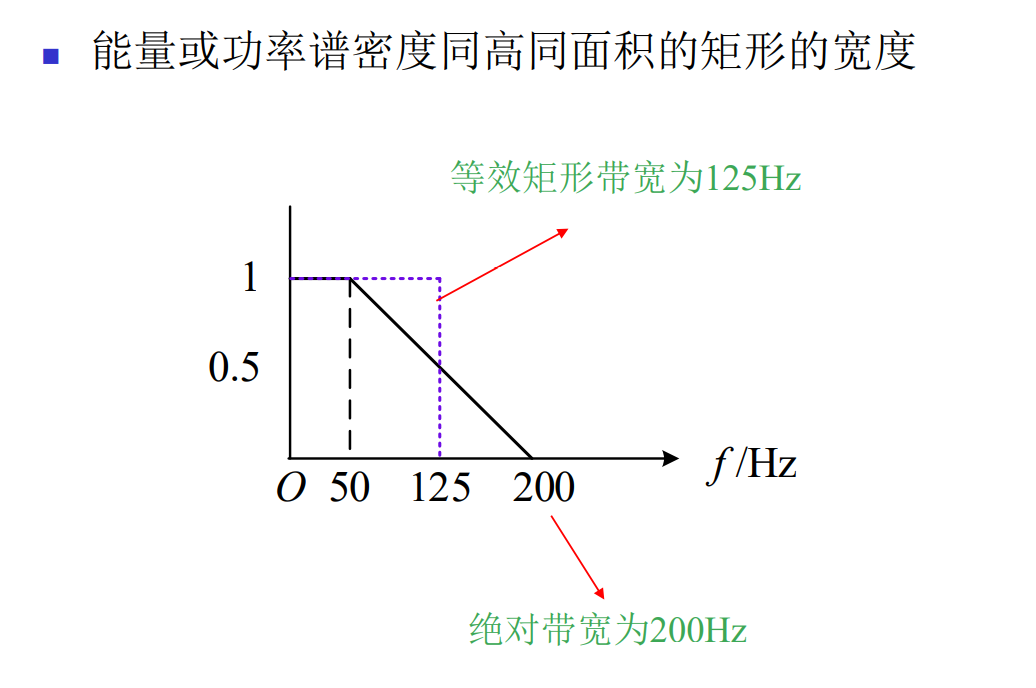
按能量占比定义的带宽

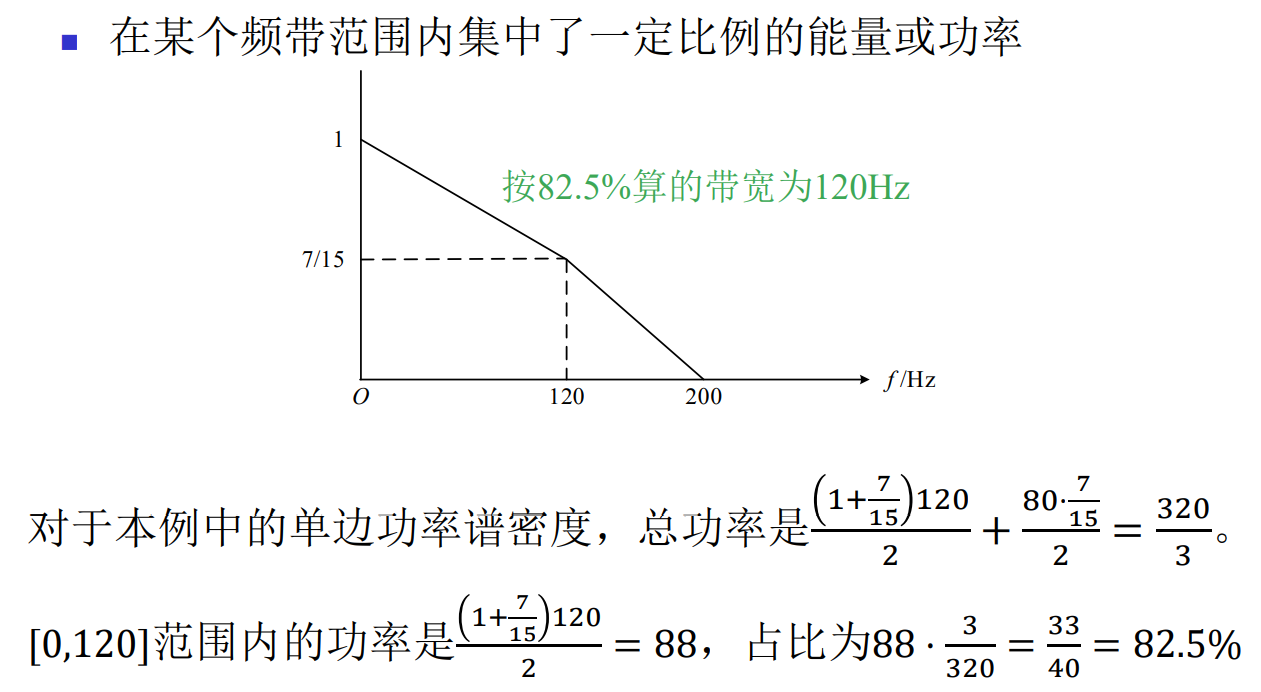
信号平方的带宽

信号带宽是W，信号平方带宽是2W。

正弦调制信号

实基带信号 x(t) 的绝对带宽是 W。

$s(t)=x(t)cos2\pi f_{c}t(f_c>W)$ 的绝对带宽是 2W。

线性时不变系统

时域卷积=频域乘积。

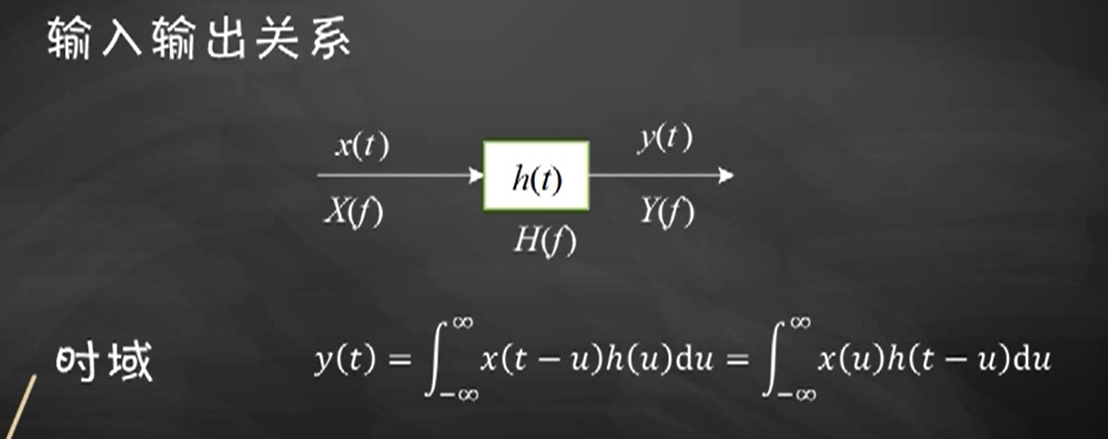
H(f) 被称作传递函数。

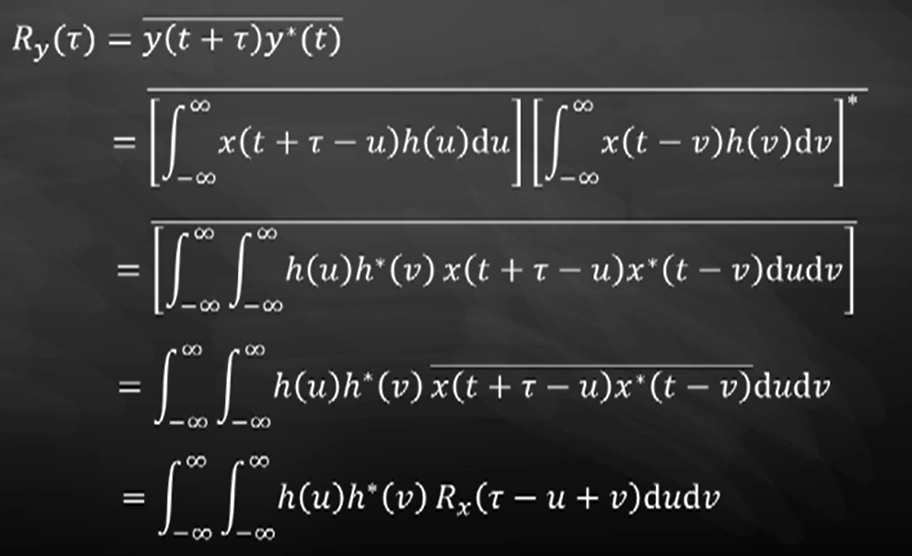
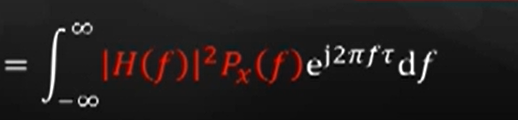
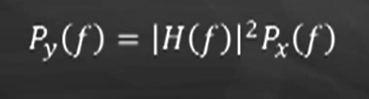
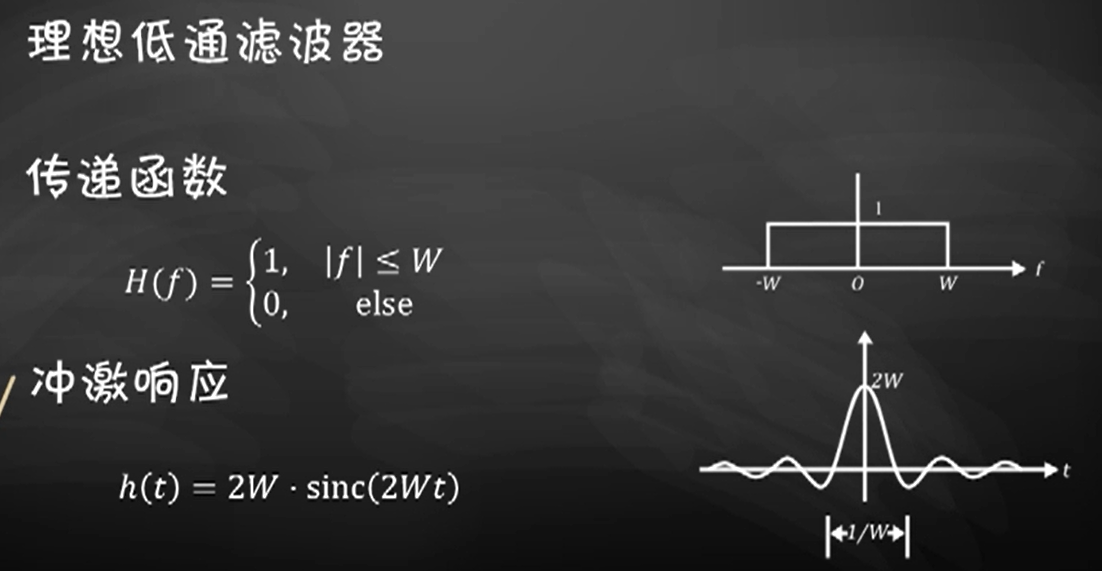
希尔伯特变换

x(t) 通过一个特殊的 h(t) 变换为 $\hat{x}(t)$ ，被称作希尔伯特变换。

这个 h(t) 如下：

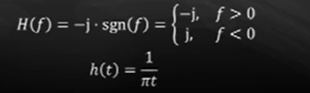
因为 H(f) 的模值=1，所以希尔伯特变换不影响能量谱/功率谱密度和自相关函数。

奇函数偶函数经过希尔伯特变换变为偶函数/奇函数。

$x(t)$ 和 $\hat{x}(t)$ 正交。即两者乘积的积分=0。

解析信号：$z(t)=x(t)+j\hat{x}(t)$.

由x(t)→z(t) 的传递函数 H(f)：=2 (f>0); =0 (f<0)。

因此 Z(f) 就是 X(f) 正半轴*2，负半轴*0.

$m(t)cos2\pi f_{c}t$ 的希尔伯特变换是 $m(t)sin2\pi f_{c}t$。$z(t)=m(t)e^{j2\pi f_{c}t}$.

带通信号的复包络

带通信号是什么？

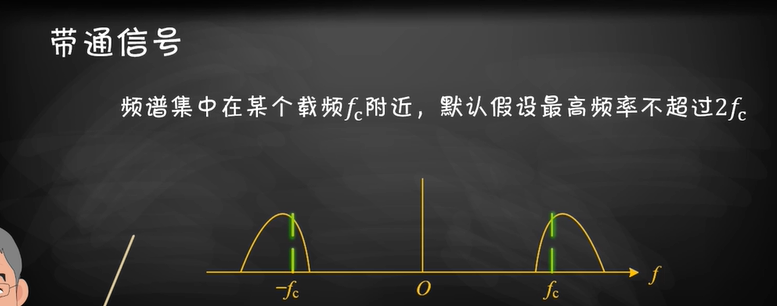
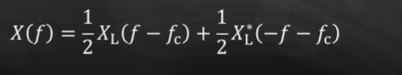
带通信号的表示

从复包络的频谱反推出带通信号x(t)的频谱有三种：

x ( t ) = R e { x L ( t ) e j 2 π f c t } x(t)=Re\{x_L(t)e^{j2\pi f_ct}\} x(t)=Re{xL​(t)ej2πfc​t}

$x(t)=x_c(t)cos2\pi f_{c}t-x_s(t)sin2\pi f_{c}t$

$x(t)=A(t)cos[2\pi f_{c}t+\varphi (t)]$

复包络：

$x_L(t)=[x(t)+j\hat{x}(t)]e^{-j2\pi f_{c}t}$

$x_L(t)=x_c(t)+j{x}_s(t)$

$x_L(t)=A(t)e^{j\varphi (t)}$

相位$\varphi (t)=ta{n}^{-1}\frac{x_s(t)}{x_c(t)}$

带通系统的等效基带分析

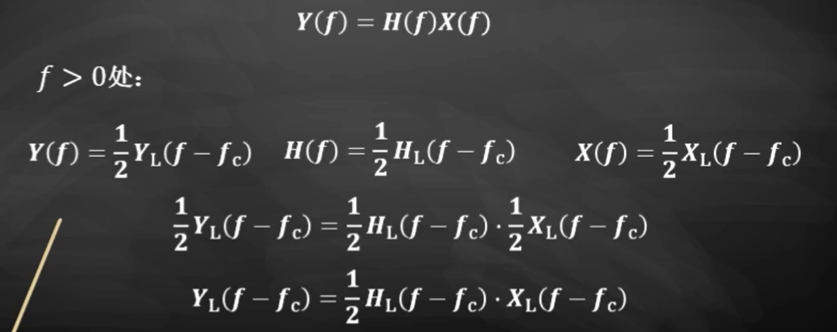
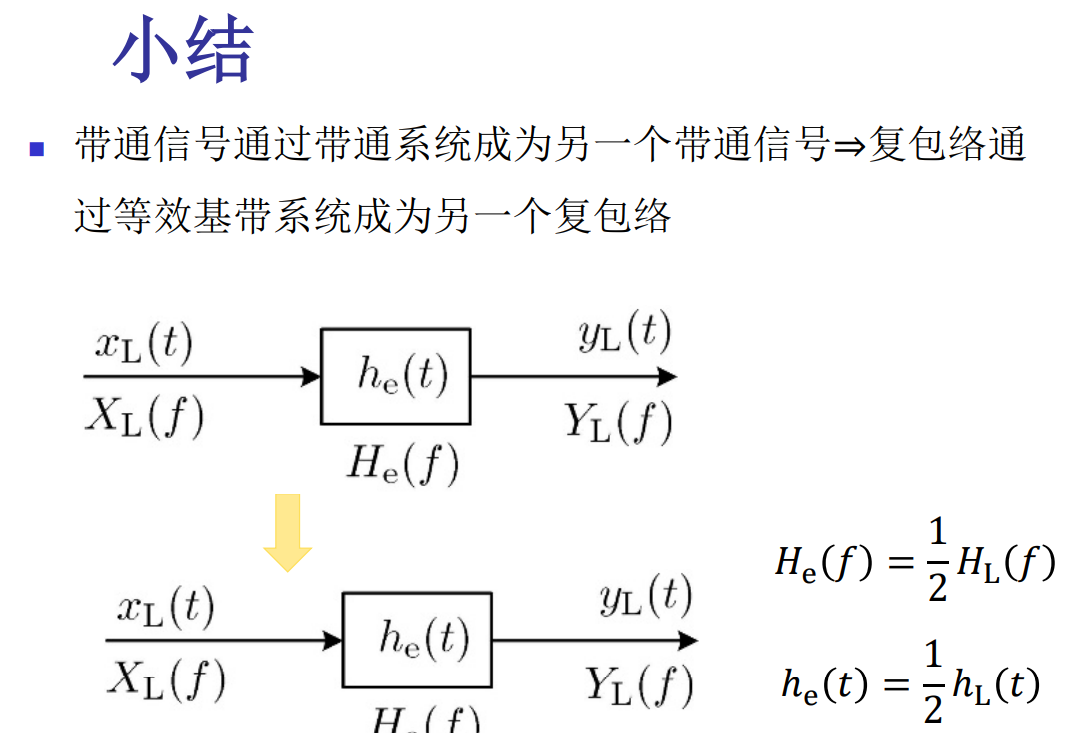
可以先通过：

$Y(f)=X(f)H(f)$

$Y_L(f)=X_L(f)H_e(f)$

$H_e(f)=\frac{1}{2}{H}_L(f)$

这样碰到比较难积分的Y的时候，可以先转化成YL(f)，再通过带通信号的表示转化回来。