为什么线性回归的损失函数采用均方误差？——基于最大似然估计的深度解析_优化均方误差损失等价于最大化高斯分布的似然函数吗-优快云博客

本文链接：https://blog.youkuaiyun.com/jsntghf/article/details/148512051

在机器学习领域，线性回归是最基础且广泛应用的算法之一。当我们初次学习线性回归时，通常会被告知要通过“最小化平方误差”来训练模型。但一个自然的问题是：为什么偏偏选择平方误差？许多函数都可以衡量预测值与真实值之间的差异，为什么平方误差成为标准选择？本文将从概率论的角度，通过严密的数学推导，揭示均方误差在线性回归中使用的深层原因（扩展阅读：不会选损失函数？16种机器学习算法如何“扣分”？-优快云博客、10 个最常用的损失函数-优快云博客）。

线性回归模型的基本设定

首先，我们形式化线性回归模型。给定输入特征 $X \in \mathbb{R}^n$ 和目标变量 $y \in \mathbb{R}$ ，线性回归模型表示为：

$y = \theta^T X + \epsilon$

其中：

$\theta$ 是模型参数向量
$\epsilon$ 是误差项，捕捉模型无法解释的随机噪声

噪声分布的关键假设

为了从概率角度理解平方误差的由来，我们需要对噪声项 $\epsilon$ 做出分布假设。根据中心极限定理，大量独立随机变量的和趋向于服从高斯分布，因此我们合理假设：

$\epsilon \sim \mathcal{N}(0, \sigma^2)$

即噪声服从均值为0、方差为 $\sigma^2$ 的高斯分布。这意味着：

$p(\epsilon_i) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{\epsilon_i^2}{2\sigma^2}\right)$

从噪声分布到条件概率

将 $\epsilon_i = y_i - \theta^T X_i$ 代入，我们得到在给定参数 $\theta$ 和输入 $X_i$ 下观测到 $y_i$ 的概率：

$p(y_i | X_i; \theta) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(y_i - \theta^T X_i)^2}{2\sigma^2}\right)$

这表明在参数 $\theta$ 下， $y_i$ 服从均值为 $\theta^T X_i$ 、方差为 $\sigma^2$ 的正态分布。

似然函数的构建

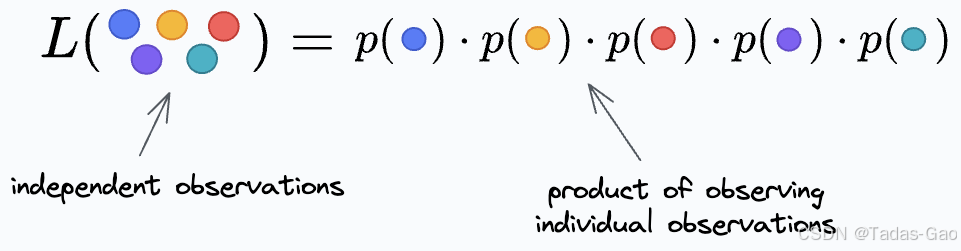
对于独立同分布的 $m$ 个观测数据，联合似然函数是所有单个数据点概率的乘积：

$\begin{aligned} L(\theta) &= p(\vec{y} | X; \theta) \\ &= \prod_{i=1}^m p(y_i | X_i; \theta) \\ &= \prod_{i=1}^m \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(y_i - \theta^T X_i)^2}{2\sigma^2}\right) \end{aligned}$

对数似然及简化

为了计算方便，我们通常最大化对数似然函数（因为对数函数是单调递增的，最大化对数似然等价于最大化似然）：

$\begin{aligned} \ell(\theta) &= \log L(\theta) \\ &= \sum_{i=1}^m \log \left[ \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(y_i - \theta^T X_i)^2}{2\sigma^2}\right) \right] \\ &= \sum_{i=1}^m \left[ \log \frac{1}{\sqrt{2\pi\sigma^2}} - \frac{(y_i - \theta^T X_i)^2}{2\sigma^2} \right] \\ &= m \log \frac{1}{\sqrt{2\pi\sigma^2}} - \frac{1}{2\sigma^2} \sum_{i=1}^m (y_i - \theta^T X_i)^2 \end{aligned}$

最大似然估计与平方误差的关系

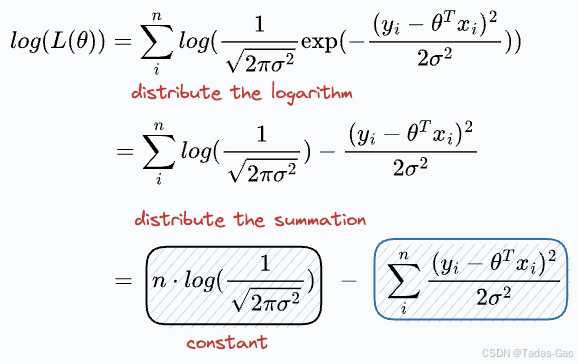
我们的目标是找到参数 $\theta$ 使得对数似然函数 $\ell(\theta)$ 最大化。观察上式：

第一项 $m \log \frac{1}{\sqrt{2\pi\sigma^2}}$ 是与 $\theta$ 无关的常数
第二项中的分母 $2\sigma^2$ 是正常数，不影响优化方向
因此，最大化 $\ell(\theta)$ 等价于最小化 $\sum_{i=1}^m (y_i - \theta^T X_i)^2$

这正是均方误差（MSE）的定义：

$J(\theta) = \frac{1}{m} \sum_{i=1}^m (y_i - \theta^T X_i)^2$

常见误解的澄清

平方误差是可微分的：虽然确实可微，但这只是平方误差的一个性质而非根本原因。绝对误差也有其对应的光滑近似（如Huber损失）。
对大误差惩罚更大：这解释了平方误差的一个效果，但没说明为什么这种惩罚方式是理论上最优的。

通过最大似然框架，我们看到了平方误差不是任意选择的，而是在高斯噪声假设下的自然结果。

高斯假设的合理性

你可能会问：如果噪声不是高斯分布呢？确实，这时最小二乘可能不是最优方法：

对于重尾分布，使用绝对误差或Huber损失更鲁棒
对于分类问题（输出为概率），交叉熵损失更合适

但在许多实际应用中，中心极限定理为高斯噪声假设提供了合理基础，这使得最小二乘法成为线性回归的自然选择。

代码演示：线性回归损失函数与最大似然估计的关系

下面我将通过Python代码演示为什么线性回归采用均方误差作为损失函数，以及这与最大似然估计之间的关系。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# 设置随机种子以便复现结果
np.random.seed(42)

# 1. 生成模拟数据
# 真实参数：w=2, b=1
true_w = 2.0
true_b = 1.0

# 生成100个在[0,1]区间均匀分布的x值
x = np.linspace(0, 1, 100)
# 生成带有高斯噪声的y值 (噪声标准差sigma=0.2)
noise = np.random.normal(0, 0.2, size=x.shape)
y = true_w * x + true_b + noise

# 设置支持中文的字体
#plt.rcParams['font.sans-serif'] = ['SimHei']  # Windows
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']  # macOS
#plt.rcParams['font.sans-serif'] = ['WenQuanYi Zen Hei']  # Linux

# 解决负号显示问题
plt.rcParams['axes.unicode_minus'] = False  

# 可视化生成的数据
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.scatter(x, y, label='观测数据')
plt.plot(x, true_w*x + true_b, 'r-', label='真实关系')
plt.xlabel('x')
plt.ylabel('y')
plt.title('生成的数据和真实关系')
plt.legend()

# 2. 展示不同参数下的拟合情况
# 定义一些可能的w和b值
w_vals = np.linspace(1.5, 2.5, 5)
b_vals = np.linspace(0.5, 1.5, 5)

# 计算不同参数组合的均方误差(MSE)
mse_values = np.zeros((len(w_vals), len(b_vals)))
for i, w in enumerate(w_vals):
    for j, b in enumerate(b_vals):
        y_pred = w * x + b
        mse = np.mean((y - y_pred)**2)
        mse_values[i, j] = mse

# 找到MSE最小的参数组合
min_idx = np.unravel_index(np.argmin(mse_values), mse_values.shape)
best_w = w_vals[min_idx[0]]
best_b = b_vals[min_idx[1]]

# 可视化MSE曲面
W, B = np.meshgrid(w_vals, b_vals)
plt.subplot(1, 2, 2, projection='3d')
plt.gca().plot_surface(W, B, mse_values.T, cmap='viridis', alpha=0.8)
plt.scatter([best_w], [best_b], [mse_values.min()], color='red')
plt.xlabel('w')
plt.ylabel('b')
plt.title('MSE损失函数曲面\n红点:最小MSE点')
plt.tight_layout()
plt.show()

# 3. 展示最大似然估计与MSE的关系
def likelihood(w, b, sigma=0.2):
    """计算给定参数下的对数似然值"""
    y_pred = w * x + b
    # 计算每个数据点在正态分布下的概率密度对数
    log_probs = norm.logpdf(y, loc=y_pred, scale=sigma)
    return np.sum(log_probs)

# 计算不同参数组合的对数似然值
ll_values = np.zeros((len(w_vals), len(b_vals)))
for i, w in enumerate(w_vals):
    for j, b in enumerate(b_vals):
        ll_values[i, j] = likelihood(w, b)

# 找到最大似然的参数组合
max_idx = np.unravel_index(np.argmax(ll_values), ll_values.shape)
best_w_ll = w_vals[max_idx[0]]
best_b_ll = b_vals[max_idx[1]]

print(f"通过最小化MSE得到的最佳参数: w={best_w:.3f}, b={best_b:.3f}")
print(f"通过最大化似然得到的最佳参数: w={best_w_ll:.3f}, b={best_b_ll:.3f}")

# 4. 展示MSE和负对数似然的关系
sigma = 0.2  # 使用真实的噪声标准差
n = len(y)   # 样本数量

# 计算负对数似然 (忽略常数项)
def neg_log_likelihood(w, b):
    y_pred = w * x + b
    return (1/(2*sigma**2)) * np.sum((y - y_pred)**2)

# 比较MSE和负对数似然的关系
print("\nMSE和负对数似然的关系:")
print(f"当w={true_w}, b={true_b} (真实参数):")
print(f"MSE: {np.mean((y - (true_w*x + true_b))**2):.4f}")
print(f"负对数似然: {neg_log_likelihood(true_w, true_b):.4f}")

print(f"\n当w={best_w}, b={best_b} (最小MSE参数):")
print(f"MSE: {np.mean((y - (best_w*x + best_b))**2):.4f}")
print(f"负对数似然: {neg_log_likelihood(best_w, best_b):.4f}")

# 5. 可视化MSE和负对数似然的关系
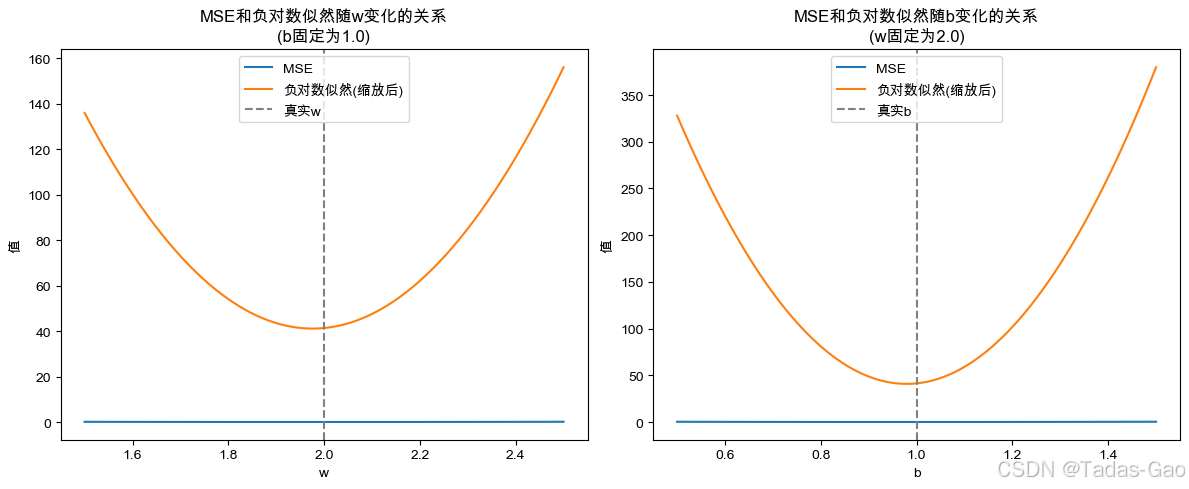
plt.figure(figsize=(12, 5))

# 固定b=1，变化w，观察MSE和负对数似然
w_range = np.linspace(1.5, 2.5, 100)
fixed_b = 1.0
mse_list = [np.mean((y - (w*x + fixed_b))**2) for w in w_range]
nll_list = [neg_log_likelihood(w, fixed_b) for w in w_range]

plt.subplot(1, 2, 1)
plt.plot(w_range, mse_list, label='MSE')
plt.plot(w_range, nll_list, label='负对数似然(缩放后)')
plt.axvline(true_w, color='gray', linestyle='--', label='真实w')
plt.xlabel('w')
plt.ylabel('值')
plt.title('MSE和负对数似然随w变化的关系\n(b固定为1.0)')
plt.legend()

# 固定w=2，变化b，观察MSE和负对数似然
b_range = np.linspace(0.5, 1.5, 100)
fixed_w = 2.0
mse_list = [np.mean((y - (fixed_w*x + b))**2) for b in b_range]
nll_list = [neg_log_likelihood(fixed_w, b) for b in b_range]

plt.subplot(1, 2, 2)
plt.plot(b_range, mse_list, label='MSE')
plt.plot(b_range, nll_list, label='负对数似然(缩放后)')
plt.axvline(true_b, color='gray', linestyle='--', label='真实b')
plt.xlabel('b')
plt.ylabel('值')
plt.title('MSE和负对数似然随b变化的关系\n(w固定为2.0)')
plt.legend()

plt.tight_layout()
plt.show()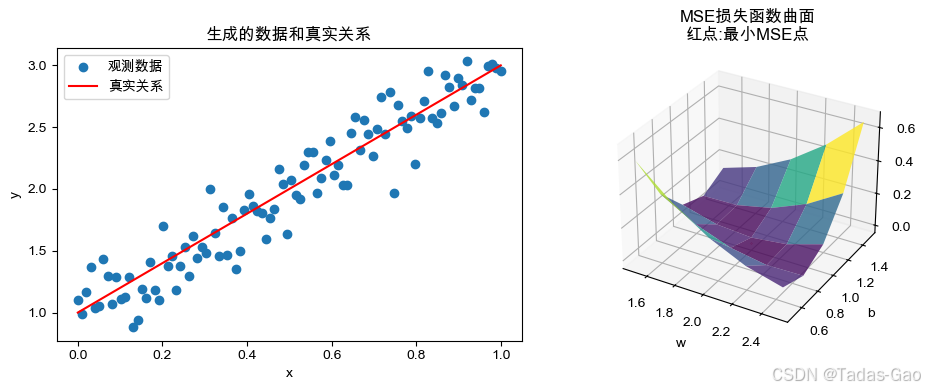

结论

通过上述推导，我们清晰地看到：

在线性回归中使用均方误差作为损失函数，源于对噪声项的高斯分布假设和最大似然估计原理。最小化平方误差等价于在高斯噪声假设下最大化数据的对数似然。

这一结论展示了机器学习中的一个重要原则：模型的选择和损失函数的设计不应是任意的，而应基于对数据和问题本质的概率理解（扩展阅读：线性模型选择中容易被忽视的关键洞察-优快云博客）。线性回归中平方误差的广泛使用，正是这种理论严谨性的完美体现（扩展阅读：线性回归性能评估：如何通过残差分析诊断模型问题-优快云博客）。

在机器学习领域，没有什么是凭空而来的。