线性回归是数据分析中最常用的建模技术之一,但许多分析师常常忽略对模型假设的验证,导致预测结果不可靠。本文将深入探讨如何通过残差分析来评估线性回归模型的性能,并识别可能存在的问题。
为什么残差分析至关重要
在统计学中,线性回归模型建立在几个关键假设之上,其中最重要的是关于误差项(残差)的假设:
-
残差应服从均值为0的正态分布
-
残差应具有同方差性(方差恒定)
-
残差之间应相互独立(无自相关)
残差分析是验证这些假设是否成立的最有效方法之一。当这些假设被违反时,模型的统计推断(如p值和置信区间)将变得不可靠,预测精度也会下降。
解读残差分布图
残差分布图是将模型预测值与实际观测值之间的差异(即残差)可视化呈现的工具。一个理想的残差分布图应具备以下特征:
良好的残差图特征
-
近似正态分布:残差应大致对称分布在零线周围
-
无明显模式:残差应随机分散,不呈现任何系统性的趋势或模式
-
恒定方差:残差的波动幅度在整个预测值范围内应保持一致
问题残差图的警示信号
-
偏斜分布:残差分布不对称,可能表明模型遗漏了重要变量或函数形式错误
-
异方差性:残差波动幅度随预测值变化,常见于金融、医疗等领域数据
-
模式结构:如U型或倒U型曲线,暗示模型可能遗漏了非线性关系
-
离群点聚集:可能表明数据中存在异常值或需要特殊处理的子群体
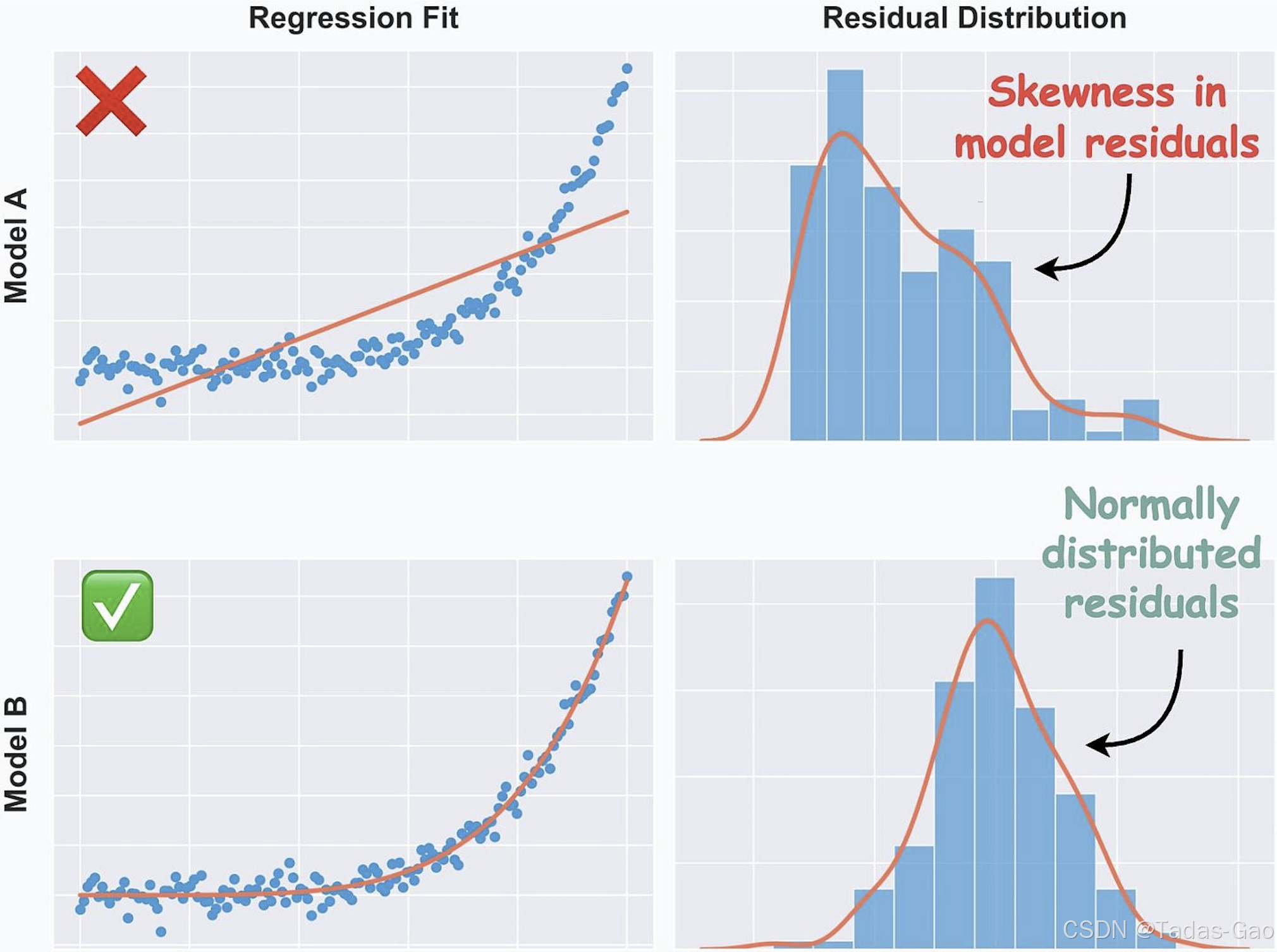
残差分析的实践价值
在高维数据场景下,直接可视化回归线变得困难甚至不可能。此时,残差分析的优势尤为明显:
-
降维可视化:无论原始数据维度多高,残差总是一维的,便于绘制和解释
-
诊断全面性:不仅能检测正态性假设,还能揭示异方差性、非线性等问题
-
问题定位:特定模式的残差图往往对应特定的模型缺陷,有助于针对性改进
超越残差分析:完整的模型诊断
虽然残差分析是模型诊断的核心工具,但完整的线性回归评估还应包括:
-
Q-Q图:更精确地检验残差正态性假设
-
杠杆值分析:识别对模型影响过大的观测点
-
方差膨胀因子(VIF):检测多重共线性问题
-
部分回归图:评估单个预测变量与响应变量的关系
-
Cook距离:衡量每个观测点对回归系数的影响程度
常见问题及解决方案
当残差分析发现问题时,可考虑以下改进措施:
| 问题类型 | 可能原因 | 解决方案 |
|---|---|---|
| 残差非正态 | 响应变量本身非正态分布 | 尝试变量变换(如对数变换)或使用广义线性模型 |
| 异方差性 | 误差方差与预测值相关 | 加权最小二乘法或稳健回归 |
| 非线性模式 | 遗漏重要变量或交互项 | 添加多项式项或考虑非线性模型 |
| 自相关 | 时间序列数据中的时间依赖 | 使用ARIMA模型或包含时间变量 |
实践建议
-
可视化先行:在进行任何统计检验前,先绘制残差图获取直观认识
-
多种工具并用:结合直方图、Q-Q图和散点图进行交叉验证
-
业务理解:将统计发现与领域知识结合,判断问题的实际意义
-
迭代改进:模型诊断是一个迭代过程,可能需要多次调整
代码示例
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
from statsmodels.stats.diagnostic import het_breuschpagan
from statsmodels.stats.outliers_influence import variance_inflation_factor
from scipy import stats
# 设置美观的绘图样式
sns.set_theme(style="whitegrid", palette="husl")
sns.set_theme(font='Arial Unicode MS') # 设置Seaborn字体
plt.rcParams['figure.facecolor'] = 'white' # 确保背景为白色
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
# 生成模拟数据 - 包含良好拟合和问题案例
np.random.seed(42)
# 案例1:良好拟合的线性回归
X_good = np.linspace(0, 10, 100)
y_good = 2 * X_good + np.random.normal(0, 1, 100)
# 案例2:异方差性问题
X_hetero = np.linspace(0, 10, 100)
y_hetero = 2 * X_hetero + np.random.normal(0, X_hetero, 100)
# 案例3:非线性关系问题
X_nonlinear = np.linspace(0, 10, 100)
y_nonlinear = 2 * X_nonlinear + 0.5 * X_nonlinear**2 + np.random.normal(0, 3, 100)
# 案例4:离群值问题
X_outlier = np.linspace(0, 10, 100)
y_outlier = 2 * X_outlier + np.random.normal(0, 1, 100)
y_outlier[95] += 15 # 添加一个极端离群值
# 将数据整理成DataFrame
def create_df(X, y, case_name):
df = pd.DataFrame({'X': X, 'y': y})
df['case'] = case_name
return df
df_good = create_df(X_good, y_good, "良好拟合")
df_hetero = create_df(X_hetero, y_hetero, "异方差性")
df_nonlinear = create_df(X_nonlinear, y_nonlinear, "非线性关系")
df_outlier = create_df(X_outlier, y_outlier, "离群值问题")
# 合并所有案例
all_data = pd.concat([df_good, df_hetero, df_nonlinear, df_outlier])
# 定义绘制残差分析图的函数
def plot_residual_analysis(df, title):
X = df['X'].values
y = df['y'].values
# 添加截距项并拟合模型
X_with_const = sm.add_constant(X)
model = sm.OLS(y, X_with_const).fit()
# 获取预测值和残差
predicted = model.predict(X_with_const)
residuals = y - predicted
# 创建图形
plt.figure(figsize=(15, 10))
plt.suptitle(f'残差分析: {title}', fontsize=16, y=1.02)
# 子图1: 原始数据与回归线
plt.subplot(2, 2, 1)
sns.scatterplot(x=X, y=y, color='blue', alpha=0.6)
plt.plot(X, predicted, color='red', linewidth=2)
plt.title('数据与回归线')
plt.xlabel('X')
plt.ylabel('y')
# 子图2: 残差与预测值
plt.subplot(2, 2, 2)
sns.scatterplot(x=predicted, y=residuals, color='green', alpha=0.6)
plt.axhline(y=0, color='red', linestyle='--')
plt.title('残差 vs 预测值')
plt.xlabel('预测值')
plt.ylabel('残差')
# 子图3: 残差直方图
plt.subplot(2, 2, 3)
sns.histplot(residuals, kde=True, color='purple')
plt.title('残差分布')
plt.xlabel('残差')
# 子图4: Q-Q图
plt.subplot(2, 2, 4)
stats.probplot(residuals, plot=plt)
plt.title('Q-Q图')
plt.tight_layout()
plt.show()
# 返回模型结果供进一步分析
return model
# 对每个案例进行分析
print("="*50)
print("案例1: 良好拟合的线性回归")
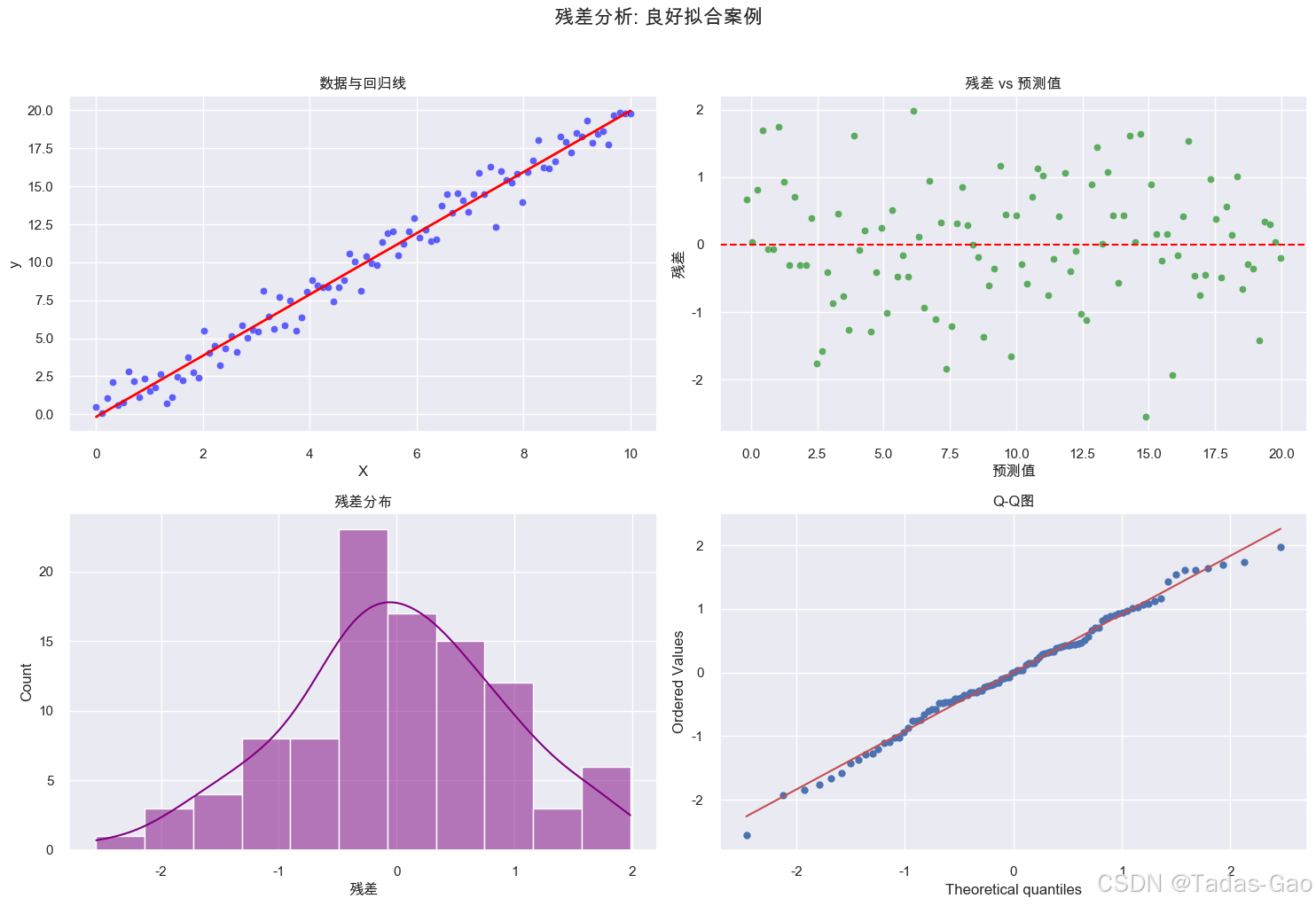
model_good = plot_residual_analysis(df_good, "良好拟合案例")
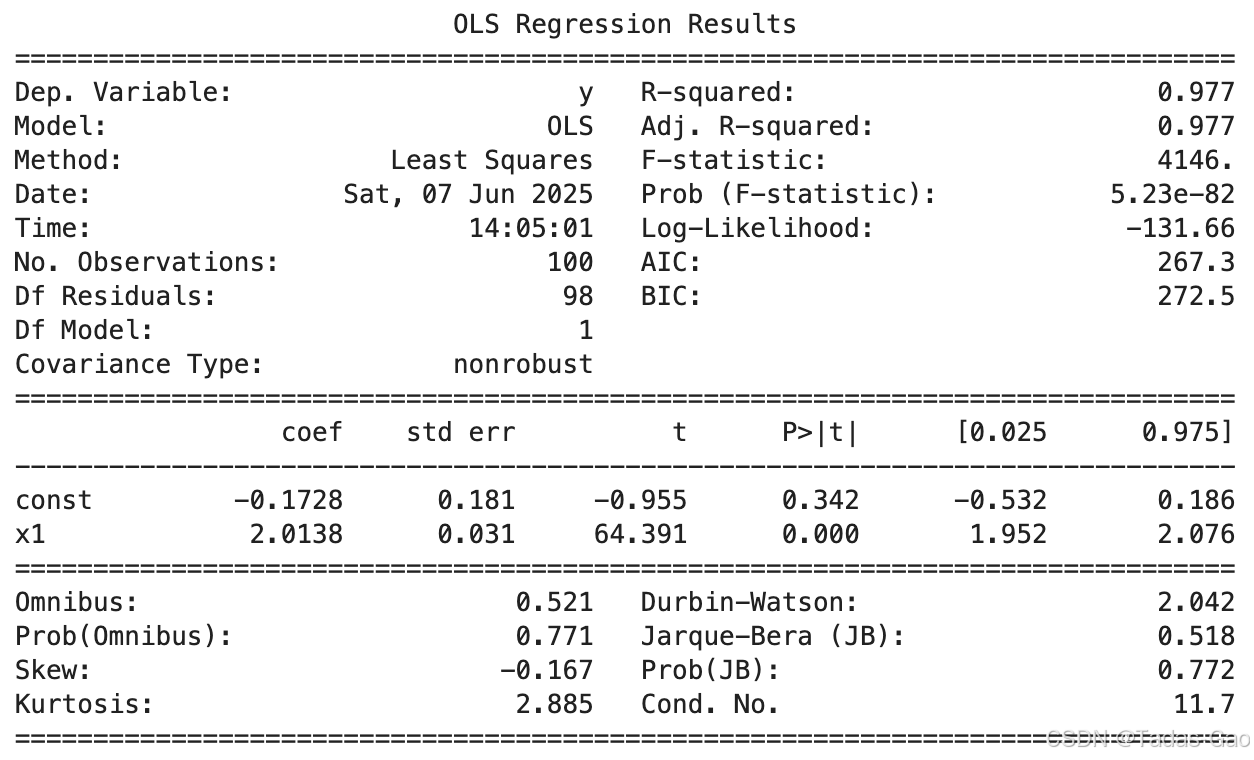
print(model_good.summary())
print("\n" + "="*50)
print("案例2: 异方差性问题")
model_hetero = plot_residual_analysis(df_hetero, "异方差性案例")
# 进行Breusch-Pagan检验
bp_test = het_breuschpagan(model_hetero.resid, model_hetero.model.exog)
print(f"\nBreusch-Pagan检验 (p值): {bp_test[1]:.4f}")
print("p值<0.05表明存在异方差性问题")
print("\n" + "="*50)
print("案例3: 非线性关系问题")
model_nonlinear = plot_residual_analysis(df_nonlinear, "非线性关系案例")
print("\n" + "="*50)
print("案例4: 离群值问题")
model_outlier = plot_residual_analysis(df_outlier, "离群值案例")
# 计算Cook距离
influence = model_outlier.get_influence()
cooks_d = influence.cooks_distance[0]
print(f"\n最大Cook距离: {np.max(cooks_d):.4f}")
print("Cook距离>1通常表示强影响点")
# 附加分析:方差膨胀因子(VIF)计算示例
print("\n" + "="*50)
print("附加分析: 多重共线性检查 (VIF)")
# 创建一个有多重共线性的示例数据集
from sklearn.datasets import make_regression
X_multi, y_multi = make_regression(n_samples=100, n_features=3, n_informative=2,
noise=10, random_state=42, coef=False)
# 人为制造共线性
X_multi[:, 2] = X_multi[:, 0] * 0.5 + X_multi[:, 1] * 0.5 + np.random.normal(0, 0.1, 100)
# 计算VIF
X_multi_df = pd.DataFrame(X_multi, columns=['X1', 'X2', 'X3'])
X_multi_with_const = sm.add_constant(X_multi_df)
vif_data = pd.DataFrame()
vif_data["feature"] = X_multi_with_const.columns
vif_data["VIF"] = [variance_inflation_factor(X_multi_with_const.values, i)
for i in range(X_multi_with_const.shape[1])]
print("\n方差膨胀因子(VIF):")
print(vif_data)
print("\nVIF>5表示可能存在共线性问题,VIF>10表示严重共线性")案例1:良好拟合的线性回归
案例2:异方差性问题
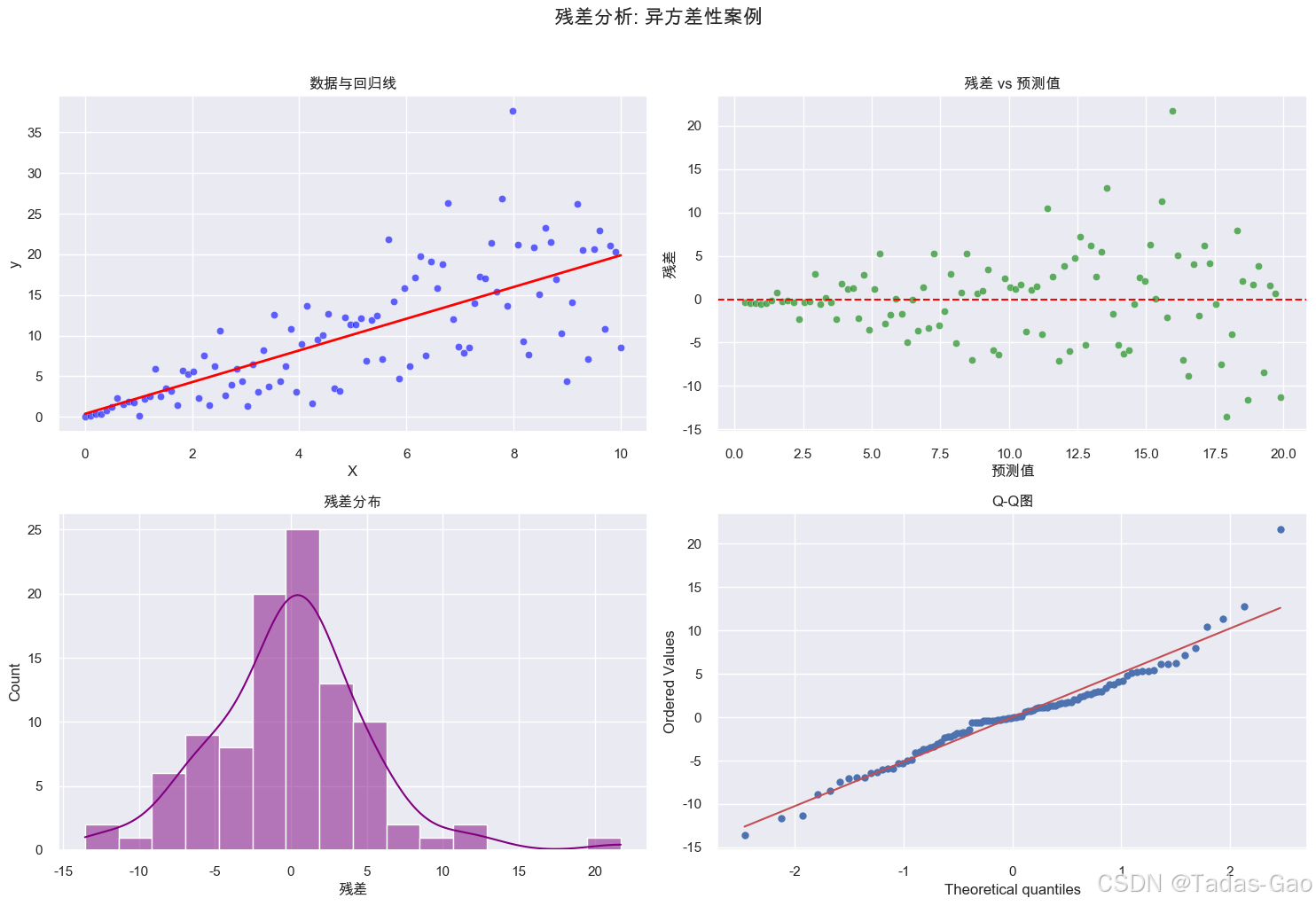
Breusch-Pagan检验 (p值): 0.0003
p值<0.05表明存在异方差性问题
案例3:非线性关系问题
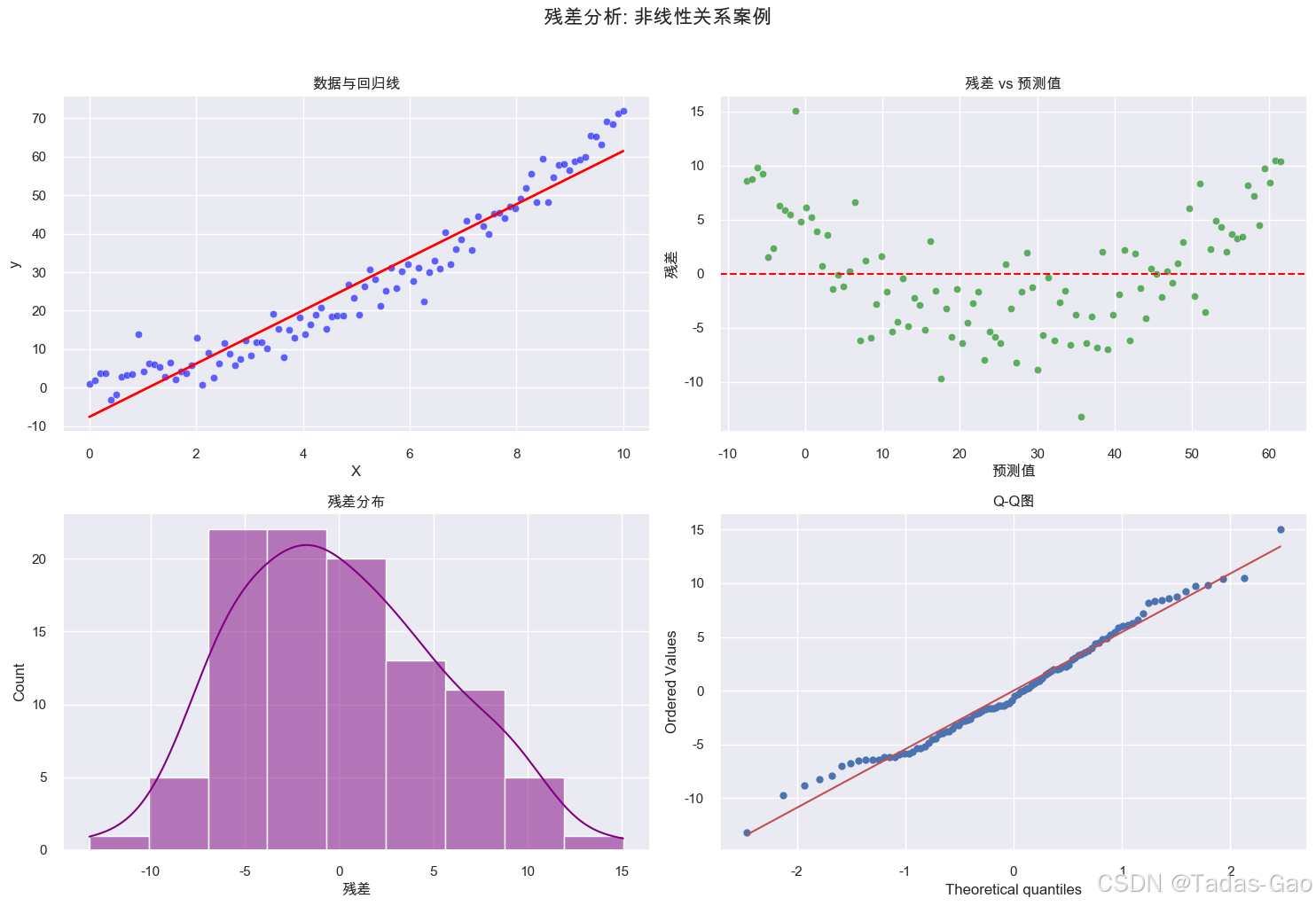
案例4:离群值问题
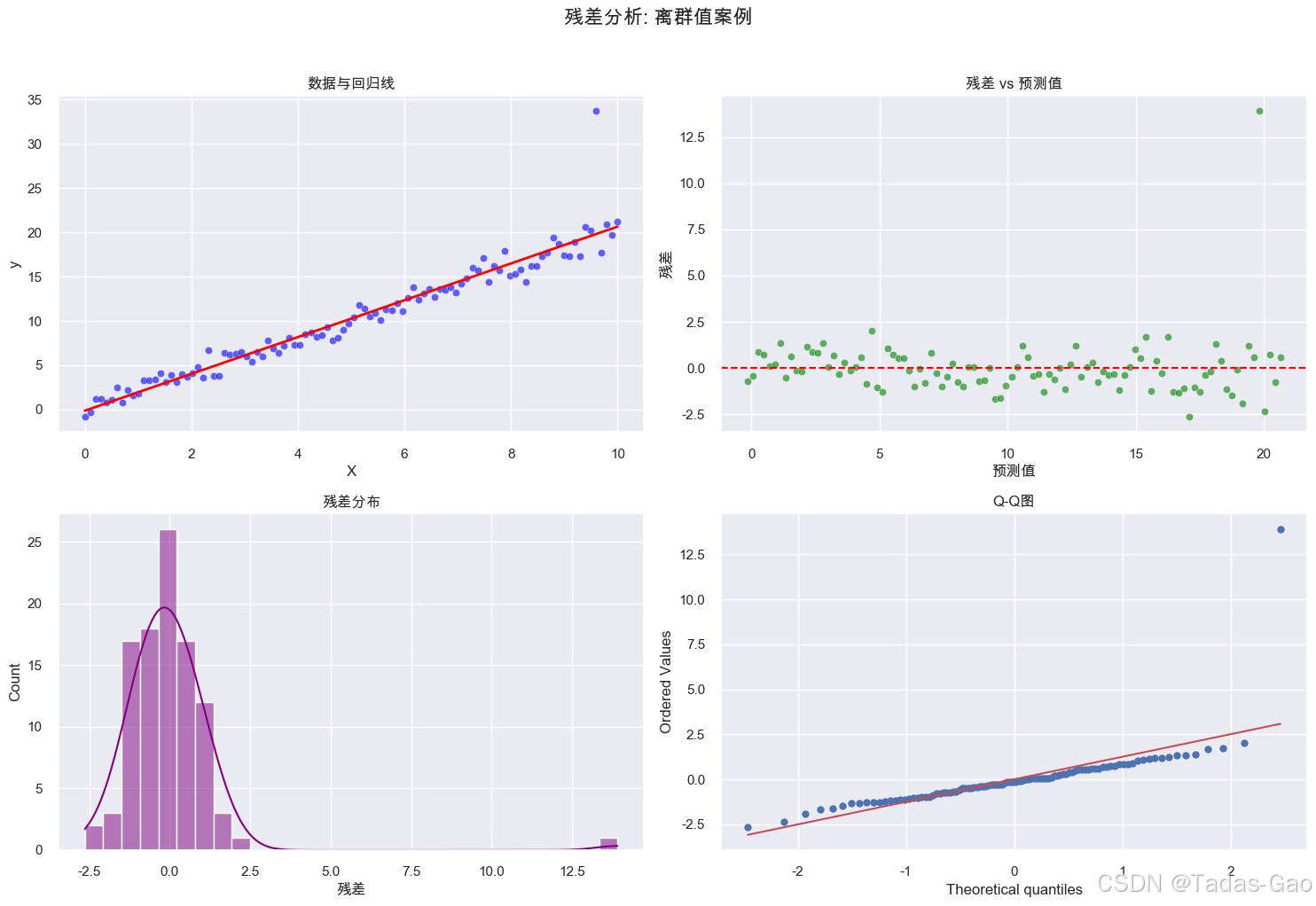
最大Cook距离: 1.2781
Cook距离>1通常表示强影响点
附加分析: 多重共线性检查 (VIF)
方差膨胀因子(VIF):
feature VIF
0 const 1.038653
1 X1 29.034360
2 X2 23.407031
3 X3 45.210300
VIF>5表示可能存在共线性问题,VIF>10表示严重共线性
总结
残差分析是线性回归模型诊断的基石,但往往被数据分析新手忽视。通过系统性的残差检查,我们不仅能验证模型假设,还能发现改进模型的机会。记住,一个好的模型不仅要有良好的预测能力,其残差也应"干净"地满足基本假设。掌握这些诊断技巧,将使你的回归分析结果更加可靠和有说服力。





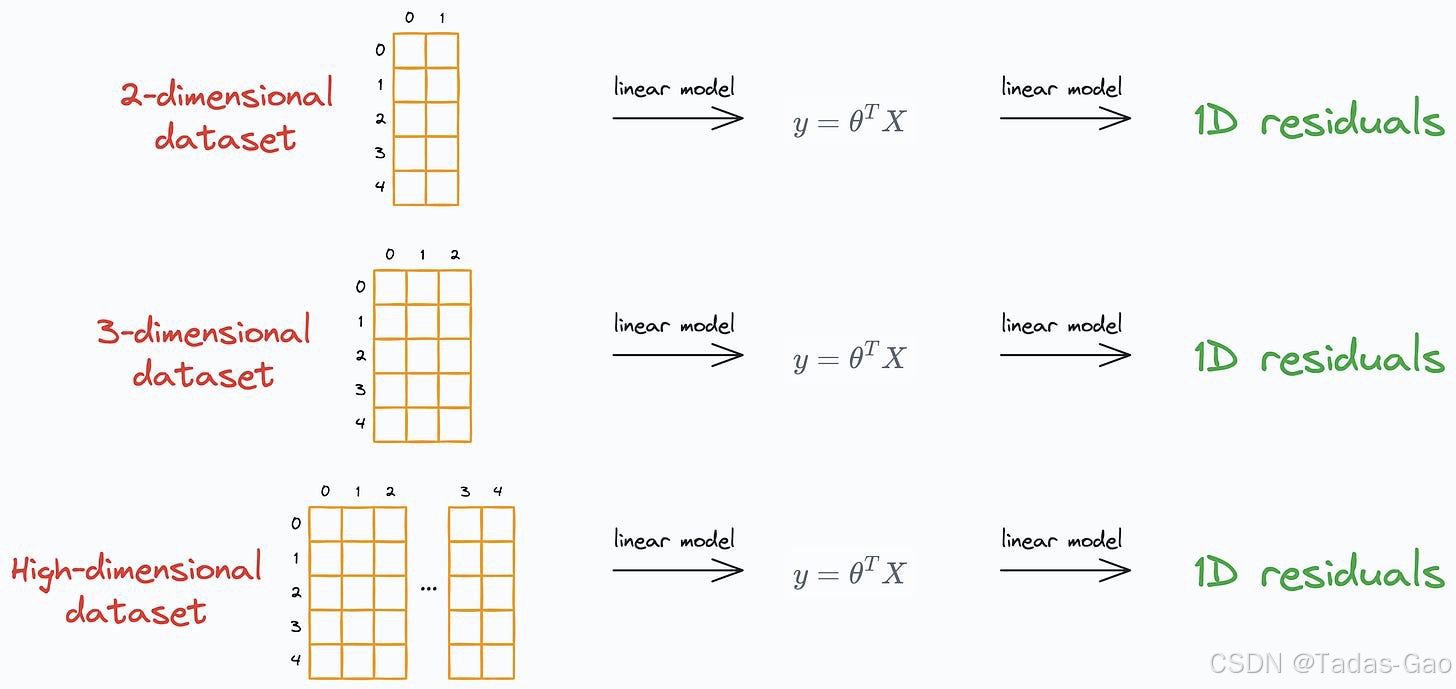



















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










