不会选损失函数？16种机器学习算法如何“扣分”？

在机器学习中，损失函数（Loss Function）就是算法“扣分”的方式——它决定了模型如何衡量预测值与真实值的差距，并指导模型如何调整参数以减少差距。不同的算法使用不同的损失函数，有的关注“误差平方”，有的关注“概率差距”，还有的压根不用损失函数（比如KNN）。

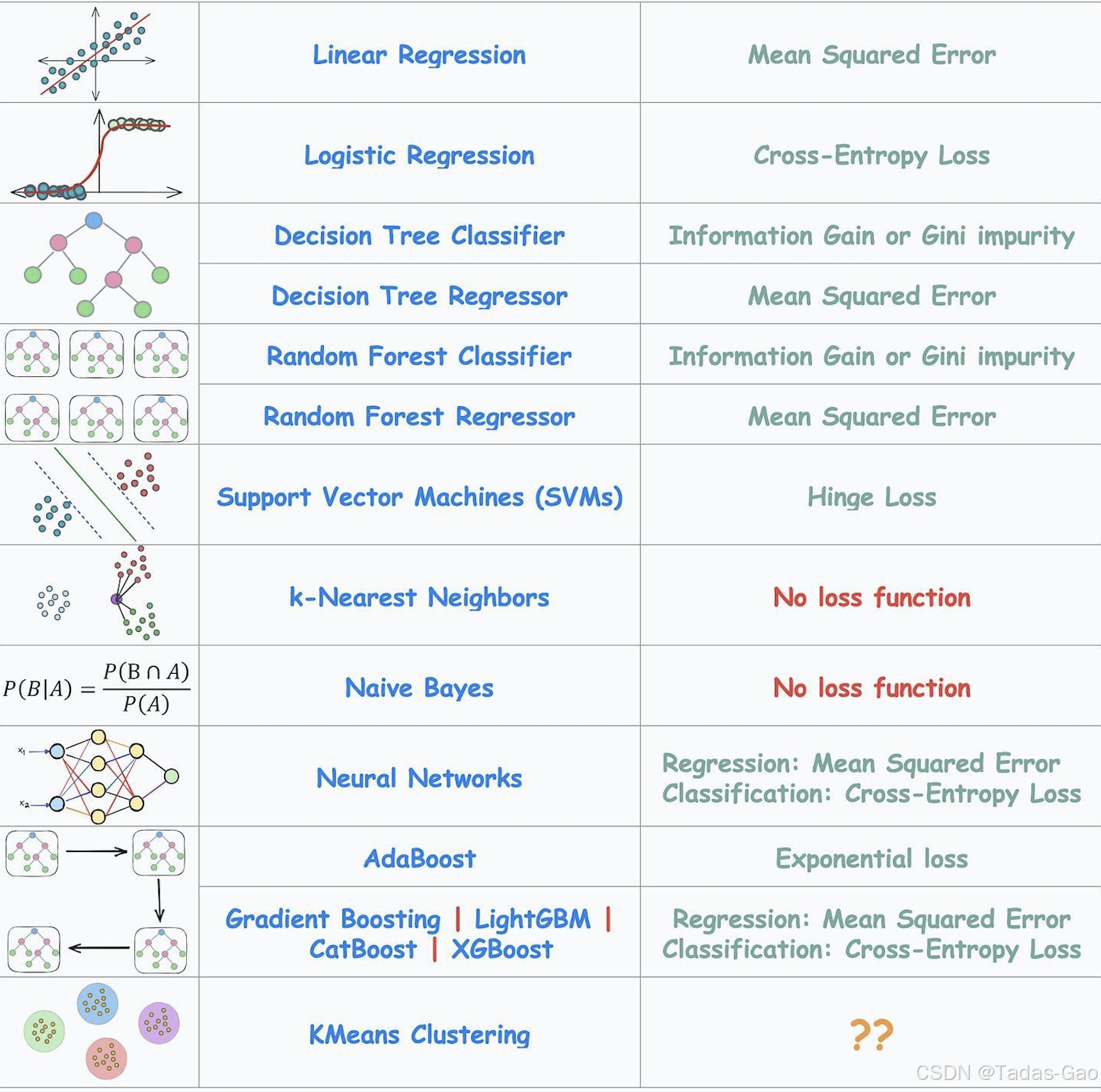
1. 线性回归（Linear Regression）→ 均方误差（MSE）

原理

MSE衡量预测值与真实值的平方误差均值，对异常值敏感但数学性质良好（可导、凸函数），适合线性回归的闭式解或梯度下降优化。

代码实现

from sklearn.metrics import mean_squared_error
y_true = [3, 5, 2.5, 7]
y_pred = [2.5, 5, 4, 8]
mse = mean_squared_error(y_true, y_pred)  # 输出：0.375

2. 逻辑回归（Logistic Regression）→ 交叉熵损失（Cross-Entropy Loss）

原理

通过最大化似然函数推导得出，适合二分类问题。对预测概率的错误惩罚呈对数增长，鼓励模型对正确分类的置信度提高。衡量预测概率分布与真实分布的差距，对错误预测惩罚更大（比如真实=1，但预测=0.01时损失极高）。

代码实现

from sklearn.metrics import log_loss
y_true = [1, 0, 1, 1]
y_pred_prob = [0.9, 0.1, 0.8, 0.7]
ce_loss = log_loss(y_true, y_pred_prob)
print("Cross-Entropy Loss:", ce_loss)

3. 决策树分类（Decision Tree Classifier）→ 基尼系数（Gini）或信息增益（Entropy）

原理

• 信息增益：基于信息熵，选择分裂后不确定性降低最多的特征。

• 基尼系数：计算随机抽两个样本类别不一致的概率，值越小纯度越高，计算更快且对类别分布敏感。

代码实现

from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier(criterion='gini')  # 或 criterion='entropy'
clf.fit(X_train, y_train)

4. 决策树回归（Decision Tree Regressor）→ 均方误差（MSE）

原理

分裂时选择使子节点MSE减少最多的特征，目标是最小化区域内的方差。

代码实现

from sklearn.tree import DecisionTreeRegressor
reg = DecisionTreeRegressor(criterion='mse') # 新版sklearn已改用'squared_error'
reg.fit(X_train, y_train)

5. 随机森林分类（Random Forest Classifier）→ 同决策树（Gini/Entropy）

原理

与单棵决策树相同，每棵树用基尼系数或信息增益，但通过集成多棵树降低过拟合。

代码实现

from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(n_estimators=100, criterion='gini')
clf.fit(X_train, y_train)

6. 随机森林回归（Random Forest Regressor）→ 均方误差（MSE）

原理

每棵树使用MSE，最终预测为所有树的平均值。

代码实现

from sklearn.ensemble import RandomForestRegressor
reg = RandomForestRegressor(n_estimators=100, criterion='mse')
reg.fit(X_train, y_train)

7. 支持向量机（SVM）→ 合页损失（Hinge Loss）

原理

对正确分类且置信度高的样本损失为0，否则线性增长（用于最大化分类间隔）。

代码实现

from sklearn.svm import LinearSVC
svm = LinearSVC(loss='hinge')  # 等价于SVC(kernel='linear')
svm.fit(X_train, y_train)

8. K近邻（KNN）→ 无损失函数

原理

• KNN：基于距离投票，无显式优化过程。

• 朴素贝叶斯：基于贝叶斯定理计算后验概率，无损失函数。

9. 神经网络回归（Neural Networks Regression）→ 均方误差（MSE）

原理

与线性回归类似，但通过反向传播优化非线性关系。

代码实现

import torch.nn as nn
loss_fn = nn.MSELoss()

10. 神经网络分类（Neural Networks Classification）→ 交叉熵损失（Cross-Entropy Loss）

原理

常结合Softmax输出层，优化多分类问题的概率分布。

代码实现

loss_fn = nn.CrossEntropyLoss()  # 已包含Softmax

11. AdaBoost → 指数损失（Exponential Loss）

原理

对误分类样本的权重指数级增加，强调难样本的纠正。

代码实现

from sklearn.ensemble import AdaBoostClassifier
clf = AdaBoostClassifier(algorithm='SAMME', n_estimators=50)
clf.fit(X_train, y_train)

12. Gradient Boosting系列 -> MSE (回归) / Cross-Entropy (分类)

原理

通过梯度下降逐步拟合残差（回归）或概率误差（分类）。

代码实现

import xgboost as xgb
# 回归
reg = xgb.XGBRegressor(objective='reg:squarederror')
# 分类
clf = xgb.XGBClassifier(objective='binary:logistic')

13. KMeans Clustering -> Sum of Squared Errors (SSE)

原理

最小化簇内样本到质心的平方距离之和，等价于MSE但无监督。

代码实现

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3)
kmeans.fit(X)
print("SSE:", kmeans.inertia_)

扩展阅读

10 个最常用的损失函数-优快云博客