开始之前,可以先回顾一下:初探注意力机制-优快云博客
简单的例子,来理解一下 Q、K、V。
-
Q(Query):比如“今晚吃啥?”
-
K(Key):菜单上的菜名(关键词),比如“红烧肉”“青菜”。
-
V(Value):菜的实际内容(具体信息),比如“红烧肉=肥而不腻”。
注意力机制就是:用你的问题(Q)去匹配菜单(K),找到最相关的菜,然后返回它的描述(V)。
注意力机制的分数计算公式,如下:
Softmax 将任意实数向量转换为概率分布:
为避免指数溢出,实际实现中会减去最大值:
举个简单的例子。
假设我们有⼀个句⼦:“The teacher said”,词向量如下:
假设,主要用于缩放,避免注意力分数过大,直接计算 softmax 后,导致赢者通吃的现象。
假设 Q、K、V 的权重矩阵都是 3 * 3 的矩阵,矩阵如下:
计算 Q
计算各自的 Q,如下:
计算 K
计算各自的 K,如下:
计算 V
计算各自的 V,如下:
以上计算得到了三个词的 Q、K、V,共 9 个向量,每个词的这三个新的向量是自注意力层的基础。
计算注意力得分
接下来计算注意力得分。对于任意一个词,它的 Q 向量会和其他所有词的 K 向量做点积运算,得到一系列的注意力 得分。得分越大,表示该词与对应的其他词相关性越强;得分越小,表示二者关系较弱。也可以认为这个得分代表了这个词对其他词的重要性。
计算 The 与所有词的注意力得分:
计算 teacher 与所有词的注意力得分:
计算 said 与所有词的注意力得分:
接下来计算缩放后的得分:
计算 The 与所有词的缩放得分:
计算 teacher 与所有词的缩放得分:
计算 said 与所有词的缩放得分:
数值稳定性处理(减去最大值),调整后的结果:
计算 The 与所有词的缩放得分:
计算 teacher 与所有词的缩放得分:
计算 said 与所有词的缩放得分:
接下来对得分进行 softmax 计算,目的是为了转化成总和为 1 的概率分布,并不会改变得分的意义。
计算 The 的三个注意力得分转化:
计算 teacher 的三个注意力得分转化:
计算 said 的三个注意力得分转化:
最后,用上一步得到的注意力权重与 V 向量进行加权求和,得到新的向量表示。
计算 The 的输出:
计算 teacher 的输出:
计算 said 的输出:
最终每个词都会生成新的向量表示(上下文表示),这些表示会进一步传递到后续网络层或解码器。
结合图,再来理解一下。
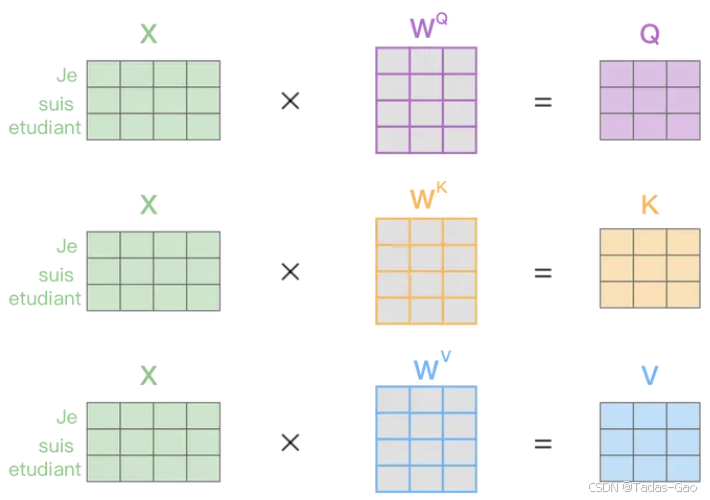
得到Q、K、V之后就可以计算出Self-Attention的输出,如下图所示:
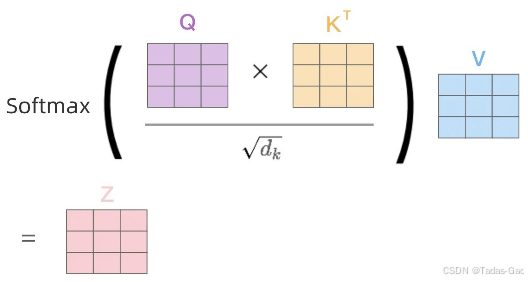























 443
443

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










