Basic Structure：Set

Preamble：本文只是记录个人认为本章的重难点，选择忽视了很多基础内容

Defination and Equality

集合是否相同与元素的个数和顺序无关

Notation

universal set

全集并不等于全部，而是相对意义上的全部

Subset 子集的充要条件

A = {1,2} and B = {{1,2}} A ⊆ B is false.B contains one set, not the elements 1 and 2

Identity 恒等式

举一个例子，因为A∪B以后会多出很多元素是两集合共同拥有的子集

Cardinality 基数

集合的基数是指集合中不同元素的数量the cardinality of A, written |A| (and also cardA or #A)

注意和元素中的元素数量加以区分（包含相同元素）

Power set 幂集(我觉得翻译的不好)

是集合的基本运算之一。由集合的所有子集构成的集合。

symmetric difference 对称差

 Difference 差集

Complement 补集

Cartesian products 集合的笛卡尔积

笛卡尔积(向量积）  Cartesian product 或 叉集  product set 

、

Counting and enumeration 计数和枚举       

counting string 

因为每一个位置都有2种可能，将所有位置的可能相乘

从二进制字符推广，每个位置有m种可能，一共有n个位置

Describe setsA in relation with setsB

translation： P(A)的每个元素（即 A 的每个子集）都会产生长度为 n=|A 的二进制数串。
 反过来说，每一个长度为 n 的二进制字符串都可以被用来以唯一的方式构造一个 A 的子集。
 反之，每条长度为 n 的二进制弦都可以被用来以唯一的方式构造 A 的子集。
 二进制字符串和子集之间的这种对应关系就是投射。
 因此，|P(A)| 正是长度等于 2n 的二进制字符串的数目。

Arrangement(permutation) & Combination 排列组合

translation： 假设我们要组成一个长度为 n 的字符串，其中第一个符号来自一个有 k1 个元素的字母表 A1，第二个符号来自一个有 k2 个元素的字母表 A2。
 字母表 A1，其中有 k1 个元素；第二个符号来自字母表 A2，其中有
 k2 个元素，依此类推，直到第 n 个符号来自具有 kn
 元素的字母表 An。
 长度为 n 的字符串可能有多少个？

 设 m∈N 为任意值，并假设 a,b∈N 满足 a⊥b。那么
 (a | m) 和 (b | m)，当且仅当 ab | m。
 因此，问一个自然数 m 是否能被 a 和 b 整除，等同于问它是否能被 ab 整除。
 就等于问它是否能被 ab 整除。但只有当 a⊥b 时才成立。
 我们注意到，一般来说，问一个自然数 m 是否能被 a 和 b 整除与问它是否能被 ab 整除是一样的。
 就等于问它是否能被 a 和 b 的最小公倍数整除。

Binomial Expansion 二项式系数，展开

 

如此表示组合是方便计算机运算和表示

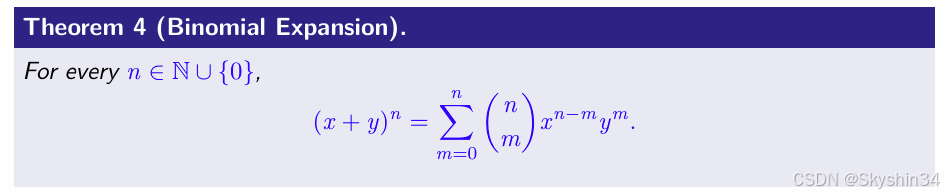
如果二项式种有常数则常数作为B

我们看到幂级数从未停止，但现在存在收敛问题因为我们增加的项数是无限的（与几何级数相比）。 可以证明，幂级数在 |x| < 1 时收敛（与几何级数的条件相同）。 与几何级数的条件相同）

应用：

---

Reference：

【集合论】集合恒等式 ( 幂等律 | 交换律 | 结合律 | 分配率 | 德摩根律 | 吸收率 | 零律 | 同一律 | 排中律 | 矛盾律 | 余补律 | 双重否定定律 | 补交转换律 )-优快云博客

【离散数学】集合论 第三章 集合与关系(5) 集合的笛卡尔积、笛卡尔积对交/并的分配律、集合计数的乘法原理_笛卡尔积证明交和并分配律-优快云博客