二阶系统固有频率、频带宽度和响应的含义及其之间的关系

固有频率

固有频率是指一个初始稳定的系统（一般指系统的输出及其各阶导为0），在没有阻尼的情况下，受到外界一个激励信号，系统就会产生无衰减的周期振荡，这个振荡的频率就被称为系统的固有频率。

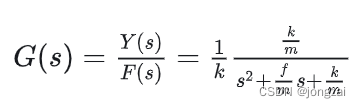
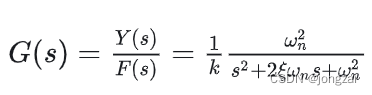
频带宽度

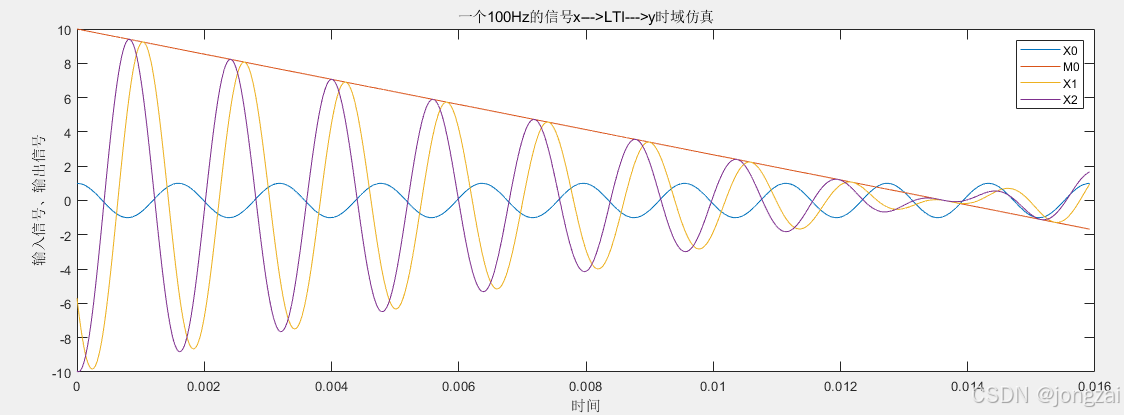
ω=100Hz的信号经过LTI系统(时域仿真)

f0=100;%该信号的频率为100Hz
T0=1/f0;%该信号的周期为0.01s
Fs0=5000;%该信号1个周期的采样点数
N1=1;
t0=0:T0/(N1*Fs0-1):T0;%相应的1个周期的时间序列
fff=(0:N1*Fs0-1)*(Fs0/(N1*Fs0));%采样频率范围内的频率序列，步长是1.
X0=1*cos(2*pi*f0*t0);%1个周期的该信号序列
plot(t0,X0)
hold on
M0=(-0.10*t0+11);
plot(t0,M0)
X1=1*M0.*cos(2*pi*f0*t0-268/2/pi);%1个周期的该信号序列
plot(t0,X1)
X2=1*M0.*cos(2*pi*f0*t0-286/2/pi);%1个周期的该信号序列
plot(t0,X2)


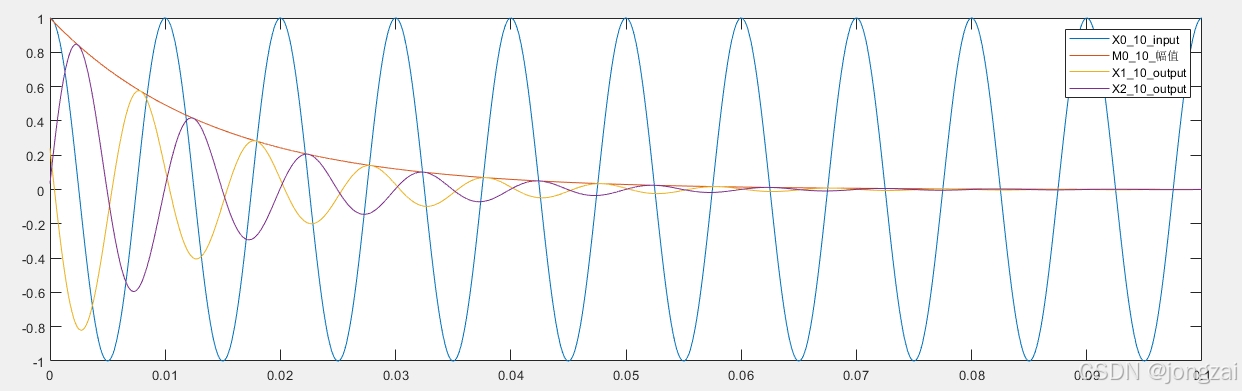
N10=10;%该信号的10个周期
t0_10=0:N10*T0/(N10*Fs0-1):N10*T0;%相应的10个周期的时间序列
fff_10=(0+10:N10*Fs0-1+10)*(Fs0/(N10*Fs0));%采样频率范围内的频率序列，步长是十分之一。
X0_10=1*cos(2*pi*f0*t0_10);%10个周期的该信号序列
plot(t0_10,X0_10)
hold on
%M0_10=(-1100/1.5*t0_10+10);%线性衰减模拟
M0_10=exp(-0.707*99.97*t0_10);%指数衰减模拟
plot(t0_10,M0_10)
X1_10=1*M0_10.*cos(2*pi*f0*t0_10-268/2/pi);%10个周期的该信号序列
plot(t0_10,X1_10)
X2_10=1*M0_10.*cos(2*pi*f0*t0_10-286/2/pi);%10个周期的该信号序列
plot(t0_10,X2_10)

ω=100Hz的信号经过LTI系统(频域分析)

X0_fft=fft(X0);
X1_fft=fft(X1);
X2_fft=fft(X2);
G01=X1_fft./X0_fft;
G_frd=frd(G01, fff, 'frequencyunit', 'hz');
G02=X2_fft./X0_fft;
G_frd02=frd(G02, fff, 'frequencyunit', 'hz');
semilogx(fff,20*log(abs(X1_fft)./abs(X0_fft)))
semilogx(fff,180*(angle(X1_fft)-angle(X0_fft))/pi-360)
hold on
semilogx(fff,180*(angle(X2_fft)-angle(X0_fft))/pi-360)

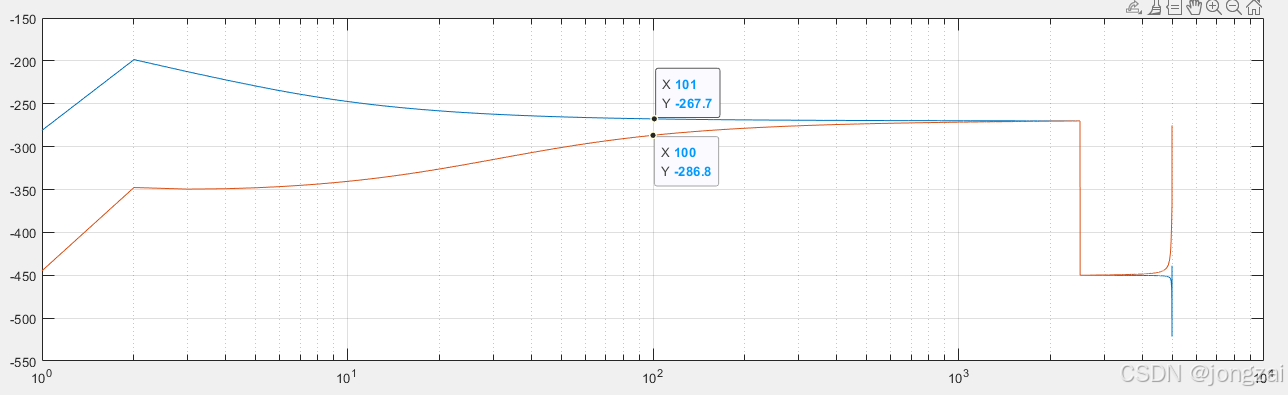
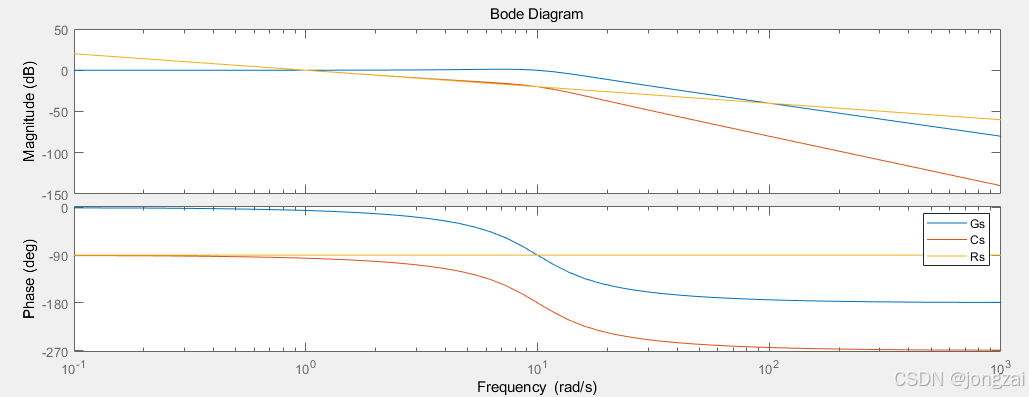
ω=sqrt(75)/2/piHz的二阶LTI系统举例(频域分析)

s=tf('s');
G=1/(1+0.02*s+0.001*s^2);
wn=10;
wd=sqrt(75);
zeta=0.5;
Gs=wn^2/((s+zeta*wn)^2+wd^2);%二阶系统
bode(Gs)
Rs=1/s;%阶跃输入
Cs=Gs*Rs;%阶跃响应
bode(Cs)

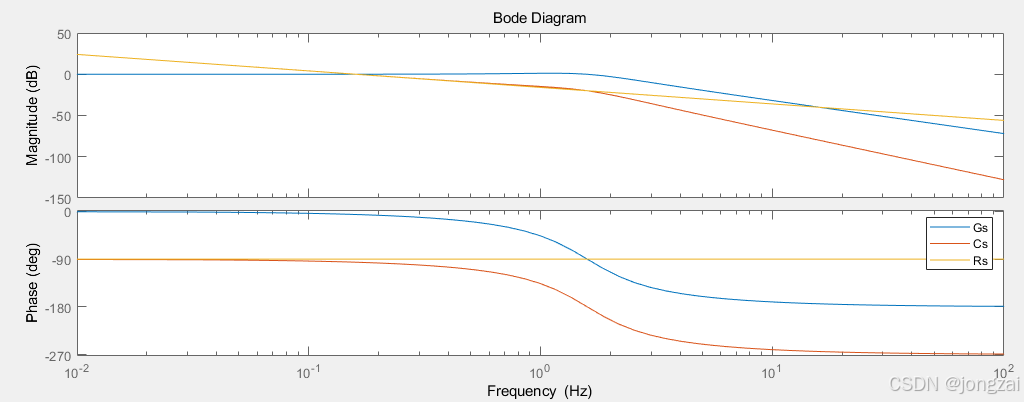
ω=sqrt(75)/2/piHz的二阶LTI系统阶跃响应(时域仿真)

f0=sqrt(75)/2/pi;%1/该信号的频率为xHz
T0=1/f0;%该信号的周期为xs
Fs0=5000;%该信号1个周期的采样点数
N1=1;
t0=0:T0/(N1*Fs0-1):T0;%相应的1个周期的时间序列
fff=(0:N1*Fs0-1)*(Fs0/(N1*Fs0));%采样频率范围内的频率序列，步长是1.
X0=1*sin(2*pi*f0*t0);%1个周期的该信号序列
plot(t0,X0)
hold on
zeta=0.5;
wn=2*pi*f0/sqrt(1-zeta*zeta);
M0=exp(-zeta*wn*t0)/sqrt(1-zeta*zeta);
plot(t0,M0)
M1=1+exp(-zeta*wn*t0)/sqrt(1-zeta*zeta);
plot(t0,M1)
C0=1-exp(-zeta*wn*t0).*cos(2*pi*f0*t0)-1*zeta*M0.*sin(2*pi*f0*t0);%1个周期的该信号序列
% C0=1*wn*M0.*sin(2*pi*f0*t0);%1个周期的该信号序列
plot(t0,C0)
C1=1-exp(-zeta*wn*t0).*cos(2*pi*f0*t0-268/2/pi)-1*zeta*M0.*sin(2*pi*f0*t0-268/2/pi);%1个周期的该信号序列
plot(t0,C1)
C2=1-exp(-zeta*wn*t0).*cos(2*pi*f0*t0-286/2/pi)-1*zeta*M0.*sin(2*pi*f0*t0-286/2/pi);%1个周期的该信号序列
plot(t0,C2)

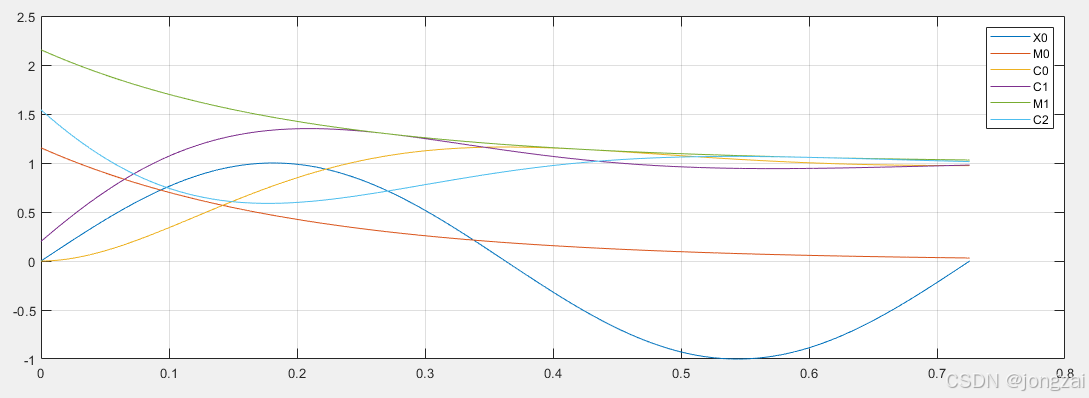
N10=10;%该信号的10个周期
t0_10=0:N10*T0/(N10*Fs0-1):N10*T0;%相应的10个周期的时间序列
fff_10=(0+10:N10*Fs0-1+10)*(Fs0/(N10*Fs0));%采样频率范围内的频率序列，步长是十分之一。
X0_10=1*cos(2*pi*f0*t0_10);%10个周期的该信号序列
plot(t0_10,X0_10)
hold on
M0_10=exp(-zeta*wn*t0_10)/sqrt(1-zeta*zeta);
plot(t0_10,M0_10)
M1_10=1+exp(-zeta*wn*t0_10)/sqrt(1-zeta*zeta);
plot(t0_10,M1_10)
C0_10=1-exp(-zeta*wn*t0_10).*cos(2*pi*f0*t0_10)-1*zeta*M0_10.*sin(2*pi*f0*t0_10);%10个周期的该信号序列
% C0_10=1*wn*M0_10.*sin(2*pi*f0*t0_10);%10个周期的该信号序列
plot(t0_10,C0_10)
C1_10=1-exp(-zeta*wn*t0_10).*cos(2*pi*f0*t0_10)-1*zeta*M0_10.*sin(2*pi*f0*t0_10-268/2/pi);%10个周期的该信号序列
plot(t0_10,C1_10)
C2_10=1-exp(-zeta*wn*t0_10).*cos(2*pi*f0*t0_10)-1*zeta*M0_10.*sin(2*pi*f0*t0_10-286/2/pi);%1个周期的该信号序列
plot(t0_10,C2_10)

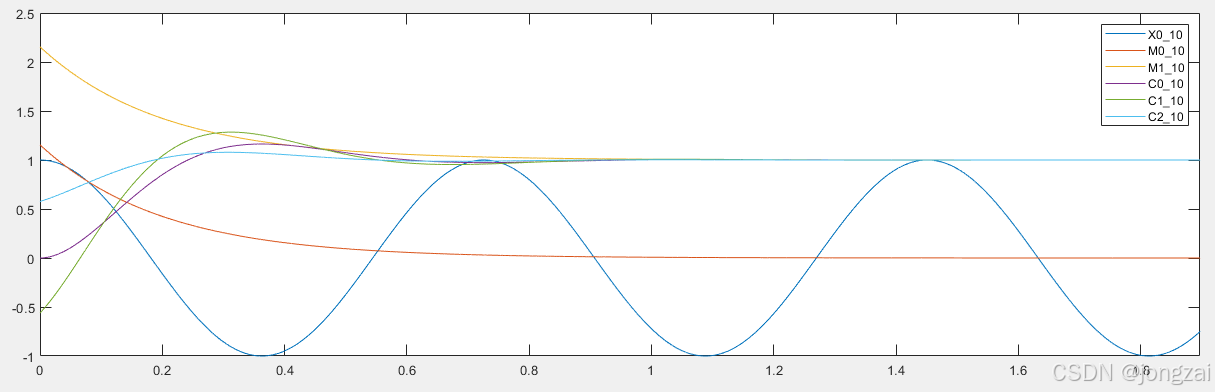
阶跃信号经过二阶LTI系统后的输出(频域计算)

fff=(0:N1*Fs0-1)*(f0/(N1*Fs0));%采样频率范围内的频率序列，步长是1.
C0_fft=fft(C0);
semilogx(fff,20*log(abs(C0_fft)/sqrt(5000)))
semilogx(fff,180*(angle(C0_fft))/pi-360)
C0_frd=frd(C0_fft, fff, 'frequencyunit', 'hz');
bode(C0_frd)

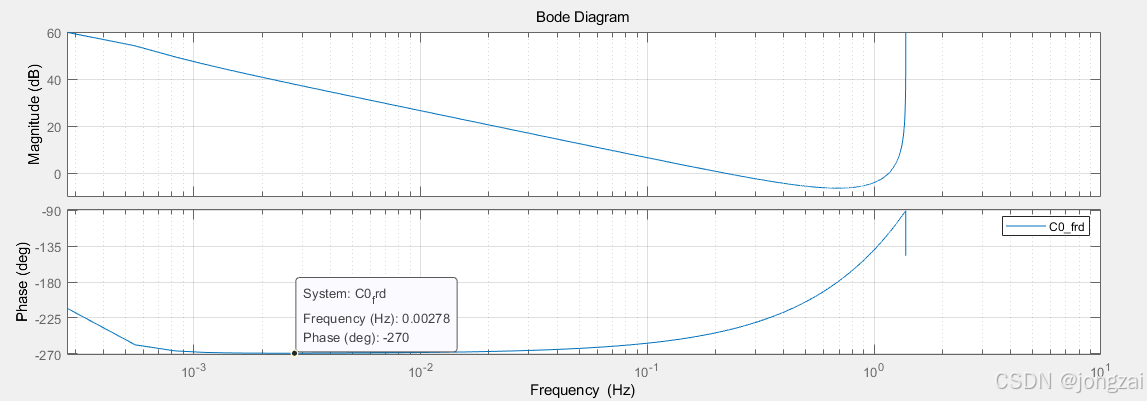
ω=sqrt(75)/2/piHz的正弦信号经过二阶LTI系统后的输出(频域响应分析)

固有频率和频带宽度与系统的响应有什么关系呢？

在这里插入图片描述