【计算机组成原理】2、二进制原码反码补码、左移右移、进制转换，进制相减、内存地址偏移计算与容量计算

一、二进制的原码、反码、补码

1、二进制最高位是符号位：0表示正数，1表示负数
2、正数的原码、反码、补码都是一样
3、负数的反码=原码符号位不变，其它位取反(0->1,1->0)
4、负数的补码=反码+1
5、0的反码、补码都是0
6、在计算机运算的时候都是以补码的方式来运算
7、原码是给人用的（比如想知道53的原码，则因为 53 = 32 + 16 + 4 + 1, 且53为正数, 所以53的原码为0011 0101，然后可推算出53的反码、53的补码）

1.1 二进制计算

2 & -3
        原码            反码        补码
2   =>  0000 0010   0000 0010   0000 0010
-3  =>  1000 0011   1111 1100   1111 1101
------------------------------------------------
                                0000 0000

                                反推原码也为0 (因为0的原码、反码、补码均为0)

2 | -3
        原码            反码        补码
2   =>  0000 0010   0000 0010   0000 0010
-3  =>  1000 0011   1111 1100   1111 1101
------------------------------------------------
                                1111 1111
                                
                                反推为原码：(因为补码运算结果首位为1所以补码为负数, 所以得到补码，再得到原码)
         原码       补码         运算结果
         1000 0001  1111 1110   1111 1111
         结果为： -1

2 ^ -2
        原码            反码        补码
2   =>  0000 0010   0000 0010   0000 0010
-2  =>  1000 0010   1111 1101   1111 1110
------------------------------------------------
                                1111 1100
                        
                                反推为原码：(因为补码运算结果首位为1所以补码为负数, 所以得到补码，再得到原码)
        反码         补码        运算结果
        1000 0100   1111 1011   1111 1100
        结果为： -4

2 ^ 4
        原码            反码        补码
2   =>  0000 0010   0000 0010   0000 0010
4   =>  0000 0100   0000 0100	0000 0100
------------------------------------------------
                                0000 0110
                        
                                反推为原码：(因为补码运算结果首位为0所以补码为正数, 而正数的原码、反码、补码均相同)
        反码         补码        运算结果
        0000 0110   0000 0110   0000 0110
        结果为： 6

func main() {
	a, b := 2, -3
	fmt.Printf("%4d原码: %08b\n", a, a)
	fmt.Printf("%4d原码: %08b\n", b, b)
	fmt.Printf("%4d原码: %08b\n", a&b, a&b)
	fmt.Printf("%4d原码: %08b\n", a|b, a|b)
	fmt.Printf("%4d原码: %08b\n", a^(-a), a^(-a))
	fmt.Printf("%4d原码: %08b\n", a^(2*a), a^(2*a))
}
   2原码: 00000010
  -3原码: -0000011
   0原码: 00000000
  -1原码: -0000001
  -4原码: -0000100
   6原码: 00000110

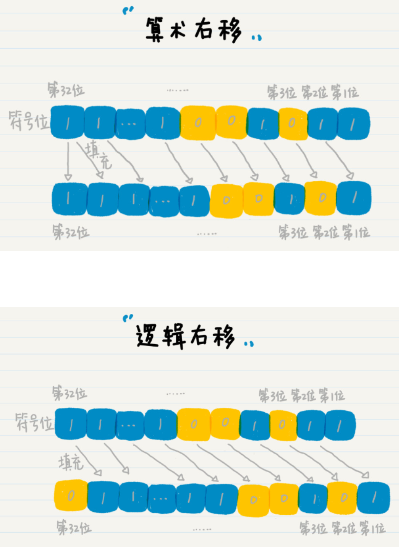
1.2 左移、右移

二进制左移一位，就是乘以2
二进制右移一位，就是除以2

• 类型：
  • 算数右移（>>）：移动所有位，同时保留原符号位
  • 逻辑右移（>>>）：移动所有位，同时固定新符号位为 0
• 编程语言：
  • Java、Python：>> 为算数右移，>>> 为逻辑右移
  • C、C++、go：只有 >>，若 signed 则算数右移，若 unsigned 则算数右移和逻辑右移等价

func main() {
	var a uint8 = 53
	fmt.Printf("%4d原码: %08b\n", a, a) 			//  53原码: 00110101
	fmt.Printf("%4d原码: %08b\n", a>>1, a>>1)		//  26原码: 00011010
	fmt.Printf("%4d原码: %08b\n", a>>2, a>>2)		//  13原码: 00001101
}
因为 53 = 32 + 16 + 4 + 1, 且53为正数, 所以53的原码为0011 0101
         原码            反码        补码
53   =>  0011 0101	 0011 0101   0011 0101
// 由53的补码 右移一位 得到26的补码, 进而算出26的反码, 进而算出26的补码
26   =>  0001 1010   0001 1010	 0001 1010 
// 由26的补码 右移一位 得到13的补码, 进而算出13的反码, 进而算出13的补码
13   =>  0000 1101   0000 1101	 0000 1101 



func main() {
	var a uint8 = -53
	fmt.Printf("%4d原码: %08b\n", a, a) 			//  -53原码: -0110101
	fmt.Printf("%4d原码: %08b\n", a>>1, a>>1)		//  -27原码: -0011011
	fmt.Printf("%4d原码: %08b\n", a>>2, a>>2)		//  -14原码: -0001110
}
因为 53 = 32 + 16 + 4 + 1, 且-53为负数, 所以-53的原码为1011 0101
而负数的反码=原码符号位不变，其它位取反(0->1,1->0), 所以-53的反码为1100 1010
而负数的补码=反码+1, 所以-53的补码为1100 1011
          原码            反码        补码
-53   =>  1011 0101	  1100 1010   1100 1011
// 由-53的补码 右移一位 得到-27的补码, 进而算出-27的反码, 进而算出-27的补码
-27   =>  						  1110 0101
// 由-27的补码 右移一位 得到-14的补码, 进而算出-14的反码, 进而算出-14的补码
-14   =>  						  1111 0010



func main() {
	var a int = 128
	fmt.Printf("%4d原码: %08b\n", a, a)       // 128原码: 10000000
	fmt.Printf("%4d原码: %08b\n", a>>1, a>>1) //  64原码: 01000000
	fmt.Printf("%4d原码: %08b\n", a>>2, a>>2) //  32原码: 00100000
}
因为 128 = 128 + 0, 且 128 为正数, 所以128的原码为1000 0000
而正数的原码、反码、补码均相同，所以得到其反码、补码如下：
          原码            反码        补码
128   =>  1000 0000	  1000 0000   1000 0000
// 由128的补码，右移一位，得到补码0100 0000, 因为0100 0000为正数, 所以其反码和补码均为此数，换算为十进制的64
64    =>  0100 0000	  0100 0000   0100 0000
// 由64的补码，右移一位，得到补码0010 0000, 因为0010 0000为正数, 所以其反码和补码均为此数，换算为十进制的32
32    =>  0010 0000	  0010 0000   0010 0000



func main() {
	var a int8 = -128
	fmt.Printf("%4d原码: %08b\n", a, a)				// -128原码: -10000000
	fmt.Printf("%4d原码: %08b\n", a>>1, a>>1)		//  -64原码: -1000000
	fmt.Printf("%4d原码: %08b\n", a>>2, a>>2)		//  -32原码: -0100000
}
因为 128 = 128 + 0, 且 -128 为负数, 所以-128的原码为1000 0000
而负数的反码=原码符号位不变，其它位取反(0->1,1->0), 所以-128的反码为0111 1111
而负数的补码=反码+1, 所以-128的补码为1000 0000
           原码            反码        补码
-128   =>  1000 0000	  0111 1111   1000 0000
// 由-128的补码，右移一位，得到补码1100 0000, 因为1100 0000为负数, 所以其反码为1011 1111, 所以其原码为1100 0000，换算为十进制的-64(即-1 * 64)
-64    =>  1100 0000	  1011 1111   1100 0000
// 由-64的补码， 右移一位，得到补码1110 0000, 因为1110 0000为负数, 所以其反码为1101 1111, 所以其原码为1010 0000，换算为十进制的-64(即-1 * 32)
-32    =>  1010 0000	  1101 1111   1110 0000

1.3 异或

“异或”操作的本质其实就是，所有数值和自身进行按位的“异或”操作之后都为 0。而且要通过“异或”操作得到 0，也必须通过两个相同的数值进行按位“异或”。这表明了两个数值按位“异或”结果为 0，是这两个数值相等的必要充分条件，可以作为判断两个变量是否相等的条件。

110100 ^ 100011 = 010110

二、进制转换

对于整数，有四种表示方式：
1)、二进制：0,1 ，满 2 进 1。在 golang 中，不能直接使用二进制来表示一个整数，它沿用了 c 的特点。
2)、十进制：0-9 ，满 10 进 1。
3)、八进制：0-7 ，满 8 进 1. 以数字 0 开头表示。
4)、十六进制：0-9 及 A-F，满 16 进 1. 以 0x 或 0X 开头表示。此处的 A-F 不区分大小写

简单的格式化进制输出的示例
package main
import "fmt"
func main() {
	var i int = 5; fmt.Printf("%b\n", i)   // 十进制格式化为二进制
	var j int = 011; fmt.Println("j=", j)  // 八进制格式化为十进制
	var k int = 0x11; fmt.Println("k=", k) // 十六进制格式化为十进制
}

2.1 二进制、八进制、十六进制转为十进制

// 二进制转为十进制
例如：1011
手动换算：1 * 2^(4-1) + 0 * 2^(3-1) + 1 * 2^(2-1) + 1 * 2^(1-1)
              8     +      0      +      2      +   1    =   11    
代码运算：
	ret, _ := strconv.ParseInt("1011", 2, 64) // 11


// 八进制转为十进制
例如：23
手动换算：2 * 8^(2-1) + 3 * 8^(1-1)
              16     +      3     =     19        
代码运算：
	ret, _ := strconv.ParseInt("23", 8, 64) // 19


// 十六进制转为十进制
例如：23
手动换算：2 * 16^(2-1) + 3 * 16^(1-1)
              32     +      3     =     35  
代码运算：
	ret, _ := strconv.ParseInt("23", 16, 64) // 35

2.2 十进制转为二进制、八进制、十六进制

// 十进制转为二进制
例如：56
手动换算：         余数，从下往上取值
	2 | 56   ...   0
	2 | 28   ...   0
	2 | 14   ...   0
	2 | 7    ...   1
	2 | 3    ...   1
	  1      ...   1
    111000
代码运算：
	ret := strconv.FormatInt(56, 2) // 111000


// 十进制转为八进制
例如：56
手动换算：         余数，从下往上取值
	8 | 56  ...  0
	  7     ...  7  //小于8，从下往上取值
    70
代码运算：
	ret := strconv.FormatInt(56, 8) // 70


// 十进制转为十六进制
例如：56
手动换算：         余数，从下往上取值
	16 | 56  ...   8
	   3     ...   3  //小于16，从下往上取值
    38
代码运算：
	ret := strconv.FormatInt(56, 16) // 38

2.3 二进制转为八进制、十进制、十六进制

// 二进制转为八进制
例如： 11010101
手动换算：每取3位，进行 4 2 1 按位的运算
    421=3  421=2   421=5
	011    010     101
	结果：0325
代码运算：
	// 2进制转为10进制
	base_10, _ := strconv.ParseInt("11010101", 2, 64) //213

	// 10进制转为8进制
	ret := fmt.Sprintf("%o", base_10) //325
	fmt.Println(ret)



// 二进制转为十六进制
因 $2^4=16$，所以每4个二进制位，可表示为1个十六进制。例如如下：
- 00001111(B) = F(H)、0xF、0x0F
- 11111111(B) = FF(H)、0xFF
- 111100001111(B) = F0F(H)、0xF0F
- 1111111100001111(B) = FF0F(H)、0xFF0F

例如： 11010101
手动换算：每取4位，进行 8 4 2 1 按位的运算
        8421=13   8421=5
		1101      0101
		D5
代码运算：
	// 2进制转为10进制
	base_10, _ := strconv.ParseInt("11010101", 2, 64) //213

	// 10进制转为16进制
	ret := fmt.Sprintf("%X", base_10) //D5
	fmt.Println(ret)



// 二进制转为十进制
例如： 11010101
手动换算：
		// 先转为16进制
		每取4位，进行 8 4 2 1 按位的运算
        8421=13   8421=5
		1101      0101
		D5
		// 然后再由十六进制转为10进制
		D * (16^2-1) + 5 * (16^1-1) 
        13*16        + 5    =   213
代码运算：
	// 2进制转为10进制
	base_10, _ := strconv.ParseInt("11010101", 2, 64) //213

2.4 八进制、十进制、十六进制转为二进制

// 八进制为二进制
例如： 123
手动换算：采用：421，按位换算
	421    421   421 
	001    010   011
	  1     2      3
-----------------------
	123 ==> 001010011
代码运算：
	// 8进制转为2进制
	ret := fmt.Sprintf("%b", 0123)
	fmt.Println(ret) //1010011



// 十进制为二进制
例如： 123
手动换算：取2，取余数，从下往上取值
	2 | 123 ... 1
    2 |  61 ... 1
    2 |  30 ... 0
    2 |  15 ... 1
    2 |   7 ... 1
    2 |   3 ... 1
	2 |   1 ... 1
---------------------
    1111011
代码运算：
	// 10进制转为2进制
	ret := fmt.Sprintf("%b", 123) // 1111011
	fmt.Println(ret) 



// 十六进制为二进制
每1个十六进制 转换为 4个二进制位即可。例如如下：
- 0xF0F = 111100001111(B) = 0000111100001111(B)
- 0xFF0F = 1111111100001111(B)

例如： 123
手动换算：取4位，采用：8421，按位换算
	8421    8421   8421 
	0001    0010   0011
	1       2      3
-----------------------
	123 ==> 000100100011
代码运算：
	// 16进制转为2进制
	ret := fmt.Sprintf("%b", 0x123)
	fmt.Println(ret) //100100011

三、进制相减

3.1 十六进制

例如：0xA000 - 0x0800

• 先从末尾开始减：最后两位的0x0000-0x0000 = 0x0000
• 再倒数第三位相减 0x0000 - 0x0800，因为不够减，所以借位得到16（因为是十六进制相减），即 16 - 8 = 8
• 在倒数第四位相减 0xA000 - 0x0000，因为已经被借走了一位，则变为 0x9000 - 0x0000 = 0x9000
  故最终答案为 0x9800

PS：类比二进制相减即容易理解了

四、内存地址偏移计算

例如：若一栋楼共100层，最底为第0层，则最顶为第99层。因为从0到(n-1)共有n个数，如下图：

4.1 根据首末地址，求存储容量

题目 如下：

如下图所示，首地址是 30000H，末地址是 AFFFFH。

因为题目说明内存以字节编制，则说明即每个地址是一个字节（即楼房的每层放了1个byte，即8个bit）。

题意问存储容量，即问能存储多少 bit。

---

题解如下：

• 先求楼层数：

  • AFFFF(H) - 30000(H) + 1 = 7FFFF(H) + 1 = 80000(H)
  • 而 80000(H) = 1000-0000-0000-0000-0000(B) = 2^19，即 2 ^ 19 Bytes
    
  • 而 $2^{1}0=1K$、$2^{2}0=1M$、$2^{3}0=1G$
  • 故 2 ^ 19 bytes = $2^9$ * $2^{10}$ = $2^{9}Kbytes$ = $2^{9}KB$ = 512 KB
    

• 故最终答案为能存储 512 KB 的容量（如下图）：

4.2 根据末地址 和 存储容量，求首地址

题目如下：

---

题解如下：

若题目未指明，则默认每个地址为 1个字节。

因为共 2KB 即 2K Bytes 即 2048 Bytes，需将 2000（十进制）转换为 十六进制。

因常识为 1024 = $2^{10}$，故 2000 = $2^{11}$ = 2后面1个0(B) = 1000-0000-0000(B) = 800(H) 即 0x800。详见下图：

而因公式为 $存储空间=末地址-首地址+1$，故 $首地址=末地址-存储空间+1$ = 9FFF(H) - 0800(H) + 1(B)= A000(H) - 0800(H) = 9800(H)。详见下图：