玩转数据结构(03)--栈

栈（Stack）

栈是一种线性数据结构；具有不可思议的作用

相比数组，栈对应的操作是数组的子集

栈只能从一端添加元素，也只能从同一端取出元素，这一端称为栈顶

图解：向栈中添加元素【入栈】（4只能在3的上面，只能从一端添加元素）

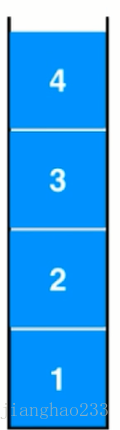
从栈中取出栈顶元素【出栈】（只能先取出 4,用户甚至都看不到其他的值）

由此可知：数组是一种后进先出的数据结构(Last In First Out)[LIFO]

栈的应用：

1.无处不在的 Undo (撤销)操作 

例：文档中依次输入 沉迷  学习  不法  ---实际上是将这些元素压入栈中

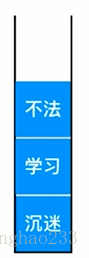
执行 Undo 操作，--实际是从栈中拿出栈顶元素，通过栈顶元素来确认最近一次的操作是什么；

然后将其删除，成功删除（出栈）后

2. 程序调用的系统栈 

例：子过程（子逻辑）的调用在编译器内部的实现机理

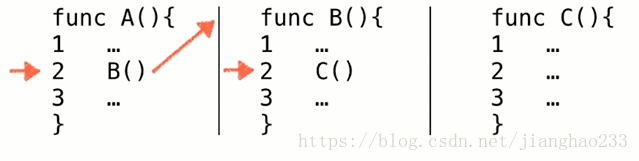
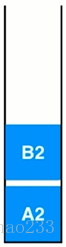
A2: 程序执行到了A函数的第二行，发生中断去执行函数B

B2：程序执行到了B函数的第二行，发生中断去执行函数C

当都执行完成后，接下来如何执行需要看系统栈了，对当前的栈来说，栈顶元素是B2；故跳到B2处继续执行，然后B2出栈，

接着执行B3完成整个函数B；接下来如何执行需要再看系统栈了，栈顶元素是A2，故跳到A2处继续执行，然后A2出栈，接着执行A3完成整个函数A；接下来如何执行需要再看系统栈，栈中已经没有元素了，表示没有之前中断的程序了，故系统知道已经没有要执行的程序了。

二、栈的实现

栈的基本操作：

Stack<E>

void push(E)   --- 【入栈】向栈中添加元素              时间复杂度：O(1)

E pop()   ---【出栈】从栈中拿出栈顶元素                 时间复杂度：O(1)

E peek()   ---查看栈顶元素                                        时间复杂度：O(1)

int getSize()  ---查看栈中总共有多少个元素              时间复杂度：O(1)

boolean isEmpty()   ---判断栈是否为空                     时间复杂度：O(1)

实现基于动态数组的栈：

示例代码:Array.java(复用上章数组的代码)

public class Array<E> {

    private E[] data;
    private int size;

    // 构造函数，传入数组的容量capacity构造Array
    public Array(int capacity){
        data = (E[])new Object[capacity];
        size = 0;
    }

    // 无参数的构造函数，默认数组的容量capacity=10
    public Array(){
        this(10);
    }

    // 获取数组的容量
    public int getCapacity(){
        return data.length;
    }

    // 获取数组中的元素个数
    public int getSize(){
        return size;
    }

    // 返回数组是否为空
    public boolean isEmpty(){
        return size == 0;
    }

    // 在index索引的位置插入一个新元素e
    public void add(int index, E e){

        if(index < 0 || index > size)
            throw new IllegalArgumentException("Add failed. Require index >= 0 and index <= size.");

        if(size == data.length)
            resize(2 * data.length);

        for(int i = size - 1; i >= index ; i --)
            data[i + 1] = data[i];

        data[index] = e;

        size ++;
    }

    // 向所有元素后添加一个新元素
    public void addLast(E e){
        add(size, e);
    }

    // 在所有元素前添加一个新元素
    public void addFirst(E e){
        add(0, e);
    }

    // 获取index索引位置的元素
    public E get(int index){
        if(index < 0 || index >= size)
            throw new IllegalArgumentException("Get failed. Index is illegal.");
        return data[index];
    }

    public E getLast(){			//(新增代码)取出最后一个元素
        return get(size - 1);
    }

    public E getFirst(){		//(新增代码)取出第一个元素
        return get(0);
    }

    // 修改index索引位置的元素为e
    public void set(int index, E e){
        if(index < 0 || index >= size)
            throw new IllegalArgumentException("Set failed. Index is illegal.");
        data[index] = e;
    }

    // 查找数组中是否有元素e
    public boolean contains(E e){
        for(int i = 0 ; i < size ; i ++){
            if(data[i].equals(e))
                return true;
        }
        return false;
    }

    // 查找数组中元素e所在的索引，如果不存在元素e，则返回-1
    public int find(E e){
        for(int i = 0 ; i < size ; i ++){
            if(data[i].equals(e))
                return i;
        }
        return -1;
    }

    // 从数组中删除index位置的元素, 返回删除的元素
    public E remove(int index){
        if(index < 0 || index >= size)
            throw new IllegalArgumentException("Remove failed. Index is illegal.");

        E ret = data[index];
        for(int i = index + 1 ; i < size ; i ++)
            data[i - 1] = data[i];
        size --;
        data[size] = null; // loitering objects != memory leak

        if(size == data.length / 4 && data.length / 2 != 0)
            resize(data.length / 2);
        return ret;
    }

    // 从数组中删除第一个元素, 返回删除的元素
    public E removeFirst(){
        return remove(0);
    }

    // 从数组中删除最后一个元素, 返回删除的元素
    public E removeLast(){
        return remove(size - 1);
    }

    // 从数组中删除元素e
    public void removeElement(E e){
        int index = find(e);
        if(index != -1)
            remove(index);
    }

    @Override
    public String toString(){

        StringBuilder res = new StringBuilder();
        res.append(String.format("Array: size = %d , capacity = %d\n", size, data.length));
        res.append('[');
        for(int i = 0 ; i < size ; i ++){
            res.append(data[i]);
            if(i != size - 1)
                res.append(", ");
        }
        res.append(']');
        return res.toString();
    }

    // 将数组空间的容量变成newCapacity大小
    private void resize(int newCapacity){

        E[] newData = (E[])new Object[newCapacity];
        for(int i = 0 ; i < size ; i ++)
            newData[i] = data[i];
        data = newData;
    }
}

Stack.java

public interface Stack<E> {

    int getSize();		//查看栈中总共有多少个元素
    boolean isEmpty();	//判断栈是否为空
    void push(E e);		//【入栈】向栈中添加元素
    E pop();			//【出栈】从栈中拿出栈顶元素
    E peek();			//查看栈顶元素
}

ArrayStack.java

public class ArrayStack<E> implements Stack<E> {

    private Array<E> array;

    public ArrayStack(int capacity){	//参数：数组容量capacity
        array = new Array<>(capacity);
    }

    public ArrayStack(){
        array = new Array<>();
    }

    @Override
    public int getSize(){
        return array.getSize();
    }

    @Override
    public boolean isEmpty(){
        return array.isEmpty();
    }

    public int getCapacity(){		//查看静态数组的容量
        return array.getCapacity();
    }

    @Override
    public void push(E e){
        array.addLast(e);
    }

    @Override
    public E pop(){
        return array.removeLast();
    }

    @Override
    public E peek(){
        return array.getLast();
    }

    @Override
    public String toString(){		//便于打印输出
        StringBuilder res = new StringBuilder();
        res.append("Stack: ");
        res.append('[');
        for(int i = 0 ; i < array.getSize() ; i ++){
            res.append(array.get(i));
            if(i != array.getSize() - 1)
                res.append(", ");
        }
        res.append("] top");	//栈顶在数组右侧
        return res.toString();
    }
}

Main.java

public class Main {

    public static void main(String[] args) {

        ArrayStack<Integer> stack = new ArrayStack<>();

        for(int i = 0 ; i < 5 ; i ++){	//入栈测试（依次）
            stack.push(i);
            System.out.println(stack);
        }

        stack.pop();		//出栈测试
        System.out.println(stack);
    }
}

输出：

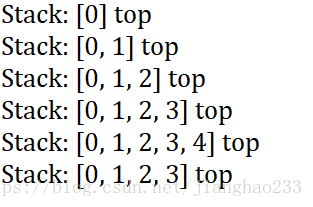
三、栈的另一个应用--（括号匹配）

题目描述：

思路分析：声明一个栈，然后逐一遍历字符串中的每一个字符，如果这个字符是一个左括号，就将其压入栈中；完成之后，判断右括号是否和栈顶的左括号相匹配，如果匹配成功就可以出栈；直至所有的都匹配成功，这时所有的元素都出栈，栈为空时表明字符串是一个有效的字符串。如果不是有效的字符串，在右括号与左括号相匹配时不能匹配成功，直接停止返回这是一个错误的字符串。

栈顶元素反映了在嵌套的层次关系中，最近的需要匹配的元素

示例代码：Solution.java

import java.util.Stack;

class Solution {

    public boolean isValid(String s) {

        Stack<Character> stack = new Stack<>();		//声明栈stack
        for(int i = 0 ; i < s.length() ; i ++){
            char c = s.charAt(i);		//获取字符串的第i个元素
            if(c == '(' || c == '[' || c == '{')	//将左括号压入栈中
                stack.push(c);
            else{
                if(stack.isEmpty())
                    return false;

                char topChar = stack.pop();	//拿出栈顶元素
                if(c == ')' && topChar != '(')
                    return false;
                if(c == ']' && topChar != '[')
                    return false;
                if(c == '}' && topChar != '{')
                    return false;
            }
        }
        return stack.isEmpty();	//判断栈是否为空
    }

    public static void main(String[] args) {

        System.out.println((new Solution()).isValid("()[]{}"));    //传入测试用例
        System.out.println((new Solution()).isValid("([)]"));
    }
}

输出：