本文探讨了动态数组的概念，解决数组空间不足的问题。详细分析了动态数组的添加、删除、修改和查找操作的时间复杂度，并介绍了均摊复杂度的概念以解决复杂度震荡问题。此外，还给出了resize操作在不同情况下的时间复杂度考虑。
在上篇博客基础上继续--《玩转数据结构(01)--数组》
1.动态数组（解决数组空间不够用的情况）
Java 中的静态数组，当插入的值数量 > 数组的size 时就会报错，使用动态数组可以解决这个问题，
设置动态数组的思路：再建立一个新的数组newData，它要比之前的数组空间大一些；将data 中的数据放入到 newData 中，循环遍历数组data中所有的元素，将他们依次赋值到 newData 中；
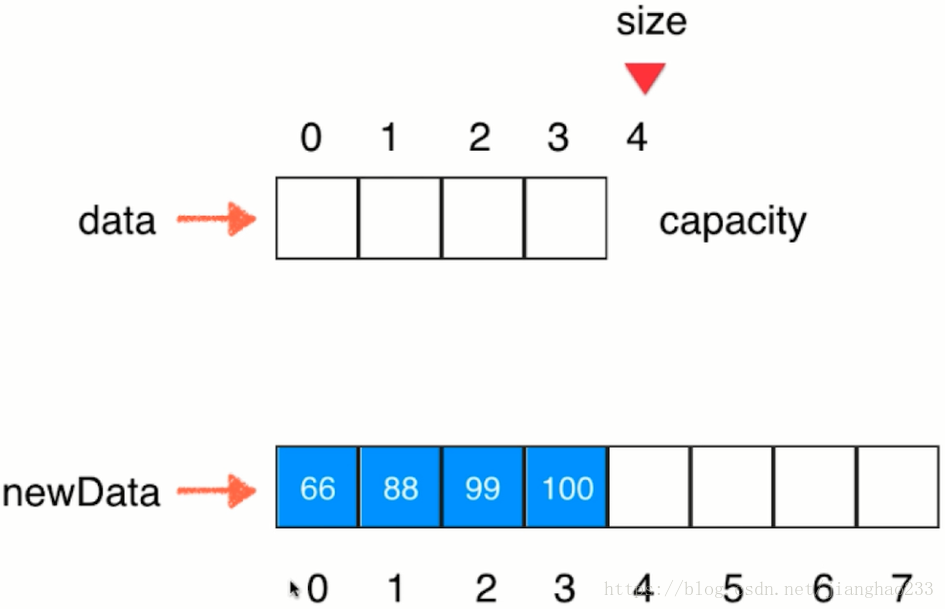
想让 newData 取代原来的 data ,对数组而言，容量（capacity）已经变为 8 ；size 在newData中还是 4 ，但数组可以装入更多的元素；
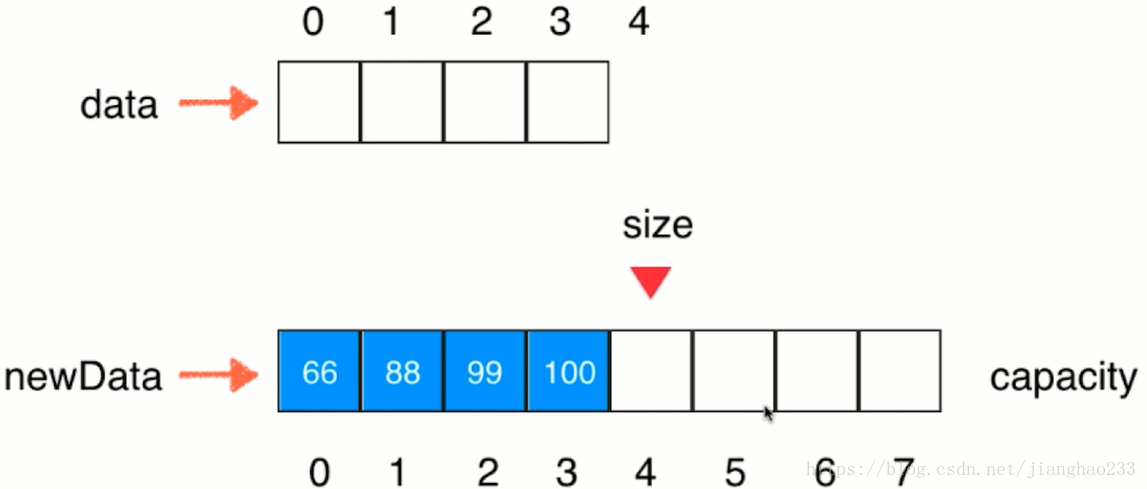
将数组data的引用改为指向 新的有8个空间的数组，与newData的引用相同,指向同样的空间；整个过程封装在函数中，当函数执行完成后，newData 就会失效了；而 data 是整个类的成员变量，和整个类的成员变量是相同的，只要类在使用则data就是有效的；
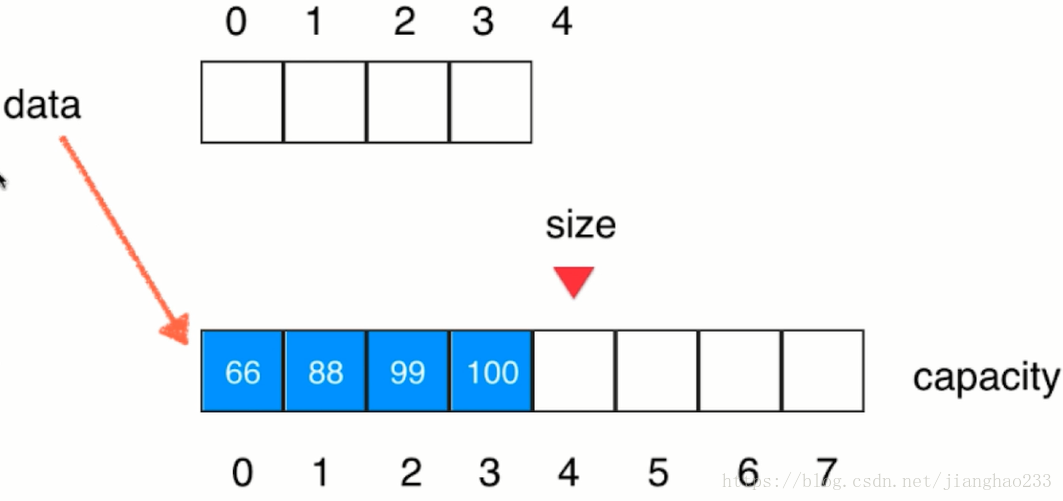
之前的4个空间的数组，因为已经没有引用了，垃圾回收器会将其销毁；数组完成扩容
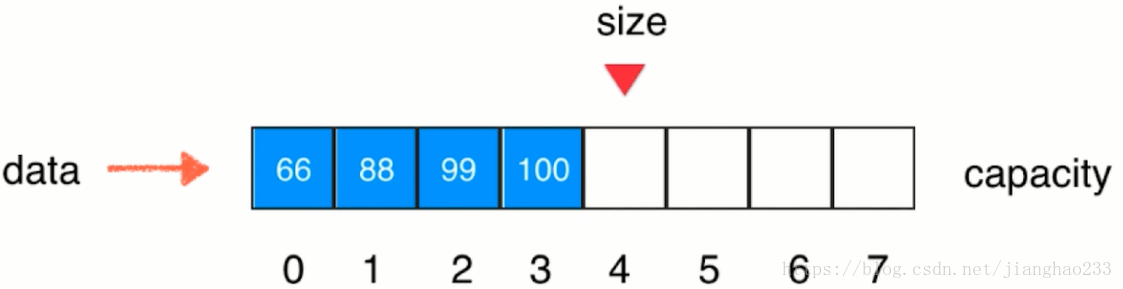
示例代码：Array.java
public class Array<E> {
private E[] data;
private int size;
// 构造函数，传入数组的容量capacity构造Array
public Array(int capacity){
data = (E[])new Object[capacity];
size = 0;
}
// 无参数的构造函数，默认数组的容量capacity=10
public Array(){
this(10);
}
// 获取数组的容量
public int getCapacity(){
return data.length;
}
// 获取数组中的元素个数
public int getSize(){
return size;
}
// 返回数组是否为空
public boolean isEmpty(){
return size == 0;
}
// 在index索引的位置插入一个新元素e
public void add(int index, E e){
if(index < 0 || index > size)
throw new IllegalArgumentException("Add failed. Require index >= 0 and index <= size.");
if(size == data.length)
resize(2 * data.length); //（新增代码）进行数组扩容，变为原来的2倍
for(int i = size - 1; i >= index ; i --)
data[i + 1] = data[i];
data[index] = e;
size ++;
}
// 向所有元素后添加一个新元素
public void addLast(E e){
add(size, e);
}
// 在所有元素前添加一个新元素
public void addFirst(E e){
add(0, e);
}
// 获取index索引位置的元素
public E get(int index){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Get failed. Index is illegal.");
return data[index];
}
// 修改index索引位置的元素为e
public void set(int index, E e){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Set failed. Index is illegal.");
data[index] = e;
}
// 查找数组中是否有元素e
public boolean contains(E e){
for(int i = 0 ; i < size ; i ++){
if(data[i].equals(e))
return true;
}
return false;
}
// 查找数组中元素e所在的索引，如果不存在元素e，则返回-1
public int find(E e){
for(int i = 0 ; i < size ; i ++){
if(data[i].equals(e))
return i;
}
return -1;
}
// 从数组中删除index位置的元素, 返回删除的元素
public E remove(int index){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Remove failed. Index is illegal.");
E ret = data[index];
for(int i = index + 1 ; i < size ; i ++)
data[i - 1] = data[i];
size --;
data[size] = null; // loitering objects != memory leak
if(size == data.length / 2) //新增代码，当数组中实际使用的空间为一半时[size 是 capacity 的一半]
resize(data.length / 2); //使数组变为当前设置数组容量的一半
return ret;
}
// 从数组中删除第一个元素, 返回删除的元素
public E removeFirst(){
return remove(0);
}
// 从数组中删除最后一个元素, 返回删除的元素
public E removeLast(){
return remove(size - 1);
}
// 从数组中删除元素e
public void removeElement(E e){
int index = find(e);
if(index != -1)
remove(index);
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
res.append(String.format("Array: size = %d , capacity = %d\n", size, data.length));
res.append('[');
for(int i = 0 ; i < size ; i ++){
res.append(data[i]);
if(i != size - 1)
res.append(", ");
}
res.append(']');
return res.toString();
}
// （新增代码）将数组空间的容量变成newCapacity大小（2倍）
private void resize(int newCapacity){
E[] newData = (E[])new Object[newCapacity]; //new 一个新的E型数组newData
for(int i = 0 ; i < size ; i ++)
newData[i] = data[i]; //将原来的数组内容放入到新的newData中
data = newData; //让 data 指向 newData 的空间
}
}
Main.java
public class Main {
public static void main(String[] args) {
Array<Integer> arr = new Array<>();//修改代码，（）中不填容量大小，使用默认容量
for(int i = 0 ; i < 10 ; i ++)
arr.addLast(i);
System.out.println(arr);
arr.add(1, 100);
System.out.println(arr);
arr.addFirst(-1);
System.out.println(arr);
arr.remove(2);
System.out.println(arr);
arr.removeElement(4);
System.out.println(arr);
arr.removeFirst();
System.out.println(arr);
}
}
输出：
2.复杂度分析
时间复杂度分析：例：O(1)、O(n)、O(lgn)、O(nlogn)、O(n^2)
O:描述的是算法的运行时间和输入数据之间的关系
上图中：c1指【for 循环中，将nums这个数取出来、将sum这个数取出来、将sum和nums 加在一起、最后将结果扔回给sum变量】这些操作花费的总时间；实际中无法具体取得
c2指【在整个程序中，开辟 Int 型空间 sum，并将0的初始化空间赋值给 sum,在运算结束后，还有返回sum】这些操作花费的总时间；实际中无法具体取得
前两个忽略常数，都是O(n),虽然第三个的常数值很小，但它还是O(n^2),但并不代表：对于任意输入来说，O(n)都要优于O(n^2)，O 是渐进时间复杂度，【描述 n 趋近于无穷的情况来比较算法的性能】；最后一个中，低阶的300n 相比 n^2(高阶)可忽略，故为O(n^2)；
3.动态数组的时间复杂度分析
添加操作：通常情况下（按最坏的情况看）是 O(n)
addLast(e) ---O(1) :该操作所消耗时间与数据规模没有关系，无论数组中有多少元素，addLast都能在常数时间内完成。
addFirst(e) ---O(n) :数组头添加元素需要将数组每个元素向后移动一个单位，故为O(n)。
add(index,e) --O(n/2)=O(n) :在数组 index 索引的位置插入元素e，时间复杂度与 index 相关，index = 0时和addFirst(e)相同；index = size时和addLast(e)相同，分析：假设多种情况下的概率相同，运用概率论的知识，求出时间的期望。平均来看需要右移动 n/2 个元素，O需要忽略常数，故为 O(n)。
删除操作：通常情况下（按最坏的情况看）是 O(n)
removeLast(e) ---O(1)
removeFirst(e) ---O(n)
remove(index,e) --- O(n/2)=O(n)
resize ---O(n)
修改操作：已知索引：O(1) 数组最大优势--支持随机访问，只要知道索引就可以马上访问到该数据
未知索引：O(n) 需要从头遍历数组来找到该元素进行修改
set(index,e) ---O(1)
查找操作：需要从头遍历数组来找到该元素
get(index) ---O(1) 知道所要查找元素的索引，立马可以拿到该值
contains(e) --- O(n) 不知道所要查找元素的索引，查看数组中是否包含某个元素
find(e) ---O(n) 不知道所要查找元素的索引，查看数组中 e 元素对应的索引是多少
4.均摊复杂度和防止复杂度的震荡
resize 的时间复杂度分析
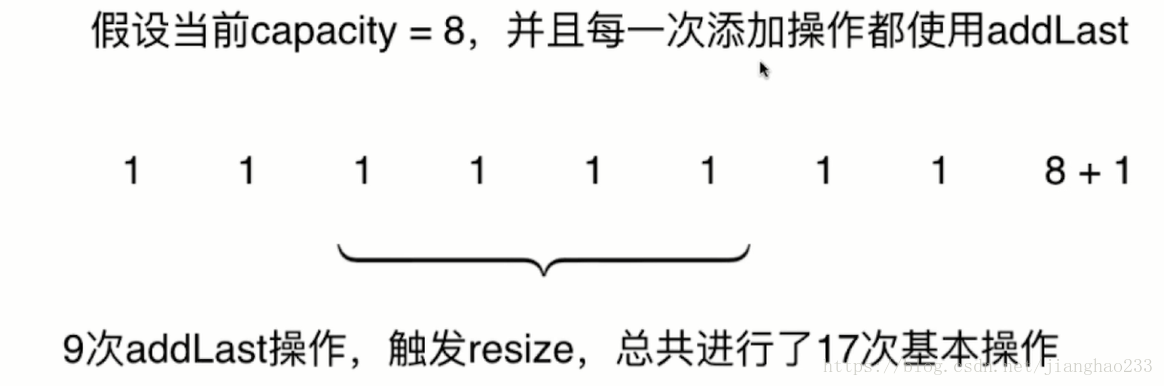
因为最坏的情况（resize）要在很多次 addLast 操作后才会执行； 运用均摊复杂度比较合适；
addLast 和 removeLast 的均摊复杂度均为O(1);
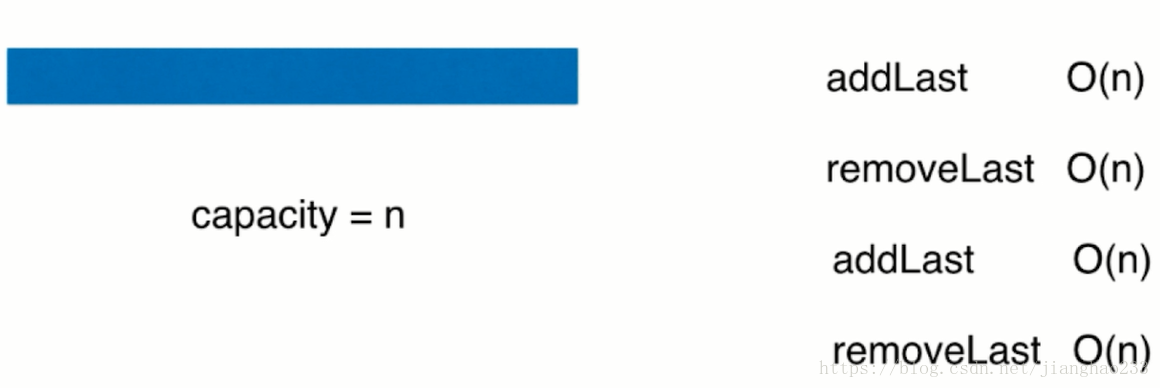
复杂度震荡
上面的那种所说的是大多数情况下，都不会执行resize,现在认为制造这样的情景，让 addLast 和 removeLast 依次执行多次，这样就会每次都执行 resize ，addLast 和 removeLast 的时间复杂度均为O(n);从O(1)变为O(n)，产生复杂度震荡
解决复杂度震荡问题：
出现原因：removeLast 时 resize 过于着急
解决方案：设置 resize == capacity/4 时，才将 capacity 减半
图解过程：
1.添加元素超过 size ,容量扩大一倍
2.删除元素后，先不着急缩小数组容量
3.等到数组长度size缩小到数组容量capacity 的1/4 时
4.缩小数组容量，但也只缩小到原来的一半，仍然预留了一半的数组容量供数组进行 addLast 操作
示例代码：Array.java
public class Array<E> {
private E[] data;
private int size;
// 构造函数，传入数组的容量capacity构造Array
public Array(int capacity){
data = (E[])new Object[capacity];
size = 0;
}
// 无参数的构造函数，默认数组的容量capacity=10
public Array(){
this(10);
}
// 获取数组的容量
public int getCapacity(){
return data.length;
}
// 获取数组中的元素个数
public int getSize(){
return size;
}
// 返回数组是否为空
public boolean isEmpty(){
return size == 0;
}
// 在index索引的位置插入一个新元素e
public void add(int index, E e){
if(index < 0 || index > size)
throw new IllegalArgumentException("Add failed. Require index >= 0 and index <= size.");
if(size == data.length)
resize(2 * data.length);
for(int i = size - 1; i >= index ; i --)
data[i + 1] = data[i];
data[index] = e;
size ++;
}
// 向所有元素后添加一个新元素
public void addLast(E e){
add(size, e);
}
// 在所有元素前添加一个新元素
public void addFirst(E e){
add(0, e);
}
// 获取index索引位置的元素
public E get(int index){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Get failed. Index is illegal.");
return data[index];
}
// 修改index索引位置的元素为e
public void set(int index, E e){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Set failed. Index is illegal.");
data[index] = e;
}
// 查找数组中是否有元素e
public boolean contains(E e){
for(int i = 0 ; i < size ; i ++){
if(data[i].equals(e))
return true;
}
return false;
}
// 查找数组中元素e所在的索引，如果不存在元素e，则返回-1
public int find(E e){
for(int i = 0 ; i < size ; i ++){
if(data[i].equals(e))
return i;
}
return -1;
}
// 从数组中删除index位置的元素, 返回删除的元素
public E remove(int index){
if(index < 0 || index >= size)
throw new IllegalArgumentException("Remove failed. Index is illegal.");
E ret = data[index];
for(int i = index + 1 ; i < size ; i ++)
data[i - 1] = data[i];
size --;
data[size] = null; // loitering objects != memory leak
if(size == data.length / 4 && data.length / 2 != 0)
//(修改代码，数组长度size为数组容量1/4时才会缩小数组容量)
resize(data.length / 2);
return ret;
}
// 从数组中删除第一个元素, 返回删除的元素
public E removeFirst(){
return remove(0);
}
// 从数组中删除最后一个元素, 返回删除的元素
public E removeLast(){
return remove(size - 1);
}
// 从数组中删除元素e
public void removeElement(E e){
int index = find(e);
if(index != -1)
remove(index);
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
res.append(String.format("Array: size = %d , capacity = %d\n", size, data.length));
res.append('[');
for(int i = 0 ; i < size ; i ++){
res.append(data[i]);
if(i != size - 1)
res.append(", ");
}
res.append(']');
return res.toString();
}
// 将数组空间的容量变成newCapacity大小
private void resize(int newCapacity){
E[] newData = (E[])new Object[newCapacity];
for(int i = 0 ; i < size ; i ++)
newData[i] = data[i];
data = newData;
}
}
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
