本文详细解析了1x1卷积核在深度学习中的应用，包括跨通道信息交互、降维升维及增加非线性特性。通过实例展示了如何在不改变图片尺寸的情况下，有效调整特征维数，优化网络结构。
c参考：
https://blog.youkuaiyun.com/ybdesire/article/details/80314925
之前说错了，今天更正一下，1*1的卷积核参数是4维的1*1*intput_channel*ouput_channel。
类似全连接。
最近在看Google的Inception、Resnet以及一些最新的CNN网络时发现其中常常用到1*1的卷积核，一直不太明白这样不就是复制前一层网络信息吗？
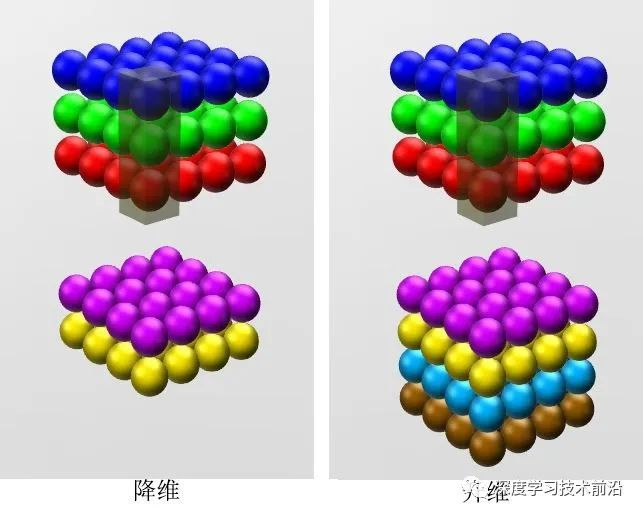
后来发现1*1卷积真的很有用。对于一张图片28*28*1这样的单通道图片，其的确没什么作用。但是如果对于28*28*16中多通道图片，使用6个1*1*16的卷积核之后可以将其压缩成28*28*6，也就是图片高和宽不变，改变了特征维数。
28*28*16 与1*1*16进行卷积，得到28*28*1。
与这个基本一致
好处1：Inception中使用1*1卷积核，可以在某种程度上可以减少运算次数，同时不减少精度。
好处2：Resnet中的block先会使用1*1降维 3*3 之后 再1*1 升维，保证输出和前一层输入维数一致。
所谓信道压缩，Network in Network是怎么做到的？
对于如下的二维矩阵，做卷积，相当于直接乘以2，貌似看上去没什么意义。
但是，对于下面这种32通道的数据，如果我用1个1x1x32的卷积核与其做卷积运算，得到的就是1个6x6的矩阵。
在这个过程中，发生了如下的事情：
（1）遍历36个单元格（6x6）
（2）计算左图中32个信道中截面与卷积核中32个元素的乘积
（3）此时得到的结果，仍然是6x6x32的矩阵
（4）每个6x6的矩阵都叠加起来，得到一个6x6的矩阵
（5）接下来用Relu函数作用于这个6x6的矩阵
（6）得到6x6的输出
同理，如果我用N个1x1x32的卷积核与其做卷积运算，得到的就是N个6x6的矩阵。
所以，1x1的卷积，可以从根本上理解为：有一个全连接的神经网络，作用在了不同的32个位置上。
这种做法，通常称为1x1卷积或Network in Network。它的主要作用，就是降低信道数量。如下图
28x28x192的数据，被32个1x1x192的卷积核作用后，就变为28x28x32的数据。这也就是所谓信道压缩，信道降维。当然如果你愿意，也可以增加信道维度。这在Inception网络中很有用。
1*1的卷积结果，每个featuremap上的特征的线性变换，是liner在多维的扩展。
liner只能是二维的线性变换，1*1的卷积是多维的线性变换，也叫全连接。
下面是验证代码：
padding=1，则会产生8*8*10的featuremap
padding=0，则会产生6*6*10的featuremap
对于1*6*6*20的输入，输出是1*10*6*6，参数量是10*20*1*1
import torch
x = torch.randn(1,20,6, 6) # 输入的维度是（128，20）
conv1 = nn.Conv2d(in_channels=20, out_channels=10, kernel_size=1, stride=1, padding=0, bias=True)
output = conv1(x)
print('m.weight.shape: ', conv1.weight.shape)
print('m.bias.shape:', conv1.bias.shape)
print('output.shape:', output.shape)
1x1卷积的作用：
1x1卷积的作用可以总结为以下三点：
-
可以实现信息的跨通道整合和交互
-
具有降维和升维的能力，减少网络参数。这里的维度指的是卷积核通道数（厚度），而不改变图片的宽和高。
-
在保持feature map 尺寸不变（即不损失分辨率）的前提下大幅增加非线性特性，既可以把网络做得很deep，也可以提升网络的表达能力
跨通道信息交互(channel)
例子：使用1x1卷积核，实现降维和升维的操作其实就是channel间信息的线性组合变化，3x3，64channels的卷积核后面添加一个1x1，28channels的卷积核，就变成了3x3，28channels的卷积核，原来的64个channels就可以理解为跨通道线性组合变成了28channels，这就是通道间的信息交互。
注意：只是在channel维度上做线性组合，W和H上是共享权值的sliding window
降维/升维
在卷积神经网络中，channels 的含义一般是指每个卷积层中卷积核的数量。
1×1卷积核并不会改变 height 和 width，改变通道的第一个最直观的结果，就是可以将原本的数据量进行增加或者减少。这里通常都称之为升维、降维。而且改变的只是 height × width × channels 中的 channels 这一个维度的大小而已。
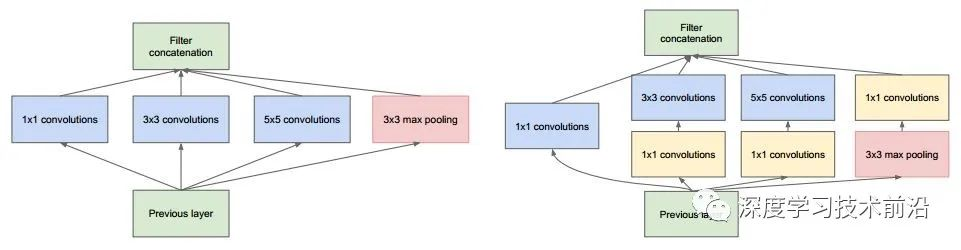
这里我们以GoogLeNet的3a模块为例，输入的feature map是28×28×192，3a模块中1×1卷积通道为64，3×3卷积通道为128,5×5卷积通道为32，如果是左图结构，那么卷积核参数为1×1×192×64+3×3×192×128+5×5×192×32，
而右图对3×3和5×5卷积层前分别加入了通道数为96和16的1×1卷积层，这样卷积核参数就变成了：1×1×192×64+（1×1×192×96+3×3×96×128）+（1×1×192×16+5×5×16×32），参数大约减少到原来的三分之一。
同时在并行pooling层后面加入1×1卷积层后也可以降低输出的feature map数量，(feature map尺寸指W、H是共享权值的sliding window，feature map 的数量就是channels）
左图pooling后feature map是不变的，再加卷积层得到的feature map，会使输出的feature map扩大到416，如果每个模块都这样，网络的输出会越来越大。
而右图在pooling后面加了通道为32的1×1卷积，使得输出的feature map数降到了256。GoogLeNet利用1×1的卷积降维后，得到了更为紧凑的网络结构，虽然总共有22层，但是参数数量却只是8层的AlexNet的十二分之一（当然也有很大一部分原因是去掉了全连接层）
增加非线性
在CNN里的卷积大都是多通道的feature map和多通道的卷积核之间的操作（输入的多通道的feature map和一组卷积核做卷积求和得到一个输出的feature map），如果使用1x1的卷积核，这个操作实现的就是多个feature map的线性组合，可以实现feature map在通道个数上的变化。
备注：一个filter对应卷积后得到一个feature map，不同的filter(不同的weight和bias)，卷积以后得到不同的feature map，提取不同的特征，得到对应的specialized neuro。
扫一扫
3815
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
