雾
模拟雾的方法有很多种,从非常简单的模型到包含光散射效应的复杂模型。即使非常简单的方法也是有效的。有一种方法是基于物体距眼睛的距离将实际像素颜色与另一种颜色(“雾”的颜色通常是灰色或蓝灰色——也用于背景颜色)混合。
下图说明了这个概念。眼睛(相机)显示在左侧,两个红色物体放置在视锥体中。圆柱体更靠近眼睛,所以它主要是原始颜色(红色);立方体远离眼睛,所以它主要是雾色。对于这个简单的实现,几乎所有的计算都可以在片段着色器中执行。

下面程序显示了一个非常简单的雾算法的相关代码,该算法按照从相机到像素的距离,使用从对象颜色到雾颜色的线性混合。具体来说,此示例将雾添加到以前程序“✠OpenGL-10-增强表面细节”中的高度贴图示例。
// 顶点着色器
#version 430
...
out vec3 vertEyeSpacePos;
...
// 在视觉空间中不考虑透视计算顶点位置,并将它发送给片段着色器
// 变量 p 是高度贴图后的顶点,正如“✠OpenGL-10-增强表面细节”中所述
vertEyeSpacePos = (mv_matrix * p).xyz;
// 片段着色器
#version 430
...
in vec3 vertEyeSpacePos;
out vec4 fragColor;
...
void main() {
vec4 fogColor = vec4(0.7, 0.8, 0.9, 1.0);// 蓝灰色
float fogStart = 0.2;
float fogEnd = 0.8;
// 在视觉空间中从摄像机到顶点的距离就是到这个顶点的向量的长度,
// 因为摄像机在视觉空间中的(0,0,0)位置
float dist = length(vertEyeSpacePos.xyz);
float fogFactor = clamp((fogEnd-dist)/(fogEnd-fogStart), 0.0, 1.0);
fragColor = mix(fogColor, texture(t, tc), fogFactor);
}
GLSL 的 clamp()函数用于将此比率限制在值 0.0 和 1.0 之间。然后, GLSL 的 mix()函数根据 fogFactor 的值返回雾颜色和对象颜色的加权平均值。
genFType clamp(genFType x, genFType minVal, genFType maxVal)
返回:min(max(x, minVal), maxVal)。即保证了结果在[minVal,maxVal]区间,如果x本来就在此区间则值不变。
如果minVal > maxVal,结果是未知的。
genFType mix(genFType x, genFType y, genFType a)
返回:x与y的线性混合,例如 x·(1-a)+y·a;a从0变到1,就是从x变到y的过程。
令dis<=0.2,则fogFactor=1,fragColor=texture(t,tc),即像素不在雾中,像素颜色就是纹理的颜色。
令dist=0.7,则(0.8-0.7)/(0.8-0.2)=0.17,所以fogFactor=0.17,fragColor=0.83×fogColor+0.17×texture(t,tc),即像素颜色接近雾的颜色。
令dist>=0.8,则fogFactor=0,fragColor=fogColor,即像素颜色就是雾颜色,看不到像素了。

复合、混合、透明度
回忆一下“✠OpenGL-2-图像管线”,像素操作利用 Z 缓冲区,当发现另一个对象在该像素的位置更近时,通过替换现有的像素颜色来实现隐藏面消除。我们实际上可以更好地控制这个过程——可以选择混合两个像素。
当渲染一个像素时,它被称为“源”像素。已经在帧缓冲器中的像素(可能是从先前的对象渲染得来)被称为“目标”像素。 OpenGL 提供了许多选项,用于决定最终将两个像素中的哪一个或者它们的组合,放置在帧缓冲区中。请注意,像素操作步骤不是可编程阶段——因此用于配置所需合成的 OpenGL 工具可在 C++应用程序中(而不是在着色器中)找到。
用于控制合成的两个 OpenGL 函数是 glBlendEquation(mode)和 glBlendFunc(srcFactor, destFactor)。下图显示了合成过程的概述。

void glBlendEquation(GLenum mode)
指定像素算法。(blend: /blend/ 混合、融合)
mode - 指定如何组合源颜色和目标颜色。
可接受的常量: GL_FUNC_ADD, GL_FUNC_SUBTRACT, GL_FUNC_REVERSE_SUBTRACT, GL_MIN, GL_MAX
RGB混合方程和alpha混合方程,初始值都为GL_FUNC_ADD。
混合方程确定新像素(“源”颜色)如何与帧缓冲区中已有的像素(“目标”颜色)组合。此函数用于将RGB混合方程和alpha混合方程设置为单个方程。
void glBlendFunc(GLenum sfactor, GLenum dfactor)
指定用于RGB混合方程和Alpha混合方程的方程。
sfactor - 指定如何计算红色、绿色、蓝色和alpha源混合因子。初始值为GL_ONE。
dfactor - 指定如何计算红色、绿色、蓝色和alpha目标混合因子。初始值为GL_ZERO。
混合默认是禁用的。
所有比例因子的范围均为[0,1]。
可以使用将传入(源)RGBA值与帧缓冲区中已有的RGBA值(目标值)混合的函数来绘制像素。

那些用到“blendColor”的选项需要额外调glBlendColor()来指定将用于计算混合函数结果的常量颜色。还有一些其他混合函数未在表中显示。
合成过程:
(1)首先,源像素和目标像素分别乘以由混合函数 blendFunc()指定的源因子和目标因子。
(2)然后,使用混合方程函数 blendEquation()来组合修改后的源像素和目标像素以生成新的目标颜色。
glBlendFunc()默认设置 srcFactor 为 GL_ONE(1.0),destFactor 为 GL_ZERO(0.0);glBlendEquation()的默认值为 GL_FUNC_ADD。
因此,在默认情况下,源像素不变(乘以 1),目标像素被按比例缩小到 0,并且两者相加意味着源像素变为帧缓冲区的颜色。
还有命令 glEnable(GL_BLEND)和 glDisable(GL_BLEND)(默认是禁用的),它们可用于告诉 OpenGL 应用指定的混合,或忽略它。
我们不会在这里说明所有选项的效果,但我们将介绍一些说明性示例。假设我们在C++/OpenGL 应用程序中指定以下设置:
glEnable(GL_BLEND);// 启用混合
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
glBlendEquation(GL_FUNC_ADD);
合成将如下进行:
(1)源像素按其 Alpha 值缩放。
(2)目标像素按 1−srcAlpha(源透明度)缩放。
(3)像素值加在一起。
例如,如果源像素为红色,具有 75%不透明度,即[1,0,0,0.75],并且目标像素包含完全不透明的绿色,即[0,1,0,1],则结果放在帧缓冲区将是:
srcPixel * srcAlpha = [0.75, 0, 0, 0.5625]
destPixel * (1-srcAlpha) = [0, 0.25, 0, 0.25]
resulting pixel = [0.75, 0.25, 0, 0.8125]
也就是说,主要是红色,有些是绿色的,而且基本上是实色。这个设置的总体效果是让目标像素以与源像素的透明度相对应的量显示。在此示例中,帧缓冲区中的像素为绿色,输入像素为红色,透明度为 25%(不透明度为 75%)。因此允许一些绿色通过红色显示。
glEnable(GL_BLEND)的一个更简单直观的理解,见我的另一篇Bog:◮OpenGL-混合
一个示例:
事实证明,混合函数和混合方程的这些设置在许多情况下都能很好地工作。我们将它们应用到包含两个 3D 模型的场景中的实际示例中去:一个环面和环面前的金字塔。下图显示了这样一个场景,左边是一个不透明的金字塔,右边是金字塔的 Alpha 值设置为 0.8。光照已经添加。

上面效果存在相当明显的不足之处。尽管金字塔模型现在实际上是透明的,但实际透明的金字塔不仅应该显示其背后的对象,还应该显示其自身的背面。
实际上,金字塔的背面没有出现的原因是因为我们启用了背面剔除。一个合理的想法可能是在绘制金字塔时禁用背面剔除。但是,这通常会产生其他伪影,如下图所示。简单地禁用背面剔除的问题在于混合的效果取决于渲染表面的顺序(因为这决定了源像素和目标像素),并且我们不总是能够控制渲染顺序。通常有利的是首先渲染不透明对象,以及在后面的对象(例如环面),最后再渲染透明对象。这也适用于金字塔的表面,并且在这种情况下,包括金字塔底部的两个三角形看起来不同的原因是它们中的一个在金字塔的前面之前被渲染而一个在之后被渲染。诸如此类的伪影有时被称为“顺序”伪影,并且它们可以在透明模型中显示,因为我们不总是能预测其三角形将被渲染的顺序。

我们可以通过从背面开始分别渲染正面和背面来解决金字塔示例中的问题。下面程序显示了执行此操作的代码。我们通过统一变量来指定金字塔的 Alpha 值并传递给着色器程序,然后通过将指定的 Alpha 替换为计算的输出颜色将其应用于片段着色器中。
请注意,要使光照正常工作,我们必须在渲染背面时翻转法向量。我们通过向顶点着色器发送一个标志来完成此操作,然后我们在其中翻转法向量。
void display() {
// 【先】正常完成绘制圆环
...
aLoc = glGetUniformLocation(renderingProgram, "alpha");
fLoc = glGetUniformLocation(renderingProgram, "flipNormal");
...
glEnable(GL_CULL_FACE);
...
glEnable(GL_BLEND);// 启用混合
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);// 指示OpenGL:要完全混合
glBlendEquation(GL_FUNC_ADD);// 指示OpenGL:要完全混合
glCullFace(GL_FRONT);// 剔除前面,即【先渲染金字塔的背面】
glProgramUniform1f(renderingProgram, aLoc, 0.3f);// 背面非常透明
glProgramUniform1f(renderingProgram, fLoc, -1.0f);// 翻转背面的法向量,传递一个小于0的标志值
glDrawArrays(GL_TRIANGLES, 0, numPyramidVertices);
glCullFace(GL_BACK);// 剔除背面,【然后渲染金字塔的正面】
glProgramUniform1f(renderingProgram, aLoc, 0.7f);// 正面略微透明
glProgramUniform1f(renderingProgram, fLoc, 1.0f);// 正面不需要翻转法向量,传递一个大于0的标志值
glDrawArrays(GL_TRIANGLES, 0, numPyramidVertices);
glDisable(GL_BLEND);// 还原为禁用混合
}
// 顶点着色器
#version 430
...
if (flipNormal < 0)
varyingNormal = -varyingNormal;
...
// 片段着色器
#version 430
uniform float alpha;
...
fragColor = globalAmbient*material.ambient + ... etc.// 和Blinn-Phone光照一样
fragColor = vec4(fragColor.xyz, alpha);// 使用统一变量发送的alpha值替换
这种“两遍校正”解决方案的结果如下图:

虽然它在这里运行良好,但上述程序中显示的两遍解决方案并不总是足够的。例如,一些更复杂的模型可能具有面向前方的隐藏表面,并且如果这样的对象变得透明,我们的算法将无法渲染模型的那些隐藏的前向部分。 Alec Jacobson 描述了一个适用于大量案例的五遍序列[A. Jacobson, “Cheap Tricks for OpenGL Transparency,” 2012, accessed October 2018.]。
程序理解:
因为像素操作步骤不是可编程阶段,所以我们在C++/OpenGL程序中指示在像素操作阶段之前,完成指定参数的像素混合操作,然后放置在帧缓冲区中。
假设原来绘制的第1个模型的某像素在帧缓冲区中的颜色为红色(目标像素destPixel),现在绘制第2个模型,模型上对应的某像素颜色为绿色(源像素srcPixel),如果调用函数为glBlendFunc(GL_SRC_COLOR, GL_DEST_COLOR); glBlendEquation(GL_FUNC_ADD); 则最终写到帧缓冲区的新颜色值为:srcPixelRGBA×srcPixelRGBA + destPixelRGBA×destPixelRGBA,最终呈现出的颜色就是红色和绿色的混合色(黄色)。
如果glDisable(GL_BLEND); 不启用混合,则相当于默认的glBlendFunc(GL_ONE, GL_ZERO); glBlendEquation(GL_FUNC_ADD); 即srcFactor=(1,1,1,1)、destFactor=(0,0,0,0),最终写到帧缓冲区的新颜色值为:srcPixelRGBA,即最终呈现的颜色就是源像素颜色(红色)。
应该可以理解为,从片段着色器输出的颜色就是源片段(像素)的颜色,已经在帧缓冲区的像素就是目标像素,混合的最终处理阶段是在后续管线的像素混合阶段这个不可编程阶段完成的。可以理解为当我们glEnable(GL_BLEND)功能,设置好glBlendFunc函数后,就表示:相比于之前绘制的物体,在之后绘制的物体将最终生成与之前物体混合的效果。
如果没有混合操作,则下图(左)中圆圈框出的部分就不会有两个物体混合的效果;如果禁用混合,并把alpha值设置为0,效果如下图(右):

可以看到,禁用混合后,即使透明度硬编码为0(fragColor = vec4(fragColor.xyz, 0);)两个物体都不会有任何透明效果,即直接在片段着色器中设置片段的alpha值是无效的,它总保持为1。
用户定义剪裁平面
OpenGL 不仅可以应用于视锥体,还包括了指定剪裁平面的功能。用户定义的剪裁平面的一个用途是对模型切片。这样就可以通过从简单的模型开始并从中切片来创建复杂的形状。
剪裁平面使用平面的标准数学定义来定义:ax + by + cz + d = 0
其中 a、b、c 和 d 是用来定义 XYZ 的 3D 空间中特定平面的参数。参数表示垂直于平面的向量(a,b,c),以及从原点到平面的距离 d。
可以使用 vec4 在顶点着色器中指定这样的平面,如下所示:
vec4 clip_plane = vec4(0.0, 0.0, -1.0, 0.2); 对应于平面:(0.0) x + (0.0) y + (-1.0) z + 0.2 = 0
然后,通过使用内置的 GLSL 变量 gl_ClipDistance[],可以在 [顶点着色器] 中实现裁剪,如下例所示:
gl_ClipDistance[0] = dot(clip_plane.xyz, vertPos) + clip_plane.w;
其中,vertPos 指的是在顶点属性(例如来自 VBO)中进入顶点着色器的顶点位置, clip_plane 定义如上。然后我们计算从裁剪平面到传入顶点的带符号距离clip_plane.w,如果顶点在平面上,则为 0,或者取决于顶点在平面的哪一侧而为负或正。
gl_ClipDistance 数组的下标允许定义多个裁剪距离(即多个平面)。可以定义的最大用户裁剪平面数量取决于图形卡的 OpenGL 实现。
然后必须在 C++/OpenGL 应用程序中启用用户定义的裁剪。内置 OpenGL 标识符GL_CLIP_DISTANCE0、 GL_CLIP_DISTANCE1 等,对应于每个 gl_ClipDistance[ ]数组元素。
例如,启用第 0 个用户定义剪裁平面:glEnable(GL_CLIP_DISTANCE0);
将前面的步骤应用到我们的发光环面会产生如下图所示的输出, 其中环面的前半部分已经被剪裁了(还应用了旋转以提供更清晰的视图)。
可能看起来好像环面的底部也被修剪了,但这是因为环面的内表面没有被渲染。当裁剪会显示形状的内部表面时,也就需要渲染它们,否则模型将显示得不完整。

渲染内表面需要再次调用 gl_DrawArrays(),并颠倒缠绕顺序。此外,在渲染背向三角形时,必须反转曲面法向量。
void display() {
...
flipLoc = glGetUniformLocation(renderingProgram, "flipNormal");
...
glEnable(GL_CLIP_DISTANCE0);// 启用第 0 个用户定义剪裁平面
// 正常绘制外表面
glUniform1i(flipLoc, 0);
glFrontFace(GL_CCW);
glDrawElements(GL_TRIANGLES, numTorusIndices, GL_UNSIGNED_INT, 0);
// 渲染背面,法向量反转
glUniform1i(flipLoc, 1);
glFrontFace(GL_CW);
glDrawElements(GL_TRIANGLES, numTorusIndices, GL_UNSIGNED_INT, 0);
}
// 顶点着色器
#version 430
...
vec4 clip_plane = vec4(0.0, 0.0, -1.0, 0.5);
uniform int flipNormal;// 反转法向量的标志
...
void main() {
...
if (flipNormal == 1)
varyingNormal = -varyingNormal;
...
// 计算从裁剪平面到传入顶点的带符号距离
gl_ClipDistance[0] = dot(clip_plane.xyz, vertPos) + clip_plane.w;
...
}

void glDepthRange(GLdouble nearVal, GLdouble farVal)
指定从标准化设备坐标到窗口坐标的深度值映射。
nearVal - 指定近剪裁平面到窗口坐标的映射。初始值为0。
farVal - 指定远剪裁平面到窗口坐标的映射。初始值为1。
剪裁并除以w后,深度坐标的范围为−1到1,对应于近剪裁平面和远剪裁平面。glDepthRange指定此范围内的规范化深度坐标到窗口深度坐标的线性映射。不管实际的深度缓冲区实现如何,窗口坐标深度值都被视为从0到1的范围(类似于颜色组件)。因此,glDepthRange接受的值在被接受之前都被钳制在这个范围内。
(0,1) 的设置将近平面映射为0,远平面映射为1。通过此映射,深度缓冲区范围得到充分利用。
void glClipControl(GLenum origin, GLenum depth)
控制裁剪坐标到窗口坐标的行为。
origin - 指定裁剪控件的原点。必须是GL_LOWER_LEFT 或 GL_UPPER_LEFT。
depth - 指定裁剪控制的深度模式。必须是GL_NEGATIVE_ONE_TO_ONE 或 GL_ZERO_TO_ONE。
默认的GL裁剪体:origin=GL_LOWER_LEFT,depth=GL_NEGATIVE_ONE_TO_ONE
origin=GL_LOWER_LEFT:裁剪空间x,y坐标(-1,-1)对应窗口左上角,因为y轴正向对应窗口空间的下方向。
depth设置的是剪切空间深度值映射到glDepthRange()所设置的数值的方式。默认窗口空间深度值区间为[0,1]。
depth=GL_NEGATIVE_ONE_TO_ONE:negative1 to 1,窗口空间深度值[0,1]默认对应于裁剪空间的[-1,1];
depth=GL_ZERO_TO_NOE:0 to 1,窗口空间深度值[0,1]默认对应于裁剪空间的[0,1]。
剪裁空间的z负值将被处于近平面后方。
OpenGL默认是GL_NEGATIVE_ONE_TO_ONE,即映射的深度区间是[-1.0, 1.0]。
通过glClipControl(GL_LOWER_LEFT, GL_ZERO_TO_ONE)可以修改为[0, 1.0]。修改后可以和D3D/Vulkan的默认行为类似,因为3D/Vulkan默认的深度范围是[0.0,1.0]。
3D纹理
2D 纹理包含由两个变量索引的图像数据,而 3D 纹理包含相同类型的图像数据,但是处在由 3 个变量索引的 3D 结构中。前两个维度仍然代表纹理贴图中的宽度和高度,第三个维度代表深度。
建议将 3D 纹理视为一种物质,我们将其浸没(或“浸入”)被纹理化的对象,从而使对象的表面点从纹理中的相应位置获得颜色。 或者可以想象这个物体被从 3D 纹理“立方体” 中“雕刻”出来,就像雕塑家用一块坚固的大理石雕刻出一个人物一样。
3D 纹理通常是在程序上生成的。根据纹理中的颜色,我们可以构建包含这些颜色的三维数组。 如果纹理包含可以与各种颜色一起使用的“图案”,我们可能会建立一个保存图案的数组,例如 0 和 1。
void generate3Dpattern() {
for (int x = 0; x < texWidth; x++) {
for (int y = 0; y < texHeight; y++) {
for (int z = 0; z < texDepth; z++) {
if ((y / 10) % 2 == 0)
tex3Dpattern[x][y][z] = 0.0;
else
tex3Dpattern[x][y][z] = 1.0;
}
}
}
}
以上程序生成存储在tex3Dpattern数组中的图案如下:(0呈蓝色,1呈黄色)

y=[0-9]或[20-29]或[40-49]…时,tex3Dpattern=0;
y=[10-19]或[30-39]或[50-59]…时,tex3Dpattern=1;
从而生成只与y轴相关的蓝黄相间的3D图案。
同样,如果生成3D棋盘纹理,算法如下:
void generate3Dpattern() {
int xStep, yStep, zStep, sumSteps;
for (int x = 0; x < texWidth; x++) {
for (int y = 0; y < texHeight; y++) {
for (int z = 0; z < texDepth; z++) {
xStep = (x / 10) % 2;
yStep = (y / 10) % 2;
zStep = (z / 10) % 2;
sumSteps = xStep + yStep + zStep;
if (sumSteps % 2 == 0)
tex3Dpattern[x][y][z] = 0.0;
else
tex3Dpattern[x][y][z] = 1.0;
}
}
}
}

使用条纹图案对对象进行纹理处理,需要执行以下步骤:
(1) 生成如上图所示的图案;
(2) 使用图案填充所需颜色的字节数组;
(3) 将字节数组加载到纹理对象中;
(4) 确定对象顶点的适当3D纹理坐标;
(5) 在片段着色器中使用适当的采样器来纹理化对象。
3D纹理的纹理坐标范围是[0…1],与2D纹理的方式相同。
在大多数情况下,我们希望对象反映纹理图案,就像它被“雕刻”出来一样(或浸入其中)。所以顶点位置本身就是纹理坐标!通常所需的只是应用一些简单的缩放以确保对象的顶点的位置坐标映射到 3D 纹理坐标的范围[0,1]。
. . .
const int texHeight= 200;
const int texWidth = 200;
const int texDepth = 200;
double tex3Dpattern[texWidth][texHeight][texDepth];// 三维数组,总元素数:texWidth*texHeight*texDepth=8,000,000个
. . .
// 按照由 generate3Dpattern()构建的图案,用蓝色、黄色的 RGB 值来填充字节数组
GLubyte* fillDataArray() {
generate3Dpattern();
GLubyte* data = new GLubyte[texWidth*texHeight*texDepth*4];// 要生成texWidth*texHeight*texDepth*4个元素
for (int i=0; i<texWidth; i++) {
for (int j=0; j<texHeight; j++) {
for (int k=0; k<texDepth; k++) {
if (tex3Dpattern[i][j][k] == 1.0) {
// 黄色
data[(i*(texWidth*texHeight) + j*(texHeight) + k)*4 + 0]=(GLubyte) 255;// red
data[(i*(texWidth*texHeight) + j*(texHeight) + k)*4 + 1]=(GLubyte) 255;// green
data[(i*(texWidth*texHeight) + j*(texHeight) + k)*4 + 2]=(GLubyte) 0;// blue
data[(i*(texWidth*texHeight) + j*(texHeight) + k)*4 + 3]=(GLubyte) 255;// alpha
} else {
// 蓝色
data[(i*(texWidth*texHeight) + j*(texHeight) + k)*4 + 0]=(GLubyte) 0;// red
data[(i*(texWidth*texHeight) + j*(texHeight) + k)*4 + 1]=(GLubyte) 0;// green
data[(i*(texWidth*texHeight) + j*(texHeight) + k)*4 + 2]=(GLubyte) 255;// blue
data[(i*(texWidth*texHeight) + j*(texHeight) + k)*4 + 3]=(GLubyte) 255;// alpha
} } }
return data;
}
// data索引的最大值为:(199*200*200+199*200+199)*4+3=31,999,999 == (200*200*200*4-1)
// 构建条纹的 3D 图案
void generate3Dpattern() {
for (int x=0; x<texWidth; x++) {
for (int y=0; y<texHeight; y++) {
for (int z=0; z<texDepth; z++) {
if ((y/10)%2 == 0)
tex3Dpattern[x][y][z] = 0.0;
else
tex3Dpattern[x][y][z] = 1.0;
} } } }
// 构建棋盘的 3D 图案(替换上面函数即可完成3D棋盘效果)
void generate3DpatternCheckerboard() {
int xStep, yStep, zStep, sumSteps;
for (int x = 0; x < texWidth; x++) {
for (int y = 0; y < texHeight; y++) {
for (int z = 0; z < texDepth; z++) {
xStep = (x / 10) % 2;
yStep = (y / 10) % 2;
zStep = (z / 10) % 2;
sumSteps = xStep + yStep + zStep;
if ((sumSteps % 2) == 0)
tex3Dpattern[x][y][z] = 0.0;
else
tex3Dpattern[x][y][z] = 1.0;
}
}
}
}
// 将顺序字节数据数组加载进纹理对象
int load3DTexture() {
GLuint textureID;
GLubyte* data = fillDataArray();
glGenTextures(1, &textureID);
glBindTexture(GL_TEXTURE_3D, textureID);
glTexParameteri(GL_TEXTURE_3D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
/**
void glTexStorage3D(GLenum target, GLsizei levels, GLenum internalformat,
GLsizei width, GLsizei height, GLsizei depth);
作用:同时为三维、二维阵列或立方体贴图阵列纹理的所有级别指定存储。
*/
glTexStorage3D(GL_TEXTURE_3D, 1, GL_RGBA8, texWidth, texHeight, texDepth);
/**
void glTexSubImage3D(GLenum target, GLint level, GLint xoffset, GLint yoffset, GLint zoffset, GLsizei width,
GLsizei height, GLsizei depth, GLenum format, GLenum type, const void * pixels);
作用:指定三维纹理子图像。
pixels - 指定指向内存中图像数据的指针。
*/
glTexSubImage3D(GL_TEXTURE_3D, 0, 0, 0, 0, texWidth, texHeight, texDepth,
GL_RGBA, GL_UNSIGNED_INT_8_8_8_8_REV, data);
return textureID;
}
void init(GLFWwindow* window) {
. . .
stripeTexture = load3DTexture(); // 为 3D 纹理保存整型图案 ID
}
void display(GLFWwindow* window, double currentTime) {
. . .
glActiveTexture(GL_TEXTURE0);// 激活第0号纹理单元
glBindTexture(GL_TEXTURE_3D, stripeTexture);// 将纹理复制到“3D”纹理单元
glDrawArrays(GL_TRIANGLES, 0, numObjVertices);
}
########################################################
// 顶点着色器
. . .
out vec3 originalPosition;// 原始模型顶点将被用于纹理坐标
. . .
void main(void) {
originalPosition = position;// 将原始模型坐标传递,用作 3D 纹理坐标
gl_Position = proj_matrix * mv_matrix * vec4(position,1.0);
}
// 片段着色器
. . .
in vec3 originalPosition;// 接受原始模型坐标,用作 3D 纹理坐标
out vec4 fragColor;
. . .
layout (binding=0) uniform sampler3D s;// 是`sample3D`而非2D
void main(void) {
// 顶点范围为[−1,+1],转换到纹理坐标范围为[0,1]
fragColor = texture(s, originalPosition / 2.0 + 0.5);
}
应用程序中, load3Dtexture()函数将生成的数据加载到 3D 纹理中。它不使用 SOIL2 来加载纹理,而是直接进行相关的 OpenGL 调用。图像数据应该被格式化为对应于 RGBA 颜色分量的字节序列。函数fillDataArray()执行此操作,应用黄色和蓝色的 RGB 值,依据由 generate3Dpattern()函数构建并保存在 tex3Dpattern 数组中的条带图案。另请注意 display()函数中指定了纹理类型GL_TEXTURE_3D。
由于我们希望将对象的顶点位置用作纹理坐标,我们将它们从顶点着色器传递到片段着色器。片段着色器缩放它们,以便它们按照纹理坐标的标准,被映射到范围[0, 1]。最后,通过 sampler3D 统一变量访问 3D 纹理,该统一变量利用 3 个纹理坐标参数采样而不是两个。我们使用顶点的原始 X、Y 和 Z 坐标,缩放到正确的范围,以访问纹理。结果如下图所示。

如果用棋盘3D纹理,效果如下:

噪声
可以使用随机性或噪声来模拟许多自然现象。一种常见的技术是 Perlin 噪声,它以Ken Perlin 命名。
图形场景中存在许多噪声应用。一些常见的例子是云、地形、木纹、矿产(如大理石中的矿脉)、烟雾、燃烧、火焰、行星表面和随机运动。
包含噪声的空间数据(例如 2D 或 3D)的集合有时被称为噪声图。
#include<random>
...
double noise[noiseWidth][noiseHeight][noiseDepth];
...
void generateNoise() {
for (int x = 0; x < noiseWidth; x++)
for (int y = 0; y < noiseHeight; y++)
for (int z = 0; z < noiseDepth; z++)
noise[x][y][z] = (double) rand() / (RAND_MAX + 1);// 计算出[0...1]范围内的一个double类型数值
}
接下来,fillDataArray()函数,以便将噪声数据复制到字节数组中,以便加载到纹理对象中。
GLubyte* fillDataArray() {
GLubyte* data = new GLubyte[noiseHeight*noiseWidth*noiseDepth * 4];
for (int i = 0; i < noiseWidth; i++) {
for (int j = 0; j < noiseHeight; j++) {
for (int k = 0; k < noiseDepth; k++) {
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+0] = (GLubyte) (noise[i][j][k] * 255);
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+1] = (GLubyte) (noise[i][j][k] * 255);
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+2] = (GLubyte) (noise[i][j][k] * 255);
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+3] = (GLubyte) 25;
}}}
return data;
}
我们令noiseHeight=noiseWidth=noiseDepth=256,其他同前面示例代码,效果如下:

根据用于除法索引的“缩放”因子,可以使得到的 3D 纹理更多或少地呈现“块状”。在下图中,纹理显示了放大的结果,将索引分别除以缩放因子 8、16 和 32(从左到右)。
GLubyte* fillDataArray(GLubyte data[]) {
GLubyte* data = new GLubyte[noiseHeight*noiseWidth*noiseDepth * 4];
int zoom = 8;// 缩放因子
for (int i=0; i<noiseWidth; i++) {
for (int j=0; j<noiseHeight; j++) {
for (int k=0; k<noiseDepth; k++) {
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+0] = (GLubyte) (noise [i/zoom] [j/zoom] [k/zoom] * 255);
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+1] = (GLubyte) (noise [i/zoom] [j/zoom] [k/zoom] * 255);
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+2] = (GLubyte) (noise [i/zoom] [j/zoom] [k/zoom] * 255);
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+3] = (GLubyte) 255;
} } }
return data;
}

通过从每个离散灰度颜色值插值到下一个灰度颜色值,我们可以平滑特定的噪声图内的“块效应”。也就是说,对于给定 3D 纹理内的每个小“块”,我们通过从其颜色到其 相邻块 的颜色进行插值来设置块内的每个纹素的颜色。插值代码在下面所示的函数 smoothNoise()中。下图所示的是得到的“平滑”纹理(分别是缩放因子 2、 4、 8、 16、 32 和 64——从左到右, 从上到下)。 请注意, 缩放因子现在是一个 double 类型量,因为我们需要小数分量来确定每个纹素的插值灰度值。
double smoothNoise(double x1, double y1, double z1) {
// x1、 y1 和 z1 的小数部分(对于当前纹素,从当前块到下一个块的百分比)
double fractX = x1 - (int) x1;
double fractY = y1 - (int) y1;
double fractZ = z1 - (int) z1;
// 在 X、 Y 和 Z 方向上的相邻像素的索引
int x2 = ((int)x1 + noiseWidth + 1) % noiseWidth;
int y2 = ((int)y1 + noiseHeight + 1) % noiseHeight;
int z2 = ((int)z1 + noiseDepth + 1) % noiseDepth;
// 通过按照 3 个轴方向插值灰度,平滑噪声
double value = 0.0;
// 取原始“块状”噪声图中纹素周围的 8 个灰度值的加权平均值
// 它平均纹素所在的小“块”的 8 个顶点处的颜色值
value += (1-fractX)*(1-fractY)*(1-fractZ)*noise[(int)x1][(int)y1][(int)z1];
value += (1-fractX)*fractY*(1-fractZ)*noise[(int)x1][(int)y2][(int)z1];
value += fractX*(1-fractY)*(1-fractZ)*noise[(int)x2][(int)y1][(int)z1];
value += fractX*fractY*(1-fractZ)*noise[(int)x2][(int)y2][(int)z1];
value += (1-fractX)*(1-fractY)*fractZ *noise[(int)x1][(int)y1][(int)z2];
value += (1-fractX)*fractY*fractZ*noise[(int)x1][(int)y2][(int)z2];
value += fractX*(1-fractY)*fractZ*noise[(int)x2][(int)y1][(int)z2];
value += fractX*fractY *fractZ *noise[(int)x2][(int)y2][(int)z2];
return value;
}
double turbulence(double x, double y, double z, double size) {
double value = 0.0, initialSize = size;
while (size >= 0.9) {
value += smoothNoise(x / size, y / size, z / size) * size;
size /= 2.0;
}
value = 128.0 * value / initialSize;
return value;
}
double logistic(double x) {
double k = 3.0;
return (1.0 / (1.0 + pow(2.718, -k*x)));// 自然常量e=2.7182818284……
}
void fillDataArray(GLubyte data[]) {
double veinFrequency = 1.75;// 调整“块”数量
double turbPower = 3.0;// 缩放系数
double turbSize = 32.0;// 调整“块”中的扰动量
for (int i = 0; i<noiseHeight; i++) {
for (int j = 0; j<noiseWidth; j++) {
for (int k = 0; k<noiseDepth; k++) {
double xyzValue = (float)i / noiseWidth + (float)j / noiseHeight
+ (float)k / noiseDepth + turbPower * turbulence(i, j, k, turbSize) / 256.0;
double sineValue = logistic(abs(sin(xyzValue * 3.14159 * veinFrequency)));
sineValue = max(-1.0, min(sineValue*1.25 - 0.20, 1.0));
float redPortion = 255.0f * (float)sineValue;
float greenPortion = 255.0f * (float)min(sineValue*1.5 - 0.25, 1.0);
float bluePortion = 255.0f * (float)sineValue;
data[i*(noiseWidth*noiseHeight * 4) + j*(noiseHeight * 4) + k * 4 + 0] = (GLubyte)redPortion;
data[i*(noiseWidth*noiseHeight * 4) + j*(noiseHeight * 4) + k * 4 + 1] = (GLubyte)greenPortion;
data[i*(noiseWidth*noiseHeight * 4) + j*(noiseHeight * 4) + k * 4 + 2] = (GLubyte)bluePortion;
data[i*(noiseWidth*noiseHeight * 4) + j*(noiseHeight * 4) + k * 4 + 3] = (GLubyte)255;
}
}
}
}

“logistic”(或“ sigmoid”)函数具有 S 形曲线,两端都有渐近线。常见的例子是 f(x) = 1/(1+e−x) 和 双曲正切函数 tanh(x)=sinh(x)/cosh(x)。它们有时也被称为“挤压”函数。
smoothNoise()函数通过计算相应原始“块状”噪声图中纹素周围的 8 个灰度值的加权平均值来计算给定噪声图的平滑版本中的每个纹素的灰度值。也就是说,它平均纹素所在的小“块”的 8 个顶点处的颜色值。这些“邻居”颜色中的每一个的权重基于纹素与其每个邻居的距离,并归一化到范围[0…1]。
接下来,组合各种缩放因子的平滑噪声图。创建一个新的噪声图,其中每个纹素由另一个加权平均值形成,这次基于每个“平滑”噪声图中相同位置的纹素的总和,其中缩放因子用作权重。这种效应被 Perlin 称为“湍流”,尽管它与通过求和各种波形产生的谐波实际上更为密切相关。 新的 turbulence()函数和 fillDataArray()的修改版本指定了一个噪声图,该图对缩放级别 1~32( 2 的各次幂)进行求和,如下所示。其中还显示了以此产生的噪声图在立方体上贴图的结果。
double turbulence(double x, double y, double z, double maxZoom) {
double sum = 0.0, zoom = maxZoom;
while (zoom >= 1.0) {// 最后一遍是当 zoom = 1 时
// 计算平滑后的噪声图的加权和
sum = sum + smoothNoise(x / zoom, y / zoom, z / zoom) * zoom;
zoom = zoom / 2.0; // 对每个 2 的幂的缩放因子
}
sum = 128.0 * sum / maxZoom; // 对不大于 64 的 maxZoom 值,保证 RGB < 256
return sum;
}
void fillDataArray(GLubyte data[ ] ) {
double maxZoom = 32.0;
for (int i=0; i<noiseWidth; i++) {
for (int j=0; j<noiseHeight; j++) {
for (int k=0; k<noiseDepth; k++) {
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+0] = (GLubyte) turbulence(i, j, k, maxZoom);
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+1] = (GLubyte) turbulence(i, j, k, maxZoom);
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+2] = (GLubyte) turbulence(i, j, k, maxZoom);
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+3] = (GLubyte) 255;
} } } }

噪声应用——大理石
通过修改噪声图并使用适当的 ADS 材料添加 Phong 照明,我们可以使龙模型看起来像一块大理石般的石头。
我们首先生成一个条纹图案,有点类似于本章前面的“条纹”示例——新条纹与之前的条纹不同,首先是因为它们是对角线,还因为它们是由正弦波产生的,因此边缘是模糊的。然后,我们使用噪声图来扰动这些线,将它们存储为灰度值。 fillDataArray()函数的更改如下:
void fillDataArray(GLubyte data[ ]) {
double veinFrequency = 2.0;
double turbPower = 1.5;
double maxZoom = 64.0;
for (int i=0; i<noiseWidth; i++) {
for (int j=0; j<noiseHeight; j++) {
for (int k=0; k<noiseDepth; k++) {
double xyzValue = (float)i / noiseWidth + (float)j / noiseHeight + (float)k / noiseDepth
+ turbPower * turbulence(i,j,k,maxZoom) / 256.0;
double sineValue = abs(sin(xyzValue * 3.14159 * veinFrequency));
float redPortion = 255.0f * (float)sineValue;
float greenPortion = 255.0f * (float)sineValue;
float bluePortion = 255.0f * (float)sineValue;
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+0] = (GLubyte) redPortion;
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+1] = (GLubyte) greenPortion;
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+2] = (GLubyte) bluePortion;
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+3] = (GLubyte) 255;
} } } }
变量 veinFrequency 用于调整条纹数量, turbSize 调整生成湍流时使用的缩放系数,turbPower 调整条纹中的扰动量(设置为 0时,条纹不受干扰)。由于相同的正弦波值用于所有 3 个( RGB) 颜色分量, 所以存储在图像数据阵列中的最终颜色是灰度级的。下图显示了各种 turbPower 值( 0.0、 5.5、 1.0 和 1.5,从左到右)的结果纹理贴图。

由于我们希望大理石具有闪亮的外观,我们采用 Phong 着色使得“大理石”纹理物体看起来令人信服。前述程序总结了生成大理石龙的代码。除了我们还传递了原始顶点坐标以用作 3D 纹理坐标(如前所述),顶点和片段着色器与用于 Phong 着色的相同。片段着色器使用前述代码中描述的技术将噪声结果与光照结果结合。
// 用于 Phong 着色的白光 ADS 设置
...
float globalAmbient[4] = {0.5f, 0.5f, 0.5f, 1.0f};
float lightAmbient[4] = {0.0f, 0.0f, 0.0f, 1.0f};
float lightDiffuse[4] = {1.0f, 1.0f, 1.0f, 1.0f};
float lightSpecular[4] = {1.0f, 1.0f, 1.0f, 1.0f};
float matShi = 75.0f;
void init(GLFWwindow* window) {
. . .
generateNoise();
noiseTexture = load3DTexture(); // 和前述程序一样,负责调用 fillDataArray()
}
void fillDataArray(GLubyte data[]) {
double veinFrequency = 1.75;
double turbPower = 3.0;
double turbSize = 32.0;
// 剩下部分构建大理石噪声图的和之前的一样
. . .
}
// 顶点着色器,和前述一样
// 片段着色器
. . .
void main(void) {
. . .
// 模型顶点取值[-1.5, +1.5],纹理坐标取值[0, 1]
vec4 texColor = texture(s, originalPosition / 3.0 + 0.5);
fragColor = 0.7 * texColor * (globalAmbient + light.ambient + light.diffuse * max(cosTheta,0.0))
+ 0.5 * light.specular * pow(max(cosPhi, 0.0), material.shininess);
}
有多种方法可以模拟不同颜色的大理石(或其他石材)。改变大理石中“矿脉”颜色的一种方法是修改 fillDataArray()函数中 Color 变量的定义,例如,通过增加绿色成分:
float redPortion = 255.0f * (float)sineValue;
float greenPortion = 255.0f * (float)min(sineValue*1.5 - 0.25, 1.0);
float bluePortion = 255.0f * (float)sineValue;
我们还可以引入 ADS 材料值[即在 init()中指定]来模拟完全不同类型的石头,例如“玉石”。
下图显示了 4 个示例,前 3 个使用程序上例所示的设置,第四个示例使用“jade” ADS材料值。

噪声应用——木材
棕色的色调可以通过组合相似数量的红色和绿色、少量蓝色来制作。然后,我们应用具有低“光泽”的 Phong 着色。
我们可以通过修改 fillDataArray()函数来生成环绕我们 3D 纹理贴图中 Z 轴的年轮, 使用三角函数指定与 Z 轴等距的 X 和 Y 值。我们使用正弦波循环重复此过程,根据此正弦波均匀地升高和降低红色和绿色成分,以产生不同的棕色调。变量 sineValue 保持精确的色调,可以通过稍微偏移一个分量或另一个分量来调整(在这种情况下,将红色增加 80,将绿色增加 30)。我们可以通过调整 xyPeriod 的值来创建更多(或更少)的年轮。
void fillDataArray(GLubyte data[ ]) {
double xyPeriod = 40.0;
for (int i=0; i<noiseWidth; i++) {
for (int j=0; j<noiseHeight; j++) {
for (int k=0; k<noiseDepth; k++) {
double xValue = (i - (double)noiseWidth/2.0) / (double)noiseWidth;
double yValue = (j - (double)noiseHeight/2.0) / (double)noiseHeight;
double distanceFromZ = sqrt(xValue * xValue + yValue * yValue)
double sineValue = 128.0 * abs(sin(2.0 * xyPeriod * distanceFromZ * 3.14159));
float redPortion = (float)(80 + (int)sineValue);
float greenPortion = (float)(30 + (int)sineValue);
float bluePortion = 0.0f;
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+0] = (GLubyte) redPortion;
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+1] = (GLubyte) greenPortion;
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+2] = (GLubyte) bluePortion;
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+3] = (GLubyte) 255;
} } } }

上图中的木质年轮环是一个很好的开始, 但它们看起来不太逼真——它们太完美了。为了改善这一点,我们使用噪声图(更具体地说,是湍流)来扰动 distanceFromZ 变量,使得环具有轻微的变化。计算修改如下:
double distanceFromZ =
sqrt(xValue * xValue + yValue * yValue)
+ turbPower * turbulence(i, j, k, maxZoom) / 256.0;
同样,变量 turbPower 调整应用了多少湍流(将其设置为 0.0,产生上图所示的未受干扰的版本),并且 maxZoom 指定缩放值(在此示例中为 32)。下图显示了 turbPower 值 0.05、1.0 和 2.0(从左到右)得到的木材纹理。

我们现在可以将 3D 木材纹理贴图应用于模型。通过对用于纹理坐标的 originalPosition顶点位置应用旋转,可以进一步增强纹理的真实感,这是因为用木头雕刻的大多数物品与年轮的方向不完全对齐。为此,我们向着色器发送一个额外的旋转矩阵,以旋转纹理坐标。我们还添加了 Phong 着色,具有适当的木色 ADS 值和适度的光泽度。下面来创建“木质海豚”:
glm::mat4 texRot;
// 木质材质(棕色)
float matAmbient[4] = {0.5f, 0.35f, 0.15f, 1.0f};
float matDiffuse[4] = {0.5f, 0.35f, 0.15f, 1.0f};
float matSpecular[4] = {0.5f, 0.35f, 0.15f, 1.0f};
float matShi = 15.0f;
void init(GLFWwindow* window) {
. . .
// 旋转应用于纹理坐标——增加额外的木纹变化
texRot = glm::rotate(glm::mat4(1.0f), toRadians(20.0f), glm::vec3(0.0f, 1.0f, 0.0f));
}
void fillDataArray(GLubyte data[ ]) {
double xyPeriod = 40.0;
double turbPower = 0.1;
double maxZoom = 32.0;
for (int i=0; i<noiseWidth; i++) {
for (int j=0; j<noiseHeight; j++) {
for (int k=0; k<noiseDepth; k++) {
double xValue = (i - (double)noiseWidth/2.0) / (double)noiseWidth;
double yValue = (j - (double)noiseHeight/2.0) / (double)noiseHeight;
double distanceFromZ = sqrt(xValue * xValue + yValue * yValue)
+ turbPower * turbulence(i, j, k, maxZoom) / 256.0;
double sineValue = 128.0 * abs(sin(2.0 * xyPeriod * distanceFromZ * Math.PI));
float redPortion = (float)(80 + (int)sineValue);
float greenPortion = (float)(30 + (int)sineValue);
float bluePortion = 0.0f;
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+0] = (GLubyte) redPortion;
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+1] = (GLubyte) greenPortion;
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+2] = (GLubyte) bluePortion;
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+3] = (GLubyte) 255;
} } } }
void display(GLFWwindow* window, double currentTime) {
. . .
tLoc = glGetUniformLocation(renderingProgram, "texRot");
glUniformMatrix4fv(tLoc, 1, false, glm::value_ptr(texRot));
. . .
}
##############################################################
//顶点着色器
. . .
uniform mat4 texRot;
void main(void) {
. . .
/*
顶点位置可能因旋转而移动超出[-1…1]的范围
*/
originalPosition = vec3(texRot * vec4(position,1.0)).xyz;// 绕Y轴旋转20°
gl_Position = proj_matrix * mv_matrix * vec4(position,1.0);
}
//片段着色器
. . .
void main(void) {
. . .
in vec3 originalPosition;// 流经[顶点着色器]后的顶点肯定是规格化了的,即一定处于[-1,1]区间
. . .
// 将光照和 3D 纹理结合
/** 注:如果顶点位置因在顶点着色器中旋转而超出[-1…1]范围,则取样参数就会超出所需的[0…1],
此时要这样处理:将rotatedOriginalPosition除以更大的数字、加上稍大的数字。
例如:假设现在顶点坐标范围为[-1-α,1+β],其中α>0,β>0,除以4.0、加上0.6,则:
原采取参数 = rotatedOriginalPosition/2.0+0.5 ∈[-0.5×α, 1+0.5×β],显然参数范围错误。
现采取参数 = rotatedOriginalPosition/4.0+0.6 ∈[0.35-0.25×α, 0.85+0.25×β]∈[0,1],参数范围正确。
*/
vec4 texColor = texture(s, originalPosition/2.0+0.5);
fragColor = 0.5 * texColor
+ 0.5 * (globalAmbient * matAmb + light.ambient * matAmb
+ light.diffuse * matDiff * max(cosTheta,0.0)
+ light.specular * matSpec * pow(max(cosPhi,0.0), material.shininess)
);
}
实际运行程序,发现最终效果图显示出来的速度比较慢,可能需要十几秒吧。

片段着色器中还有一个值得注意的细节。由于我们在 3D 纹理内旋转模型,所以有时可能会导致顶点位置因旋转而移动超出所需的[0…1]纹理坐标范围。如果发生这种情况,我们可以通过将原始顶点位置除以更大的数字(例如 4.0 而不是 2.0)来调整这种可能性,然后添加稍大一些的数字(例如 0.6)以使其在纹理空间中居中。
二维纹理旋转逻辑如下图,图中标示了顶点与纹理图像的对应关系。
注意:旋转的是从纹理图像上取样点的坐标而不是纹理图像本身。

噪声应用——云
前面构建的“湍流”噪声图看起来有点像云。当然,它不是正确的颜色,所以我们首先将它从灰度变为适当的浅蓝色和白色混合。一种直接的方法是为蓝色分量指定一个最大值为 1.0 的颜色,为红色和绿色分量指定 0.0~1.0 的变化(但相等的)值,具体取决于噪声图中的值。新的 fillDataArray()函数如下:
void fillDataArray(GLubyte data[]) {
for (int i=0; i<noiseWidth; i++) {
for (int j=0; j<noiseHeight; j++) {
for (int k=0; k<noiseDepth; k++) {
float brightness = 1.0f - (float) turbulence(i,j,k,32) / 256.0f;
float redPortion = brightness*255.0f;
float greenPortion = brightness*255.0f;
float bluePortion = 1.0f*255.0f;
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+0] = (GLubyte) redPortion;
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+1] = (GLubyte) greenPortion;
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+2] = (GLubyte) bluePortion;
data[i*(noiseWidth*noiseHeight*4)+j*(noiseHeight*4)+k*4+3] = (GLubyte) 255;
} } } }
生成的蓝色版本的噪声图现在可用于纹理化天幕。 回想一下, 天幕是一个球体或半球体,在禁用深度测试的情况下被纹理化和渲染,并放置使其围绕相机(类似于天空盒)。
构建天幕的一种方法是使用顶点坐标作为纹理坐标,以与我们对其他 3D 纹理相同的方式对其进行纹理化。然而,在这种情况下,事实证明使用天幕的 2D 纹理坐标会产生看起来更像云的图案, 因为球面扭曲会略微拉伸纹理贴图。 我们可以通过将 GLSL 的 texture()调用中的第三维设置为常量值来从噪声图中获取 2D 切片。假设天幕的纹理坐标已经以标准方式发送到顶点属性中的 OpenGL 管线,下面的片段着色器使用噪声图的 2D 切片对其进行纹理化:
// 顶点着色器
layout (location = 1) in vec2 texCoord;
out vec2 tc;
out vec3 originalPosition;
...
originalPosition = position;
tc = texCoord;
...
// 片段着色器
#version 430
in vec2 tc;
out vec4 fragColor;
layout(binding = 0) uniform sampler3D s;// 注:是“3D”采样器变量;C++/OpenGL程序中构建的3D纹理复制到3D纹理单元。
void main() {
fragColor = texture(s, vec3(tc.x, tc.y, 0.5));
}
得到的纹理化天幕如下图所示。虽然相机通常被放置在天幕内,但我们在外面使用相机进行渲染,因此可以看到圆顶本身的效果。当前的噪声图导致云“看起来模糊不清”。

虽然我们的朦胧云看起来不错,但我们希望能够塑造它们——也就是说,让它们更多或更少朦胧。 一种方法是修改 turbulence()函数,使其使用指数(如 logistic 函数), 让云看起来更“明显”。修改后的 turbulence()函数以及相关的 logistic()函数如之前程序所示。完整的程序还包含前面描述的 smooth()、 fillDataArray()和 generateNoise()函数。
double turbulence(double x, double y, double z, double size) {
double value = 0.0, initialSize = size, cloudQuant;
while(size >= 0.9) {
value = value + smoothNoise(x/size, y/size, z/size) * size;
size = size / 2.0;
}
cloudQuant = 110.0; // 可微调的云质量
value = value / initialSize;
value = 256.0 * logistic(value * 128.0 - cloudQuant);
return value;
}
double logistic(double x) {
double k = 0.2; // 可微调的云朦胧程度,产生更多或更少的分明的云边界
return (1.0 / (1.0 + pow(2.718, -k*x)));
}
logistic 函数使颜色更倾向于白色或蓝色, 而不是介于两者之间的值,从而产生具有更多不同云边界的视觉效果。变量 cloudQuant 调整噪声图中白色(相对于蓝色)的相对量,这反过来导致当应用 logistic 函数时产生更多(或更少)的白色区域(即不同的云)。由此产生的天幕现在具有更明显的云层,如下图所示。

为了增强云的真实感,我们应该通过以下方式使它们变得生动:
(a)使它们随着时间的推移而移动或“漂移”;
(b)随着它们漂移逐渐改变它们的形状。
使云“漂移”的一种简单方法是缓慢旋转天幕。这不是一个完美的解决方案,因为真实的云往往会沿着直线方向漂移,而不是围绕观察者旋转。但是,如果旋转缓慢且云只是用于装饰场景,则效果可能是足够的。
随着云的漂移,云逐渐变化,起初可能看起来很棘手。然而,考虑到我们用于纹理云的3D 噪声图,实际上有一种非常简单而聪明的方法来实现这种效果。回想一下,虽然我们为云构建了一个 3D 纹理噪声图,但到目前为止我们只使用了它的一个“切片”,跟天幕的 2D纹理坐标相交(我们将纹理查找的 Z 坐标设置为一个常量值)。到目前为止, 3D 纹理的其余部分尚未使用。
我们的技巧是将纹理查找的常量 Z 坐标替换为随时间逐渐变化的变量。也就是说,当我们旋转天幕时,我们逐渐增加深度变量,导致纹理查找使用不同的切片。回想一下,当我们构建 3D 纹理贴图时,我们将平滑应用于沿 3 个轴的颜色变化。因此,纹理贴图中的相邻切片非常相似,但略有不同。因此,通过逐渐改变 texture()调用中的 Z 值,云的外观将逐渐改变。
double rotAmt = 0.0; // 用来让云看起来漂移的 Y 轴旋转量
float depth = 0.01f; // 3D 噪声图的深度查找,用来使云逐渐变化
. . .
void display(GLFWwindow* window, double currentTime) {
. . .
// 逐渐旋转天幕
mMat = glm::translate(glm::mat4(1.0f), glm::vec3(domeLocX, domeLocY, domeLocZ);
rotAmt += 0.02;
mMat = glm::rotate(mMat, rotAmt, glm::vec3(0.0f, 1.0f, 0.0f));
// 逐渐修改第三个纹理坐标,以使云变化
dLoc = glGetUniformLocation(program, "d");
depth += 0.00005f;
if (depth >= 0.99f)
depth = 0.01f; // 当我们到达纹理贴图的终点时返回开头
glUniform1f(dLoc, depth);
. . .
}
#############################
//片段着色器
#version 430
in vec2 tc;
out vec4 fragColor;
uniform float d;
layout (binding=0) uniform sampler3D s;
void main(void) {
fragColor = texture(s, vec3(tc.x, tc.y, d));// 逐渐改变的"d"替换前面的常量
}
逐渐改变漂移和动画的云的效果如下:

它们从右到左漂移在天幕上,并在漂移时缓慢改变形状。
在 360°点有一条明显的垂直线,可能是程序中以 0.01 而不是 0.0 开始深度变量的原因。但实际测试中发现,就算深度变量初始值设为0.0,一样的有明显的接缝存在。接缝存在的原因很简单,就是任取一个3D噪声纹理的切面,左右和上下两侧的侧边像素颜色不可能刚好能重合。
本示例主要功能完整代码:
HalfSphere.h
class HalfSphere {
private:
int numVertices;
int numIndices;
std::vector<int> indices;
std::vector<glm::vec3> vertices;
std::vector<glm::vec2> texCoords;
std::vector<glm::vec3> normals;
void init(int);
float toRadians(float degrees);
public:
HalfSphere();
HalfSphere(int prec);
int getNumVertices();
int getNumIndices();
std::vector<int> getIndices();
std::vector<glm::vec3> getVertices();
std::vector<glm::vec2> getTexCoords();
std::vector<glm::vec3> getNormals();
};
HalfSphere.cpp
#include "HalfSphere.h"
HalfSphere::HalfSphere() { init(48); }
HalfSphere::HalfSphere(int prec) { init(prec); }
float HalfSphere::toRadians(float degrees) { return (degrees * 2.0f * 3.14159f) / 360.0f; }
void HalfSphere::init(int prec) {
numVertices = (prec + 1) * (prec + 1);
numIndices = prec * prec * 6;
for (int i = 0; i < numVertices; i++) { vertices.push_back(glm::vec3()); }
for (int i = 0; i < numVertices; i++) { texCoords.push_back(glm::vec2()); }
for (int i = 0; i < numVertices; i++) { normals.push_back(glm::vec3()); }
for (int i = 0; i < numIndices; i++) { indices.push_back(0); }
// calculate triangle vertices
for (int i = 0; i <= prec; i++) {
for (int j = 0; j <= prec; j++) {
float y = (float)cos(toRadians(90.0f - i * 90.0f / prec));
float x = -(float)cos(toRadians(j*360.0f / prec))*(float)abs(cos(asin(y)));
float z = (float)sin(toRadians(j*360.0f / (float)(prec)))*(float)abs(cos(asin(y)));
vertices[i*(prec + 1) + j] = glm::vec3(x, y, z);
texCoords[i*(prec + 1) + j] = glm::vec2(((float)j / prec), ((float)i / prec));
normals[i*(prec + 1) + j] = glm::vec3(x, y, z);
}
}
// calculate triangle indices
for (int i = 0; i<prec; i++) {
for (int j = 0; j<prec; j++) {
indices[6 * (i*prec + j) + 0] = i*(prec + 1) + j;
indices[6 * (i*prec + j) + 1] = i*(prec + 1) + j + 1;
indices[6 * (i*prec + j) + 2] = (i + 1)*(prec + 1) + j;
indices[6 * (i*prec + j) + 3] = i*(prec + 1) + j + 1;
indices[6 * (i*prec + j) + 4] = (i + 1)*(prec + 1) + j + 1;
indices[6 * (i*prec + j) + 5] = (i + 1)*(prec + 1) + j;
}
}
}
int HalfSphere::getNumVertices() { return numVertices; }
int HalfSphere::getNumIndices() { return numIndices; }
std::vector<int> HalfSphere::getIndices() { return indices; }
std::vector<glm::vec3> HalfSphere::getVertices() { return vertices; }
std::vector<glm::vec2> HalfSphere::getTexCoords() { return texCoords; }
std::vector<glm::vec3> HalfSphere::getNormals() { return normals; }
main.cpp
#include "HalfSphere.h"
#include "Utils.h"
float toRadians(float degrees) { return (degrees * 2.0f * 3.14159f) / 360.0f; }
#define numVAOs 1
#define numVBOs 3
/* Simulates drifting clouds.
To view the skydome from the inside, move the camera to 0,2,0
and change the winding order to CW.
*/
float cameraX, cameraY, cameraZ;
float objLocX, objLocY, objLocZ;
GLuint renderingProgram;
GLuint vao[numVAOs];
GLuint vbo[numVBOs];
HalfSphere halfSphere(48);
int numSphereVertices;
GLuint skyTexture;
const int noiseHeight = 200;
const int noiseWidth = 200;
const int noiseDepth = 200;
double noise[noiseHeight][noiseWidth][noiseDepth];
// variable allocation for display
GLuint mvLoc, projLoc, dOffsetLoc;
int width, height;
float aspect;
glm::mat4 pMat, vMat, mMat, mvMat;
float rotAmt = 0.0f;
float d = 0.01f; // depth for 3rd dimension of 3D noise texture
// 3D Noise Texture section
double smoothNoise(double x1, double y1, double z1) {
//get fractional part of x, y, and z
double fractX = x1 - (int)x1;
double fractY = y1 - (int)y1;
double fractZ = z1 - (int)z1;
//neighbor values
int x2 = ((int)x1 + noiseWidth + 1) % noiseWidth;
int y2 = ((int)y1 + noiseHeight + 1) % noiseHeight;
int z2 = ((int)z1 + noiseDepth + 1) % noiseDepth;
//smooth the noise by interpolating
double value = 0.0;
value += (1-fractX) * (1-fractY) * (1-fractZ) * noise[(int)x1][(int)y1][(int)z1];
value += (1-fractX) * fractY * (1-fractZ) * noise[(int)x1][(int)y2][(int)z1];
value += fractX * (1-fractY) * (1-fractZ) * noise[(int)x2][(int)y1][(int)z1];
value += fractX * fractY * (1-fractZ) * noise[(int)x2][(int)y2][(int)z1];
value += (1-fractX) * (1-fractY) * fractZ * noise[(int)x1][(int)y1][(int)z2];
value += (1-fractX) * fractY * fractZ * noise[(int)x1][(int)y2][(int)z2];
value += fractX * (1-fractY) * fractZ * noise[(int)x2][(int)y1][(int)z2];
value += fractX * fractY * fractZ * noise[(int)x2][(int)y2][(int)z2];
return value;
}
double logistic(double x) {
double k = 0.2; // tunable haziness of clouds
return (1.0 / (1.0 + pow(2.718, -k*x)));
}
double turbulence(double x, double y, double z, double size) {
double value = 0.0, initialSize = size, cloudQuant;
while (size >= 0.9) {
value = value + smoothNoise(x / size, y / size, z / size) * size;
size = size / 2.0;
}
cloudQuant = 110.0; // tunable quantity of clouds
value = value / initialSize;
value = 256.0 * logistic(value * 128.0 - cloudQuant);
//value = 128.0 * value / initialSize;
return value;
}
void fillDataArray(GLubyte data[]) {
for (int i = 0; i<noiseHeight; i++) {
for (int j = 0; j<noiseWidth; j++) {
for (int k = 0; k<noiseDepth; k++) {
float brightness = 1.0f - (float)turbulence(i, j, k, 32) / 256.0f;
float redPortion = brightness*255.0f;
float greenPortion = brightness*255.0f;
float bluePortion = 1.0f*255.0f;
data[i*(noiseWidth*noiseHeight * 4) + j*(noiseHeight * 4) + k * 4 + 0] = (GLubyte)redPortion;
data[i*(noiseWidth*noiseHeight * 4) + j*(noiseHeight * 4) + k * 4 + 1] = (GLubyte)greenPortion;
data[i*(noiseWidth*noiseHeight * 4) + j*(noiseHeight * 4) + k * 4 + 2] = (GLubyte)bluePortion;
data[i*(noiseWidth*noiseHeight * 4) + j*(noiseHeight * 4) + k * 4 + 3] = (GLubyte)0;
}
}
}
}
GLuint buildNoiseTexture() {
GLuint textureID;
GLubyte* data = new GLubyte[noiseHeight*noiseWidth*noiseDepth * 4];
fillDataArray(data);
glGenTextures(1, &textureID);
glBindTexture(GL_TEXTURE_3D, textureID);
glTexParameteri(GL_TEXTURE_3D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexStorage3D(GL_TEXTURE_3D, 1, GL_RGBA8, noiseWidth, noiseHeight, noiseDepth);
glTexSubImage3D(GL_TEXTURE_3D, 0, 0, 0, 0, noiseWidth, noiseHeight, noiseDepth, GL_RGBA, GL_UNSIGNED_INT_8_8_8_8_REV, data);
return textureID;
}
void generateNoise() {
for (int x = 0; x<noiseHeight; x++) {
for (int y = 0; y<noiseWidth; y++) {
for (int z = 0; z<noiseDepth; z++) {
noise[x][y][z] = (double)rand() / (RAND_MAX + 1.0);
}
}
}
}
// model section
void setupVertices(void) {
std::vector<int> ind = halfSphere.getIndices();
std::vector<glm::vec3> vert = halfSphere.getVertices();
std::vector<glm::vec2> tex = halfSphere.getTexCoords();
std::vector<glm::vec3> norm = halfSphere.getNormals();
numSphereVertices = halfSphere.getNumIndices();
std::vector<float> pvalues;
std::vector<float> tvalues;
std::vector<float> nvalues;
for (int i = 0; i < halfSphere.getNumIndices(); i++) {
pvalues.push_back((vert[ind[i]]).x);
pvalues.push_back((vert[ind[i]]).y);
pvalues.push_back((vert[ind[i]]).z);
tvalues.push_back((tex[ind[i]]).x);
tvalues.push_back((tex[ind[i]]).y);
nvalues.push_back((norm[ind[i]]).x);
nvalues.push_back((norm[ind[i]]).y);
nvalues.push_back((norm[ind[i]]).z);
}
glGenVertexArrays(1, vao);
glBindVertexArray(vao[0]);
glGenBuffers(numVBOs, vbo);
glBindBuffer(GL_ARRAY_BUFFER, vbo[0]);
glBufferData(GL_ARRAY_BUFFER, pvalues.size() * 4, &pvalues[0], GL_STATIC_DRAW);
glBindBuffer(GL_ARRAY_BUFFER, vbo[1]);
glBufferData(GL_ARRAY_BUFFER, tvalues.size() * 4, &tvalues[0], GL_STATIC_DRAW);
glBindBuffer(GL_ARRAY_BUFFER, vbo[2]);// 本例未使用之
glBufferData(GL_ARRAY_BUFFER, nvalues.size() * 4, &nvalues[0], GL_STATIC_DRAW);
}
void init(GLFWwindow* window) {
renderingProgram = Utils::createShaderProgram("vertShader.glsl", "fragShader.glsl");
cameraX = 0.0f; cameraY = 2.0f; cameraZ = 10.0f;
objLocX = 0.0f; objLocY = 0.0f; objLocZ = 0.0f;
glfwGetFramebufferSize(window, &width, &height);
aspect = (float)width / (float)height;
pMat = glm::perspective(1.0472f, aspect, 0.1f, 1000.0f);
setupVertices();
generateNoise();
skyTexture = buildNoiseTexture();
}
void display(GLFWwindow* window, double currentTime) {
glClear(GL_DEPTH_BUFFER_BIT);
glClearColor(1.0, 1.0, 1.0, 1.0);
glClear(GL_COLOR_BUFFER_BIT);
glUseProgram(renderingProgram);
mvLoc = glGetUniformLocation(renderingProgram, "mv_matrix");
projLoc = glGetUniformLocation(renderingProgram, "proj_matrix");
dOffsetLoc = glGetUniformLocation(renderingProgram, "d");
vMat = glm::translate(glm::mat4(1.0f), glm::vec3(-cameraX, -cameraY, -cameraZ));
mMat = glm::translate(glm::mat4(1.0f), glm::vec3(objLocX, objLocY, objLocZ));
mMat = glm::scale(glm::mat4(1.0f), glm::vec3(4.0f, 4.0f, 4.0f));
rotAmt += 0.002f;
mMat = glm::rotate(mMat, rotAmt, glm::vec3(0.0f, 1.0f, 0.0f));
mvMat = vMat * mMat;
d += 0.00005f; if (d >= 0.99f) d = 0.01f;
glUniformMatrix4fv(mvLoc, 1, GL_FALSE, glm::value_ptr(mvMat));
glUniformMatrix4fv(projLoc, 1, GL_FALSE, glm::value_ptr(pMat));
glUniform1f(dOffsetLoc, d);
glBindBuffer(GL_ARRAY_BUFFER, vbo[0]);
glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 0, 0);
glEnableVertexAttribArray(0);
glBindBuffer(GL_ARRAY_BUFFER, vbo[1]);
glVertexAttribPointer(1, 2, GL_FLOAT, GL_FALSE, 0, 0);
glEnableVertexAttribArray(1);
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_3D, skyTexture);
glEnable(GL_CULL_FACE);
glFrontFace(GL_CCW);
glEnable(GL_DEPTH_TEST);
glDepthFunc(GL_LEQUAL);
glDrawArrays(GL_TRIANGLES, 0, numSphereVertices);
}
int main(void) {
...
}
vertShader.glsl
#version 430
layout (location = 0) in vec3 position;
layout (location = 1) in vec2 texCoord;
out vec2 tc;
uniform mat4 mv_matrix;
uniform mat4 proj_matrix;
void main(void){
tc = texCoord;
gl_Position = proj_matrix * mv_matrix * vec4(position, 1.0);
}
fragShader.glsl
#version 430
in vec2 tc;
out vec4 fragColor;
uniform float d;
layout (binding = 0) uniform sampler3D s;
void main(void) {
fragColor = texture(s, vec3(tc.x, tc.y, d));
}
噪声应用——特殊效果

void display() {
...
tLoc = glGetUniformLocation(renderingProgram, "t");
threshold += 0.002f;
glUniform1f(tLoc, threshold);
...
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_3D, noiseTexture);
glActiveTexture(GL_TEXTURE1);
glBindTexture(GL_TEXTURE_2D, earthTexture);
...
glDrawArrays(GL_TRIANGLES, 0, numSphereVertices);
// 顶点着色器
#version 430
layout (location = 0) in vec3 position;
layout (location = 1) in vec2 tex_coord;
out vec2 tc;
out vec3 originalPosition;
uniform mat4 mv_matrix;
uniform mat4 proj_matrix;
void main(void) {
originalPosition = position;
tc = tex_coord;
gl_Position = proj_matrix * mv_matrix * vec4(position,1.0);
}
// 片段着色器
#version 430
in vec2 tc;// 从地球纹理中取样的2维纹理坐标
in vec3 originalPosition;// 从噪声纹理中取样的3维纹理坐标
out vec4 fragColor;
uniform float t;
layout(binding = 0) uniform sampler3D noiseSampler;
layout(binding = 1) uniform sampler2D earthSampler;
void main() {
float noise = texture(noiseSampler, originalPosition/2.0+0.5).x;// 获取噪声3D纹素RGBA的R分量∈[0,1]
if (noise > t) {// 如果噪声值大于当前阈值
fragColor = texture(earthSampler, tc);// 则使用地球纹理渲染片段
} else {// 否则丢弃片段(不要渲染)
discard;// 这是一个GLSL命令
}
}
为了促进溶解效果,我们引入了 GLSL 的 discard 命令。此命令仅在片段着色器中是合法的,并且在执行时,它会导致片段着色器丢弃当前片段(意味着不渲染它)。
我们的策略很简单。在 C++/OpenGL 应用程序中,我们创建了一个细粒度噪声纹理贴图,以及随时间逐渐增加的浮点变量计数器。然后,此变量在着色器管线中以统一变量发送,并且噪声图也放置在具有关联采样器的纹理贴图中。然后片段着色器使用采样器访问噪声纹理——在这种情况下, 我们使用返回的噪声值来确定是否丢弃该片段。我们通过将灰度噪声值与计数器进行比较来实现这一点,计数器用作一种“阈值”值。因为阈值随着时间的推移逐渐变化,我们可以将其设置为逐渐丢弃越来越多的片段。结果是物体似乎逐渐溶解。
如果可能,丢弃命令应该谨慎使用,因为它可能会导致性能损失。这是因为它的存在使 OpenGL 更难以优化 Z 缓冲深度测试。
GLSL noise()系列函数:
float noise1(genType x);
vec2 noise2(genType x);
vec3 noise3(genType x);
vec4 noise4(genType x);
使用伪随机噪声函数生成值。
x - 指定用于设定噪波函数种子的值。
noise1、noise2、noise3和noise4基于输入值x返回噪声值(矢量或标量)。
噪声函数是一个随机函数,可以用来增加视觉复杂度。噪波函数返回的值看起来是随机的,但不是真正随机的。它们被定义为具有以下特征:
- 返回值始终在[-1.0,1.0]范围内,并且至少覆盖了[-0.6,0.6]范围,具有高斯分布。
- 返回值的总体平均值为0.0。
- 它们是可重复的,因为特定的输入值总是会产生相同的返回值。
- 它们在旋转下具有统计不变性(即,无论域如何旋转,它都具有相同的统计特征)。
- 它们在平移下具有统计不变性(即,无论域如何平移,它都具有相同的统计特征)。
- 在翻译时,它们通常给出不同的结果。
- 空间频率非常集中,集中在0.5到1.0之间。
- 它们在任何地方都是C1连续的(即一阶导数是连续的)。
补充说明
本章生成的噪声图基于 Lode Vandevenne描述的程序。我们的 3D 云生成仍存在一些不足之处。纹理不是无缝的,所以在 360°点有一条明显的垂直线(这也是我们在程序中以 0.01 而不是 0.0 开始深度变量的原因,以避免在噪声图的 Z 维中遇到接缝)。如果需要,也有用于去除接缝的简单方法。另一个问题是在天幕的北峰处,天幕中的球形畸变会产生枕形效应。
我们在本章中实现的云也无法模拟真实云的一些重要方面,例如它们散射太阳光的方式。真正的云也往往在顶部更白,在底部更灰暗。我们的云也没有达到许多实际云所具有的 3D“蓬松”外观。类似地,存在用于产生雾的更全面的模型,例如 Kilgard 和 Fernando描述的模型。
在阅读 OpenGL 文档时,读者可能会注意到 GLSL 包含一些名为 noise1()、 noise2()、noise3()和 noise4()的噪声函数,它们被描述为采用输入种子并产生类似高斯的随机输出。我们在本章中没有使用这些函数,因为在撰写本文时,大多数供应商都没有实现它们。例如,无论输入种子如何,许多 NVIDIA 显卡目前只会为这些函数返回 0 值。





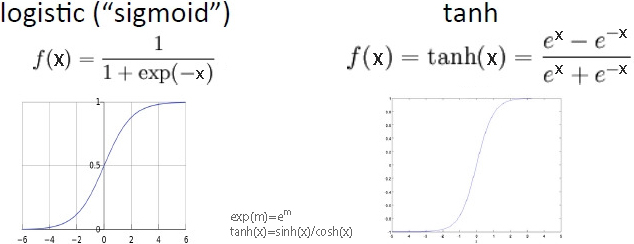

















 279
279

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










