kalman 滤波

卡尔曼滤波分成两步：观测更新 + 运动预测

观测更新

先验分布的均值、方差分别为$\mu ,\sigma$
观测分布的均值、方差分别为$\nu ,\gamma$

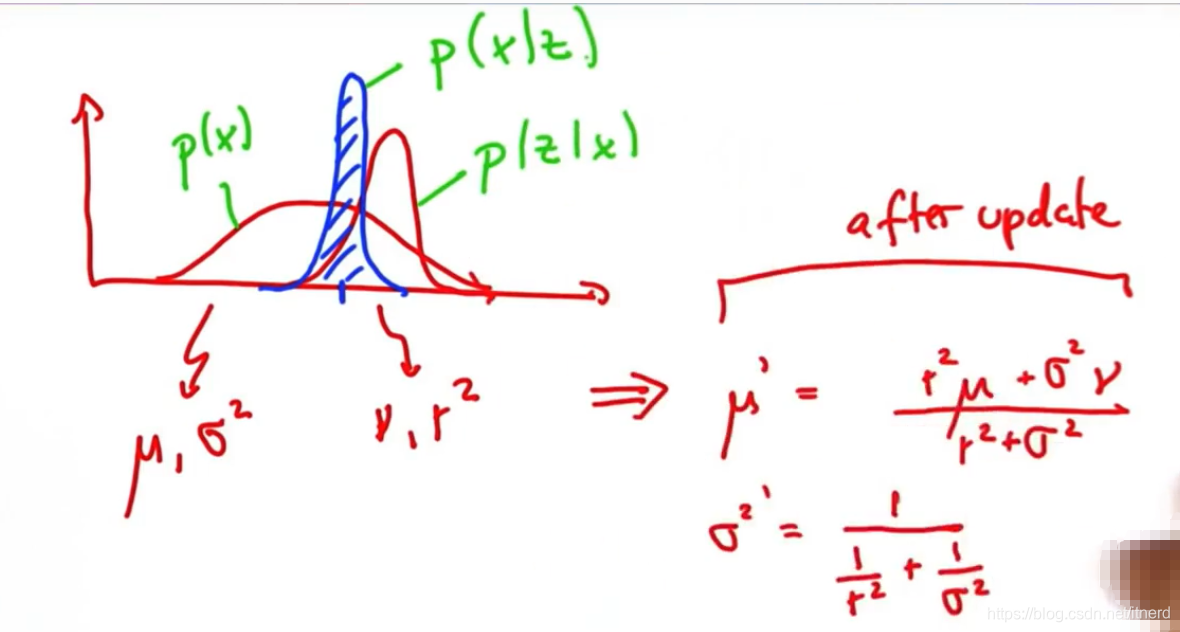
后验分布的均值介于 $\mu ,\nu$之间，方差却比前两者要小。

运动更新(预测)

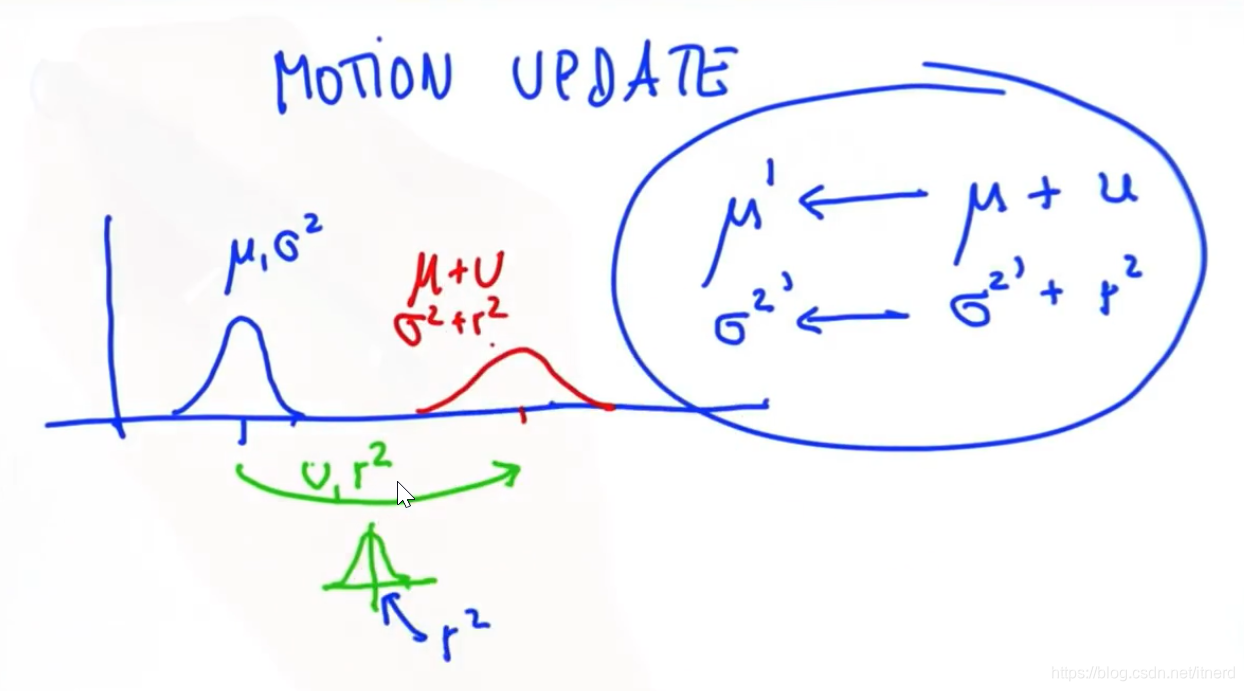
两个高斯分布相加（当前位置+位移量）：均值相加，方差相加

矩阵形式的 kalman 滤波方程

自定义矩阵类

# Write a function 'kalman_filter' that implements a multi-
# dimensional Kalman Filter for the example given

from math import *


class matrix:
    
    # implements basic operations of a matrix class
    
    def __init__(self, value):
        self.value = value
        self.dimx = len(value)
        self.dimy = len(value[0])
        if value == [[]]:
            self.dimx = 0
    
    def zero(self, dimx, dimy):
        # check if valid dimensions
        if dimx < 1 or dimy < 1:
            raise ValueError, "Invalid size of matrix"
        else:
            self.dimx = dimx
            self.dimy = dimy
            self.value = [[0 for row in range(dimy)] for col in range(dimx)]
    
    def identity(self, dim):
        # check if valid dimension
        if dim < 1:
            raise ValueError, "Invalid size of matrix"
        else:
            self.dimx = dim
            self.dimy = dim
            self.value = [[0 for row in range(dim)] for col in range(dim)]
            for i in range(dim):
                self.value[i][i] = 1
    
    def show(self):
        for i in range(self.dimx):
            print(self.value[i])
        print(' ')
    
    def __add__(self, other):
        # check if correct dimensions
        if self.dimx != other.dimx or self.dimy != other.dimy:
            raise ValueError, "Matrices must be of equal dimensions to add"
        else:
            # add if correct dimensions
            res = matrix([[]])
            res.zero(self.dimx, self.dimy)
            for i in range(self.dimx):
                for j in range(self.dimy):
                    res.value[i][j] = self.value[i][j] + other.value[i][j]
            return res
    
    def __sub__(self, other):
        # check if correct dimensions
        if self.dimx != other.dimx or self.dimy != other.dimy:
            raise ValueError, "Matrices must be of equal dimensions to subtract"
        else:
            # subtract if correct dimensions
            res = matrix([[]])
            res.zero(self.dimx, self.dimy)
            for i in range(self.dimx):
                for j in range(self.dimy):
                    res.value[i][j] = self.value[i][j] - other.value[i][j]
            return res
    
    def __mul__(self, other):
        # check if correct dimensions
        if self.dimy != other.dimx:
            raise ValueError, "Matrices must be m*n and n*p to multiply"
        else:
            # multiply if correct dimensions
            res = matrix([[]])
            res.zero(self.dimx, other.dimy)
            for i in range(self.dimx):
                for j in range(other.dimy):
                    for k in range(self.dimy):
                        res.value[i][j] += self.value[i][k] * other.value[k][j]
            return res
    
    def transpose(self):
        # compute transpose
        res = matrix([[]])
        res.zero(self.dimy, self.dimx)
        for i in range(self.dimx):
            for j in range(self.dimy):
                res.value[j][i] = self.value[i][j]
        return res
    
    # Thanks to Ernesto P. Adorio for use of Cholesky and CholeskyInverse functions
    
    def Cholesky(self, ztol=1.0e-5):
        # Computes the upper triangular Cholesky factorization of
        # a positive definite matrix.
        res = matrix([[]])
        res.zero(self.dimx, self.dimx)
        
        for i in range(self.dimx):
            S = sum([(res.value[k][i])**2 for k in range(i)])
            d = self.value[i][i] - S
            if abs(d) < ztol:
                res.value[i][i] = 0.0
            else:
                if d < 0.0:
                    raise ValueError, "Matrix not positive-definite"
                res.value[i][i] = sqrt(d)
            for j in range(i+1, self.dimx):
                S = sum([res.value[k][i] * res.value[k][j] for k in range(self.dimx)])
                if abs(S) < ztol:
                    S = 0.0
                try:
                   res.value[i][j] = (self.value[i][j] - S)/res.value[i][i]
                except:
                   raise ValueError, "Zero diagonal"
        return res
    
    def CholeskyInverse(self):
        # Computes inverse of matrix given its Cholesky upper Triangular
        # decomposition of matrix.
        res = matrix([[]])
        res.zero(self.dimx, self.dimx)
        
        # Backward step for inverse.
        for j in reversed(range(self.dimx)):
            tjj = self.value[j][j]
            S = sum([self.value[j][k]*res.value[j][k] for k in range(j+1, self.dimx)])
            res.value[j][j] = 1.0/tjj**2 - S/tjj
            for i in reversed(range(j)):
                res.value[j][i] = res.value[i][j] = -sum([self.value[i][k]*res.value[k][j] for k in range(i+1, self.dimx)])/self.value[i][i]
        return res
    
    def inverse(self):
        aux = self.Cholesky()
        res = aux.CholeskyInverse()
        return res
    
    def __repr__(self):
        return repr(self.value)

一维情形

# Implement the filter function below

def kalman_filter(x, P):
    for n in range(len(measurements)):
        
        # measurement update
        z = matrix([[measurements[n]]])
        y = z - H*x
        S = H*P*H.transpose() + R
        K = P*H.transpose()*S.inverse()
        x = x + K*y
        P = (I-K*H)*P

        # prediction
        x = F*x + u
        P = F*P*F.transpose()
        
    return x,P

############################################
### use the code below to test your filter!
############################################

measurements = [1, 2, 3]

x = matrix([[0.], [0.]]) # initial state (location and velocity)
P = matrix([[1000., 0.], [0., 1000.]]) # initial uncertainty
u = matrix([[0.], [0.]]) # external motion
F = matrix([[1., 1.], [0, 1.]]) # next state function
H = matrix([[1., 0.]]) # measurement function
R = matrix([[1.]]) # measurement uncertainty
I = matrix([[1., 0.], [0., 1.]]) # identity matrix

print(kalman_filter(x, P))
# output should be:
# x: [[3.9996664447958645], [0.9999998335552873]]
# P: [[2.3318904241194827, 0.9991676099921091], [0.9991676099921067, 0.49950058263974184]]

二维情形

########################################

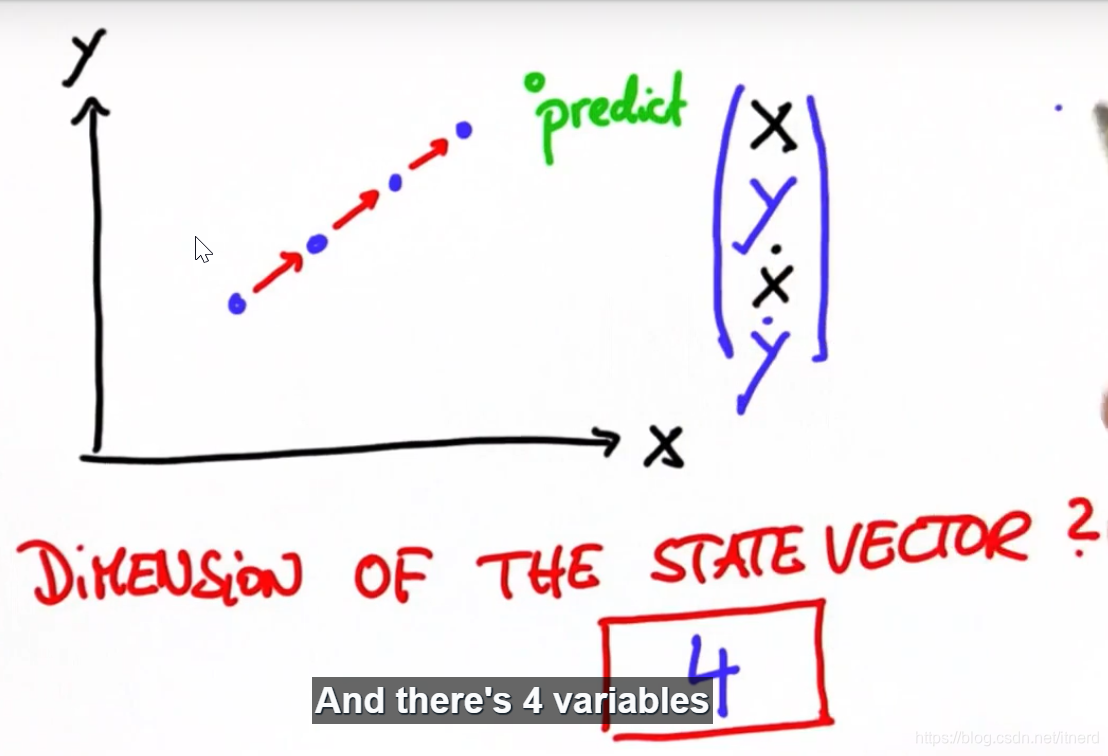
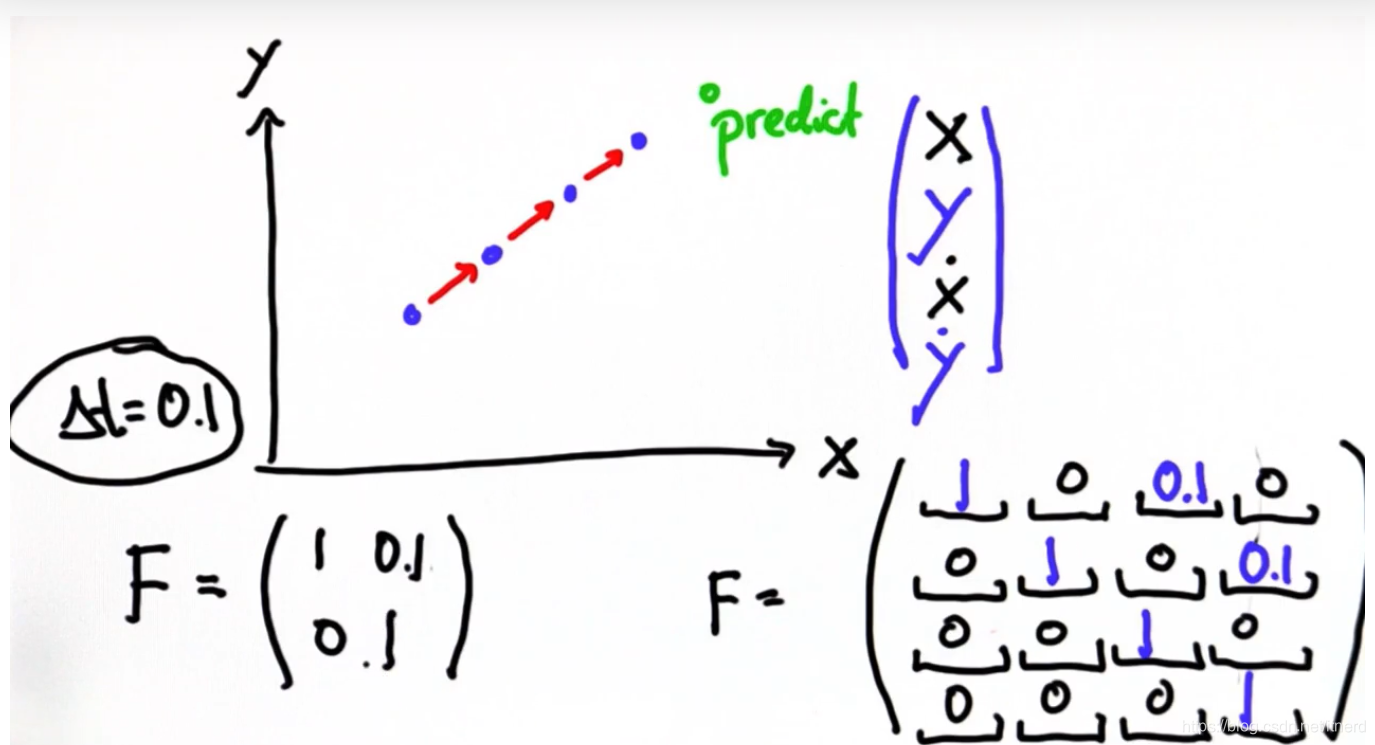
def filter(x, P):
    for n in range(len(measurements)):
        
        # prediction
        x = (F * x) + u
        P = F * P * F.transpose()
        
        # measurement update
        Z = matrix([measurements[n]])
        y = Z.transpose() - (H * x)
        S = H * P * H.transpose() + R
        K = P * H.transpose() * S.inverse()
        x = x + (K * y)
        P = (I - (K * H)) * P
    
    print 'x= '
    x.show()
    print 'P= '
    P.show()

########################################

print "### 4-dimensional example ###"

measurements = [[5., 10.], [6., 8.], [7., 6.], [8., 4.], [9., 2.], [10., 0.]]
initial_xy = [4., 12.]

# measurements = [[1., 4.], [6., 0.], [11., -4.], [16., -8.]]
# initial_xy = [-4., 8.]

# measurements = [[1., 17.], [1., 15.], [1., 13.], [1., 11.]]
# initial_xy = [1., 19.]

dt = 0.1

x = matrix([[initial_xy[0]], [initial_xy[1]], [0.], [0.]]) # initial state (location and velocity)
u = matrix([[0.], [0.], [0.], [0.]]) # external motion

#### DO NOT MODIFY ANYTHING ABOVE HERE ####
#### fill this in, remember to use the matrix() function!: ####

P =  matrix([[0,0,0,0],[0,0,0,0],[0,0,1000,0],[0,0,0,1000]])# initial uncertainty: 0 for positions x and y, 1000 for the two velocities
F =  matrix([[1,0,0.1,0],[0,1,0,0.1],[0,0,1,0],[0,0,0,1]])# next state function: generalize the 2d version to 4d
H =  matrix([[1,0,0,0],[0,1,0,0]])# measurement function: reflect the fact that we observe x and y but not the two velocities
R =  matrix([[0.1,0.],[0.,0.1]])# measurement uncertainty: use 2x2 matrix with 0.1 as main diagonal
I =  matrix([[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]])# 4d identity matrix

###### DO NOT MODIFY ANYTHING HERE #######

filter(x, P)