python 小世界网络

最新推荐文章于 2024-08-27 15:10:37 发布

原创最新推荐文章于 2024-08-27 15:10:37 发布 · 3.3k 阅读

36 ·

CC 4.0 BY-SA版权

我们不生产知识，我们只是互联网的搬运工

文章标签：

#小世界 #python #网络 #可视化

数据可视化同时被 2 个专栏收录

46 篇文章

订阅专栏

复杂网络

22 篇文章

订阅专栏

博客介绍了小世界网络的三个参数：节点数 N、初始节点度 d、断边重连率 α。先依据 N 和 d 构造规则网络，再进行断边重连，不同的断边重连率会使网络呈现不同状态，当重连率为 1 时与 ER 随机网络等价，还提及了网络可视化代码。

部署运行你感兴趣的模型镜像

小世界网络的参数有三个：节点数 $N$ 、初始节点度 $d$ 、断边重连率 $α\alpha$

先根据节点数 $N$ 和初始节点度 $d$ 来构造一个规则网络，网络每个节点的度都是 $d$

A = np.zeros((N, N))
for i in range(N):                          
    t = 0
    while t < (d/2):
        A[i][i-(t+1)] = 1
        A[i-(t+1)][i] = 1
        t += 1

看看网络邻接矩阵 A 的结构，白色表示连边：（ $N = 20, d = 4$ ）
在这里插入图片描述

然后来进行 $断边重连\color{red}断边重连$

for i in range(N):                          
    t = 0
    while t < (N/2):
        if A[i][i-(t+1)] == 1:
            if random.random() < a:
            	# 断边
                A[i][i-(t+1)] = 0
                A[i-(t+1)][i] = 0
                # 重连
                target = random.randint(0,(N-1))
                while A[i][target] == 1 or target == i:
                    target = random.randint(0,(N-1))
                A[i][target] = 1
                A[target][i] = 1
        t += 1

$α=0.2,20%\alpha=0.2, 20\%$ 的边重新连接，总边数为： $(N×d)/2=40(N\times d)/2 = 40$ ，断边重连数 $≃40×0.2=8\simeq 40\times 0.2 = 8$

在这里插入图片描述

$α=0.4,40%\alpha=0.4, 40\%$ 的边重新连接
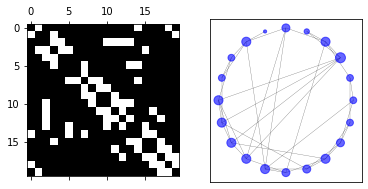
在这里插入图片描述

$α=0.6,60%\alpha=0.6, 60\%$ 的边重新连接
在这里插入图片描述

$α=0.8,80%\alpha=0.8, 80\%$ 的边重新连接

在这里插入图片描述

$α=1\alpha= 1$ ， $100%100\%$ 的边重新连接，此时的小世界网络和 ER随机网络等价。
在这里插入图片描述

网络可视化代码

def small_world(N, d, a):
    A = np.zeros((N, N))
    for i in range(N):                          
        t = 0
        while t < (d/2):
            A[i][i-(t+1)] = 1
            A[i-(t+1)][i] = 1
            t += 1

    for i in range(N):  
        t = 0
        while t < (N/2):
            if A[i][i-(t+1)] == 1:        
                if random.random() < a:         
                    A[i][i-(t+1)] = 0                   
                    A[i-(t+1)][i] = 0
                    target = random.randint(0,(N-1))
                    while A[i][target] == 1 or target == i: 
                        target = random.randint(0,(N-1))
                    A[i][target] = 1                    
                    A[target][i] = 1
            t += 1
    return A                                     

def plot_graph(A, axis=None):
    g = nx.from_numpy_matrix(A)
#     pos  = nx.kamada_kawai_layout(g)
    pos  = nx.circular_layout(g)
    nodesize = []
    maxsize = 100
    minsize = 10
    maxdegree = np.max(np.sum(A,axis=0))
    mindegree = np.min(np.sum(A,axis=0))
    if maxdegree == mindegree:
        nodesize = [maxsize for i in range(len(A))]
    else:
        for node in g:
            size = (np.sum(A[node]) - mindegree)/(maxdegree-mindegree)*(maxsize-minsize)+minsize               #节点大小(节点度数越大，节点越大)
            nodesize.append(size)

    nx.draw_networkx_nodes(g, pos=pos, with_labels=True, node_color='blue', node_size=nodesize, alpha=0.6, ax=axis)
    nx.draw_networkx_edges(g, pos=pos, with_labels=True, width=0.3, alpha=0.6, ax=axis)

for i in [0,0.2,0.4,0.6,0.8,1]:
    A = small_world(20,4, i)
    fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(6,3))
    ax[0].matshow(A, cmap='gray')
    plot_graph(A, axis=ax[1])
    plt.show()