概率图模型

最新推荐文章于 2023-12-31 22:39:35 发布

原创最新推荐文章于 2023-12-31 22:39:35 发布 · 1.5k 阅读

0 ·

CC 4.0 BY-SA版权

我们不生产知识，我们只是互联网的搬运工

机器学习同时被 2 个专栏收录

136 篇文章

订阅专栏

复杂网络

22 篇文章

订阅专栏

概率论中的一些概念

概率
随机变量
分布
条件概率
链式法则
贝叶斯公式
主观概率：先验概率，后验概率
边际分布
联合分布
独立性
条件独立性

概率推断涉及的三个问题

模型选取——模型是否和问题相适配
模型优化——给定数据集，模型的最优参数是什么
模型应用——给定模型，观测到数据的概率是多少

其中后两点常常迭代进行来优化模型

有向图模型

贝叶斯网络

贝叶斯网络为有向无环图，其节点代表随机变量，边代表依赖关系，每个节点都有一个条件概率分布：
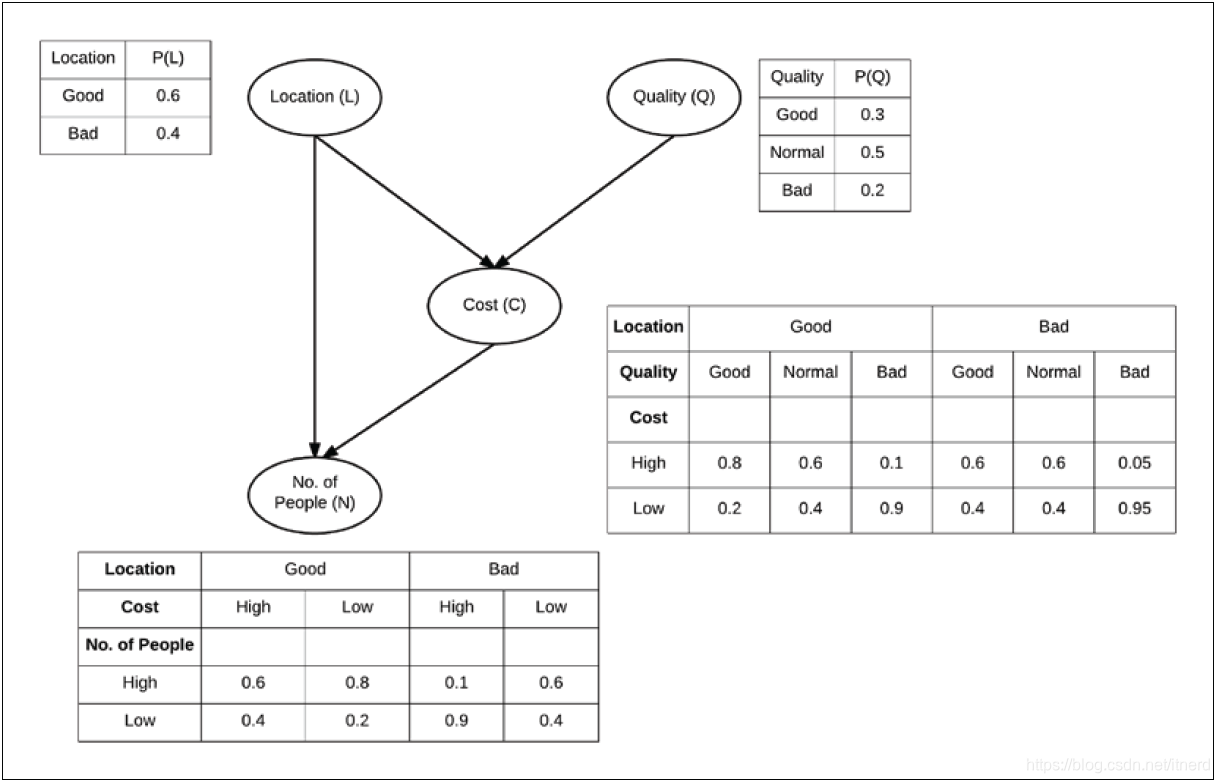
在这里插入图片描述
利用链式法则可以紧致地、模块化地表示概率联合分布：
$P(X_1,X_2,\ldots,X_N) = \Pi_i P(X_i|Par_G(X_i))$ 其中， $Par_G(X)$ 代表 $X$ 在图 $G$ 中的父节点。咱们称上式为联合分布的因子分解。

对于上图，有
$P (Q, C, L, N) = P (Q) P (L) P (C ∣ Q, L) P (N ∣ C, L)$

贝叶斯网络中的推理模式

因果推理
证据推理
混合推理

网络中的概率信息流

贝叶斯网络中变量之间要么是直接连接，要么是间接连接，但总体上可以分为以下四种情况：

因果关系：包含直接、间接因果
证据关系：包含直接、间接证据
同因
同果

判断两个变量是否会影响

能相互影响指的是：以一个变量为条件时，另一个变量的分布会变化，即 $\neq P(X)$

在这里插入图片描述
需要分两种情况讨论：

1. 没有观测量时

除了两个变量同果（ $X\rightarrow W \leftarrow Y$ ），其它情况下两个变量都能相互影响

2. 有观测量时

如果观测量（已知量）出现在因果关系、证据关系的中间环节，则其上游的变量和下游的变量就不能相互影响。要理解也很容易，看看上面的图例就知道，观测变量下游的变量（结点）会受到观测变量的影响，而不可能受到观测变量上游变量的影响，换句话说，观测变量把其上下游变量之间的影响阻断了

相似地，同因关系（ $\leftarrow W \rightarrow Y$ ）中，如果 $W$ 已知，那么 $X, Y$ 也是独立的

同果关系（ $X\rightarrow W \leftarrow Y$ ）则相反，如果 $W$ 未被观测，则 $X, Y$ 是相互独立的。反之，如果 $W$ 或其任一后代节点被观测到，那就意味着 $W$ 的取值已知或者有了某种偏好，那么 $X, Y$ 就不是相互独立了。

对上面的同果关系做进一步说明，同果关系中已知结果 $W$ ，会使不同的原因 $X Y$ 不再独立。
这在生活中是很常见的，举个例子：某天你突然开始鼻塞流涕，这是已知的结果，其原因有很多，你可能认为自己感冒了，或者过敏了，在你不能肯定时，假设它们都有 50%的概率。
然后医生告诉你是感冒了，那么你对过敏性鼻炎的置信度就会大大降低。
也就是说，感冒和过敏两种原因的置信度是相互影响的，当结果已经有了一种确定的解释，另一种可能的原因就不再重要了。

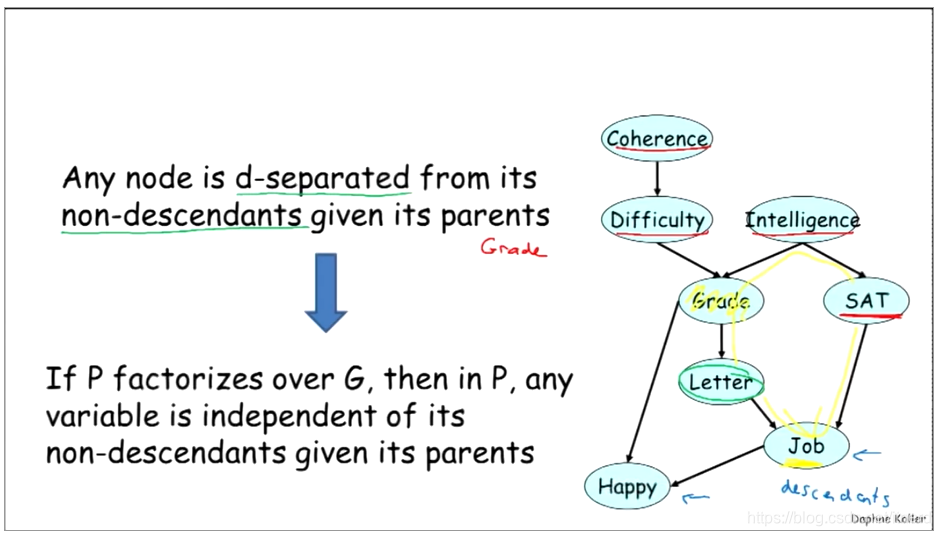
充要条件

在这里插入图片描述

D 分离

X and Y are d-separated in a graph G given a set of observation Z if
there’s no active trail in G between X and Y given Z.

Any node in the graph is d-separated from it’s non-descendants given it’s parents.

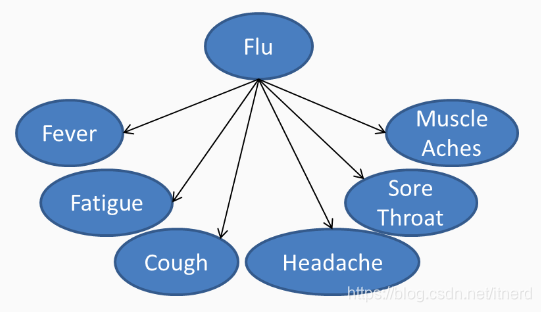
图模型的本质

图模型本质上是用图结构来刻画变量之间的独立性（条件独立性）
在这里插入图片描述

如下图所示的朴素贝叶斯模型，就是一个非常简单的图模型，中心点是类别，它的子结点为特征。该模型描述的条件独立性信息为：给定类别，所有的特征都是独立的，即 $P(X_1, X_2,\ldots,X_n| C) = \Pi_i^n P(X_i|C) \iff X_i \perp X_j | C$
在这里插入图片描述

python 实战

需要安装 python 包：pgmpy

问题描述：一个学生早上开车上学有关的贝叶斯网络，涉及到的关系有

交通事故，大雨 => 交通拥堵
交通拥堵，睡过头了 => 上学迟到
交通拥堵 => 排长队

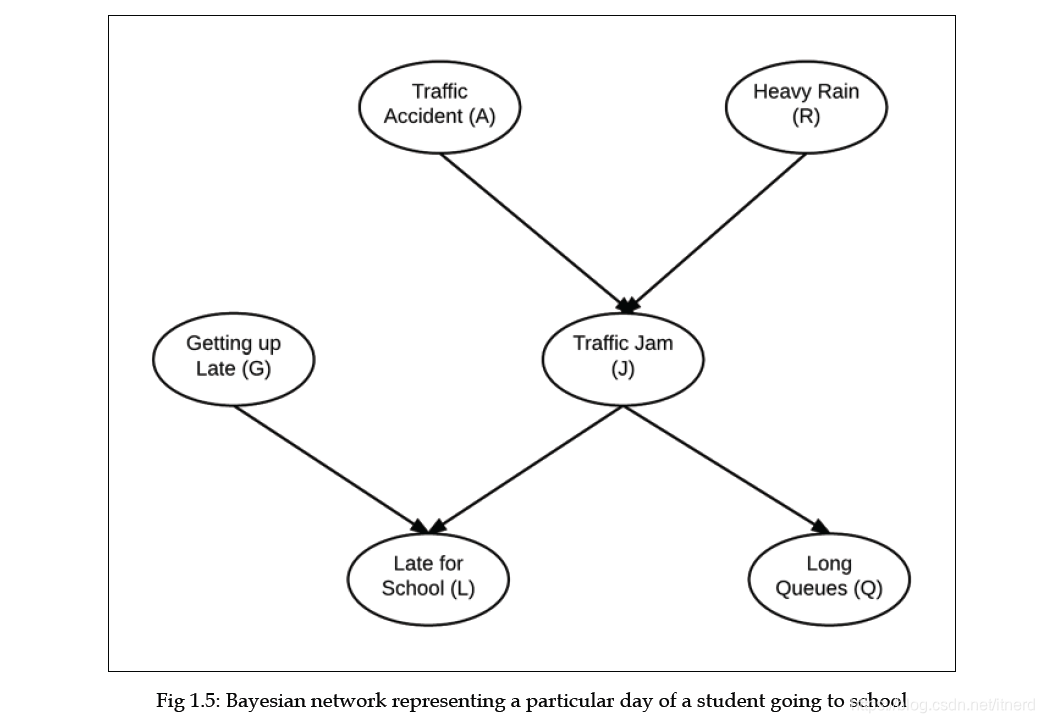
添加结点 A,R,J 及边 A-J,R-J

from pgmpy.models import BayesianModel

model = BayesianModel()
model.add_nodes_from(['rain', 'traffic_jam'])
model.add_edge('rain', 'traffic_jam')
model.add_edge('accident', 'traffic_jam')
print(model.nodes())
'''
['rain', 'traffic_jam', 'accident']
'''
print(model.edges())
'''
[('rain', 'traffic_jam'), ('accident', 'traffic_jam')]
'''

添加结点的条件概率分布(CPD)

from pgmpy.factors.discrete import TabularCPD

cpd_rain = TabularCPD('rain', 2, [[0.4], [0.6]])
cpd_accident = TabularCPD('accident', 2, [[0.2], [0.8]])
cpd_traffic_jam = TabularCPD('traffic_jam',
                             2,
                             [[0.9, 0.6, 0.7, 0.1],
                              [0.1, 0.4, 0.3, 0.9]],
                             evidence=['rain', 'accident'],
                             evidence_card=[2, 2])
model.add_cpds(cpd_rain, cpd_accident, cpd_traffic_jam)

for cpd in model.get_cpds():
    print(cpd)
'''
+---------+-----+
| rain(0) | 0.4 |
+---------+-----+
| rain(1) | 0.6 |
+---------+-----+
+-------------+-----+
| accident(0) | 0.2 |
+-------------+-----+
| accident(1) | 0.8 |
+-------------+-----+
+----------------+-------------+-------------+-------------+-------------+
| rain           | rain(0)     | rain(0)     | rain(1)     | rain(1)     |
+----------------+-------------+-------------+-------------+-------------+
| accident       | accident(0) | accident(1) | accident(0) | accident(1) |
+----------------+-------------+-------------+-------------+-------------+
| traffic_jam(0) | 0.9         | 0.6         | 0.7         | 0.1         |
+----------------+-------------+-------------+-------------+-------------+
| traffic_jam(1) | 0.1         | 0.4         | 0.3         | 0.9         |
+----------------+-------------+-------------+-------------+-------------+
'''

继续扩充模型

添加 Q, J-Q

model.add_node('long_queues')
model.add_edge('traffic_jam', 'long_queues')
cpd_long_queues = TabularCPD('long_queues', 
                             2,
                             [[0.9, 0.2],
                              [0.1, 0.8]],
                             evidence=['traffic_jam'],
                             evidence_card=[2])
model.add_cpds(cpd_long_queues)

添加 G,L, G-L, J-L

model.add_nodes_from(['getting_up_late','late_for_school'])
model.add_edges_from([('getting_up_late', 'late_for_school'),('traffic_jam', 'late_for_school')])
cpd_getting_up_late = TabularCPD('getting_up_late', 2,[[0.6], [0.4]])
cpd_late_for_school = TabularCPD('late_for_school', 
                                 2,
                                 [[0.9, 0.45, 0.8, 0.1],
                                  [0.1, 0.55, 0.2, 0.9]],
                                 evidence=['getting_up_late','traffic_jam'],
                                 evidence_card=[2, 2])
model.add_cpds(cpd_getting_up_late, cpd_late_for_school)

最终模型

model.check_model()  # True

for cpd in model.get_cpds():
    print(cpd)
'''
+---------+-----+
| rain(0) | 0.4 |
+---------+-----+
| rain(1) | 0.6 |
+---------+-----+
+-------------+-----+
| accident(0) | 0.2 |
+-------------+-----+
| accident(1) | 0.8 |
+-------------+-----+
+----------------+-------------+-------------+-------------+-------------+
| rain           | rain(0)     | rain(0)     | rain(1)     | rain(1)     |
+----------------+-------------+-------------+-------------+-------------+
| accident       | accident(0) | accident(1) | accident(0) | accident(1) |
+----------------+-------------+-------------+-------------+-------------+
| traffic_jam(0) | 0.9         | 0.6         | 0.7         | 0.1         |
+----------------+-------------+-------------+-------------+-------------+
| traffic_jam(1) | 0.1         | 0.4         | 0.3         | 0.9         |
+----------------+-------------+-------------+-------------+-------------+
+----------------+----------------+----------------+
| traffic_jam    | traffic_jam(0) | traffic_jam(1) |
+----------------+----------------+----------------+
| long_queues(0) | 0.9            | 0.2            |
+----------------+----------------+----------------+
| long_queues(1) | 0.1            | 0.8            |
+----------------+----------------+----------------+
+--------------------+-----+
| getting_up_late(0) | 0.6 |
+--------------------+-----+
| getting_up_late(1) | 0.4 |
+--------------------+-----+
+--------------------+--------------------+--------------------+--------------------+--------------------+
| getting_up_late    | getting_up_late(0) | getting_up_late(0) | getting_up_late(1) | getting_up_late(1) |
+--------------------+--------------------+--------------------+--------------------+--------------------+
| traffic_jam        | traffic_jam(0)     | traffic_jam(1)     | traffic_jam(0)     | traffic_jam(1)     |
+--------------------+--------------------+--------------------+--------------------+--------------------+
| late_for_school(0) | 0.9                | 0.45               | 0.8                | 0.1                |
+--------------------+--------------------+--------------------+--------------------+--------------------+
| late_for_school(1) | 0.1                | 0.55               | 0.2                | 0.9                |
+--------------------+--------------------+--------------------+--------------------+--------------------+
'''