机器学习之线性回归缩减维度

最新推荐文章于 2025-03-04 17:44:34 发布

原创最新推荐文章于 2025-03-04 17:44:34 发布 · 1.7k 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#lasso #前向逐步回归 #缩减参数 #线性回归

机器学习专栏收录该内容

9 篇文章

订阅专栏

本文深入探讨了高维数据的挑战，特别是维数膨胀带来的问题，并介绍了如何使用Lasso和前向逐步回归法进行数据降维。通过实例解释了在高维空间中样本密度降低的现象，以及这对预测准确性的影响。文章还提供了前向逐步回归法的Python代码实现。

机器学习之线性回归缩减维度

什么叫高维数据？

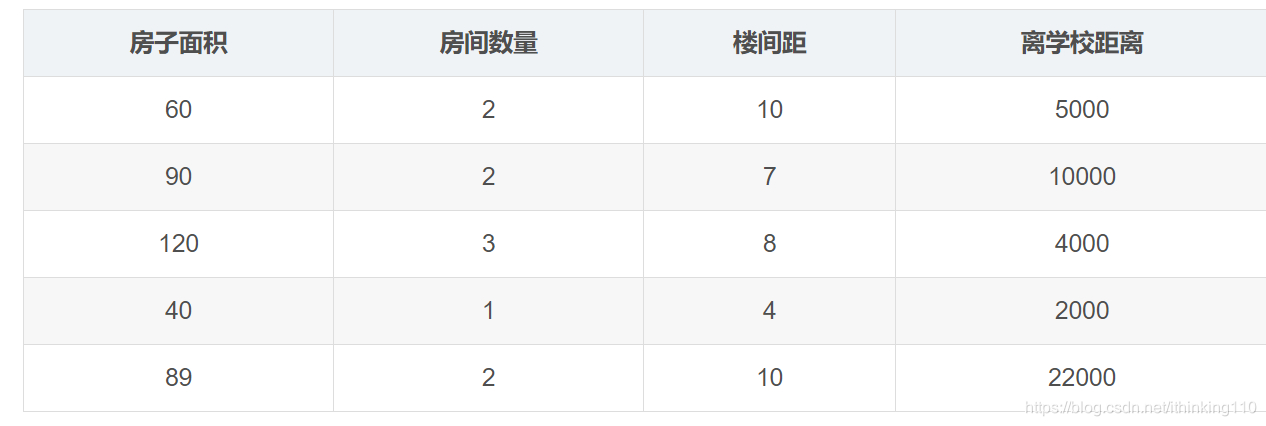
在这里插入图片描述
如上图前面我们求解线性回归的时候列举的一个例子。
这个例子中：
房子的面积，房间的数量，楼间距，离学校的距离我们的数据从这四个维度取例，也称为数据的维度用d表示。
下面的每一行表示一个房子的样本。样本可以有N 多个。

维数膨胀

当我们数据的维度大于样本的数量的时候我们称为维数膨胀

在分析高维数据过程中碰到最大的问题就是维数的膨胀，也就是通常所说的“维数灾难”问题。研究表明，随着维数的增长，分析所需的空间样本数会呈指数增长

如下所示，当数据空间维度由1增加为3，最明显的变化是其所需样本增加；换言之，当样本量确定时，样本密度将会降低，从而样本呈稀疏状态。假设样本量n=12,单个维度宽度为3，那在一维空间下，样本密度为12/3=4，在二维空间下，样本分布空间大小为3*3，则样本密度为12/9=1.33，在三维空间下样本密度为12/27=0.44。
设想一下，当数据空间为更高维时，X=[x1x1,x2x2,….,xnxn]会怎么样？

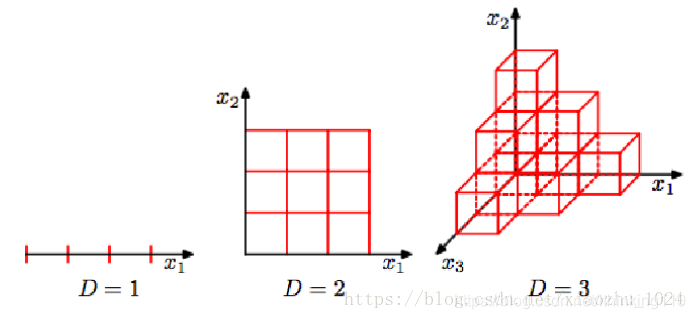
在这里插入图片描述
1,需要更多的样本，样本随着数据维度的增加呈指数型增长；
2,数据变得更稀疏，导致数据灾难；
3,在高维数据空间，预测将变得不再容易；
4, 导致模型过拟合。

数据降维

对于高维数据，维数灾难所带来的过拟合问题，其解决思路是：
1）增加样本量；
2）减少样本特征
而对于现实情况，会存在所能获取到的样本数据量有限的情况，甚至远小于数据维度，即：d>>n。如证券市场交易数据、多媒体图形图像视频数据、航天航空采集数据、生物特征数据等。
常见的降维方法： lasso ，前向逐步回归法,LAR,PCA 等。

这里我们先学习两种 lasso ，前向逐步回归法。

Lasso

这篇文章详细介绍了岭回归
我们得出如下公式：

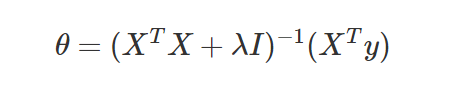
在这里插入图片描述

这个lamda 帮我们解决了不是满秩矩阵的问题。但是其中这个lamda 该取多少值呢？

因为 lamda 这个因子的不确定性所以得到权重也不太一样。

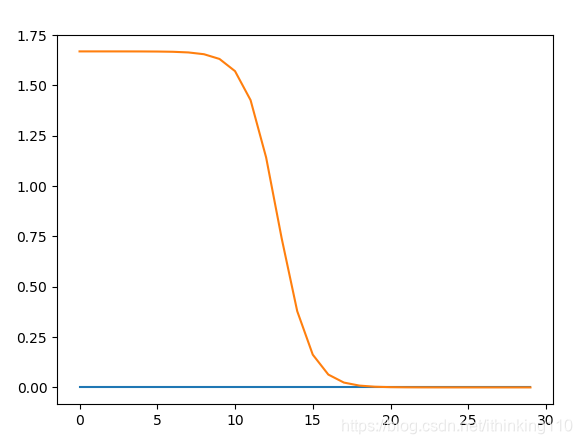
在这里插入图片描述
从这个图中我们可以发现随着 lamda 逐渐变大，权重中的二维权重(x,y) y 值逐渐接近为 0 。
g(z)= w0x0 + 0x1那么我们调节 lamda值就可以减少一个维度的数据。所以岭回归不断可以解决满秩矩阵的问题，还可以缩减维度问题。

lasso 就是对上述的权重和 lamda 在做一个限制。

n
Σ | Wk| ≤ λ
k=1

在λ 足够小的时候，一些系数会因此被迫缩减到 0 。这样就可以减少若干系数。

前向逐步回归法

前向逐步回归法可以得到跟lasso 差不多的效果。但是更加简单。它属于贪心算法。

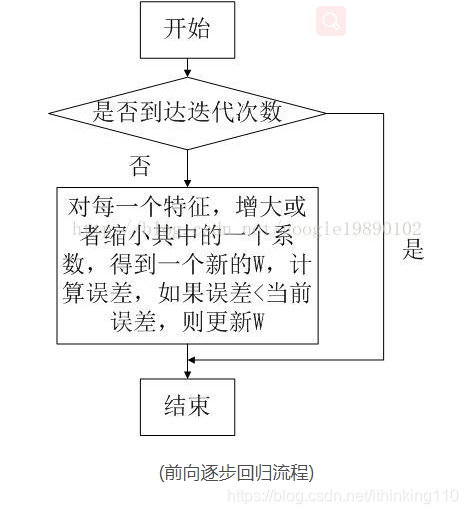
在这里插入图片描述

上图中的增大或者减少这样操作。比如 g(z) = w0* X0 +ｗ1 * X1

让W0 += 0.1 或者 W0 += -0.1 比较哪个误差更小。谁小就取哪个。就跟盲人探路是一回事。盲人没走一步就探测一下前面有坑没有没有就往前走，否则就往后退。

前向逐步回归法代码实现

#coding=utf-8

from  numpy  import *

import  numpy  as np 

import  matplotlib.pyplot  as plt 



filename='./ex1.txt' #文件目录
def loaddataSet(filename):
    numfeat = len(open(filename).readline().split('\t'))-1
    dataMat = [];labelsVec = []
    file = open(filename)
    for line in file.readlines():
        lineArr = []
        curLine = line.strip().split('\t')
        for i in range(numfeat):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelsVec.append(float(curLine[-1]))
    return dataMat,labelsVec
def rssError(yArr,yHatArr): #yArr and yHatArr both need to be arrays
    return ((yArr-yHatArr)**2).sum()
def stageWise(xArr,yArr,eps=0.01,numIt=10):
    xMat = mat(xArr); yMat=mat(yArr).T
    yMean = mean(yMat,0)
    #yMat = yMat - yMean     #can also regularize ys but will get smaller coef
    #xMat = regularize(xMat)
    m,n=shape(xMat)
    returnMat = zeros((numIt,n)) #testing code remove
    ws = zeros((n,1)); wsTest = ws.copy(); wsMax = ws.copy()


    print("wsTest==",wsTest)
    for i in range(numIt):
        print( ws.T)
        lowestError = inf; 
        for j in range(n):
            # 来回试探 看看 哪个适合
            for sign in [-1,1]:
                wsTest = ws.copy()

                print("wsTest[j]",wsTest[j])
                wsTest[j] += eps*sign
                yTest = xMat*wsTest
                rssE = rssError(yMat.A,yTest.A)
                if rssE < lowestError:
                    lowestError = rssE
                    wsMax = wsTest
        ws = wsMax.copy()
        returnMat[i,:]=ws.T

    return returnMat
def  PlotLine(X,wMat):
    
      fig = plt.figure()

      ax = fig.add_subplot(111)

      #number = 20
      ax.plot(wMat)
      
      print("X",X)


      #ax.plot(mat(X).T[:,1],wMat.T[:,1])

      plt.show()
def  TestStage():

	x,y= loaddataSet(filename)

	wMat=stageWise(x,y)

	PlotLine(x,wMat)

TestStage()