数据科学 6 参数估计与统计推断（概念）

主要内容：

• 假设检验与单样本T检验
• 两样本T检验
• 方差分析(分类变量和连续变量关系检验)
• 相关分析(两连续变量关系检验)
• 卡方检验(两分类变量关系检验)

6.1 参数估计

6.1.1 概念

1、总体与样本

• 总体 – 研究所感兴趣的所有个体组成总体
• 样本 – 从总体抽取的部分个体组成样本，样本用于对总体的某些指标作推断使用

2、参数和统计量

• 统计量由样本获取，用于对总体的参数进行估计
  

3、点估计

4、置信区间

95% 的置信区间代表参数估计值落在相应区间范围内的概率为95%，即总体参数值有95%的可能在估计值的置信区间内。

5、均值的标准误差

• 均值的标准误差是衡量估计的均值的变异程度
• 均值的标准误差随样本的标准差变化而变化
  • 样本的标准差用于衡量样本数据的变异程度
  • 均值的标准误差是衡量样本均值的变异程度
    

6、均值的置信区间

7、中心极限定理

• 为满足正态性假设，可以:
  • 验证总体分布是近似正态的
  • 应用中心极限定理.
    • 中心极限定理阐述了若样本的数据量足够大，样本均值的分布是近似正态的，
    • “足够大” 表示大于30 个样本.
      如果数据严重偏态，则需要更多的样本，如果数据本身是对称则不用

6.2 假设检验与单样本T检验

• 经验公式：
  k样本数与置信度α：
  k<100 α取10%
  100<k<500 α取5%
  500<k<100 α取1%
  2000左右 α取1‰
  数据再大，置信度就没有意义
  建立评分卡或统计模型，样本量不超过5000

统计学通过什么检验两个变量是否有关系？
检验均值差值是否为0（均值的差是否为0）

6.2.1 概念

1、t检验

• 检验0假设H0: μ = μ0, 首先计算t统计量:

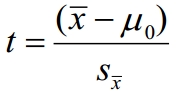
• 再根据t统计量相应的P值来判断是否拒绝原假设

2、拒绝域与接收域

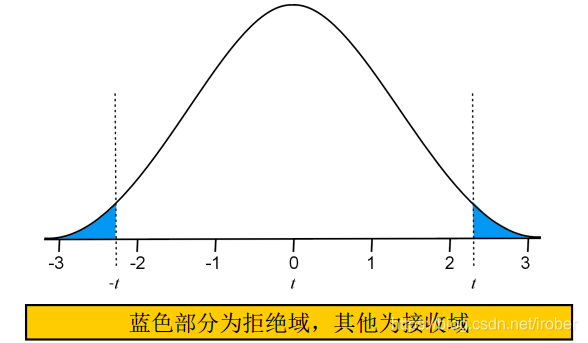
6.3 两样本T检验

6.3.1 两独立样本t检验

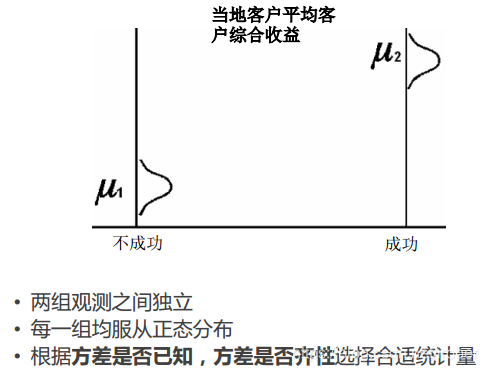
6.4 方差分析

(多分类,ANOVA)

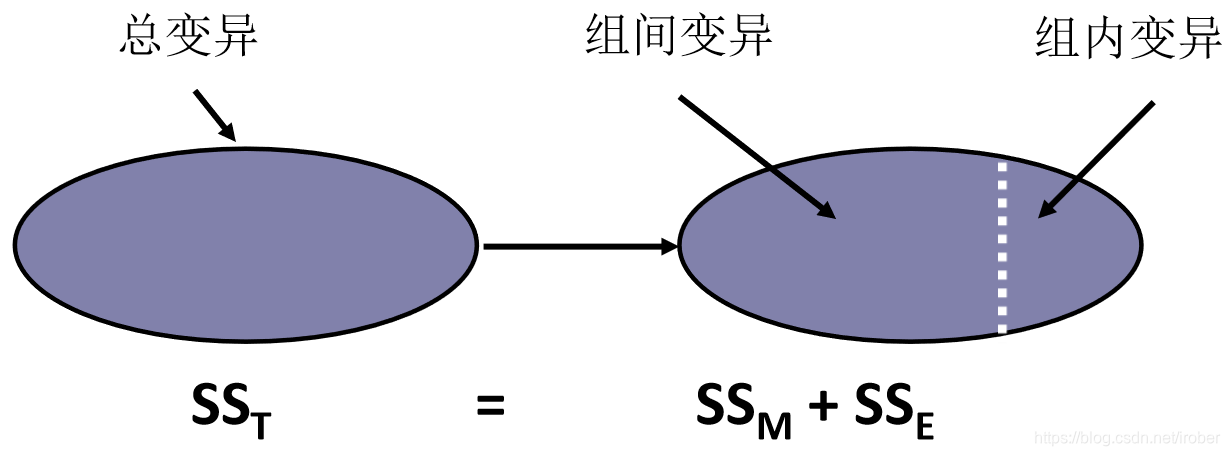
6.4.1 ANOVA分析的组间变异、组内变异和总变异

1、均值

（总体均值）

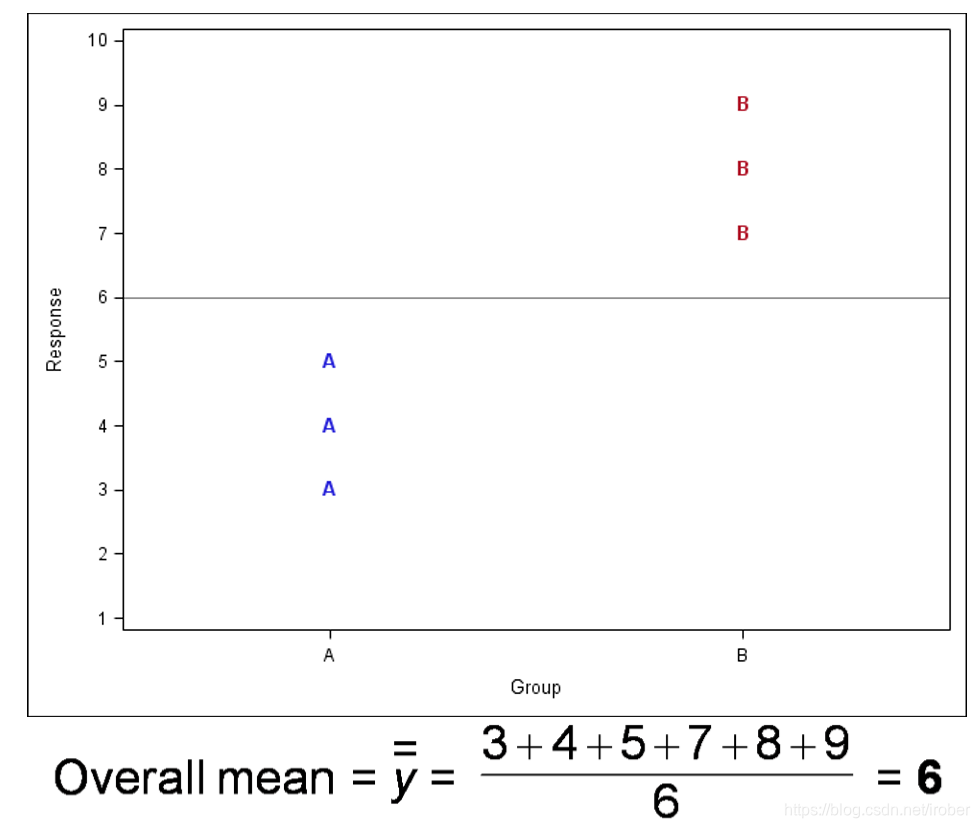
2、总变异

（样本值减均值的平方和）

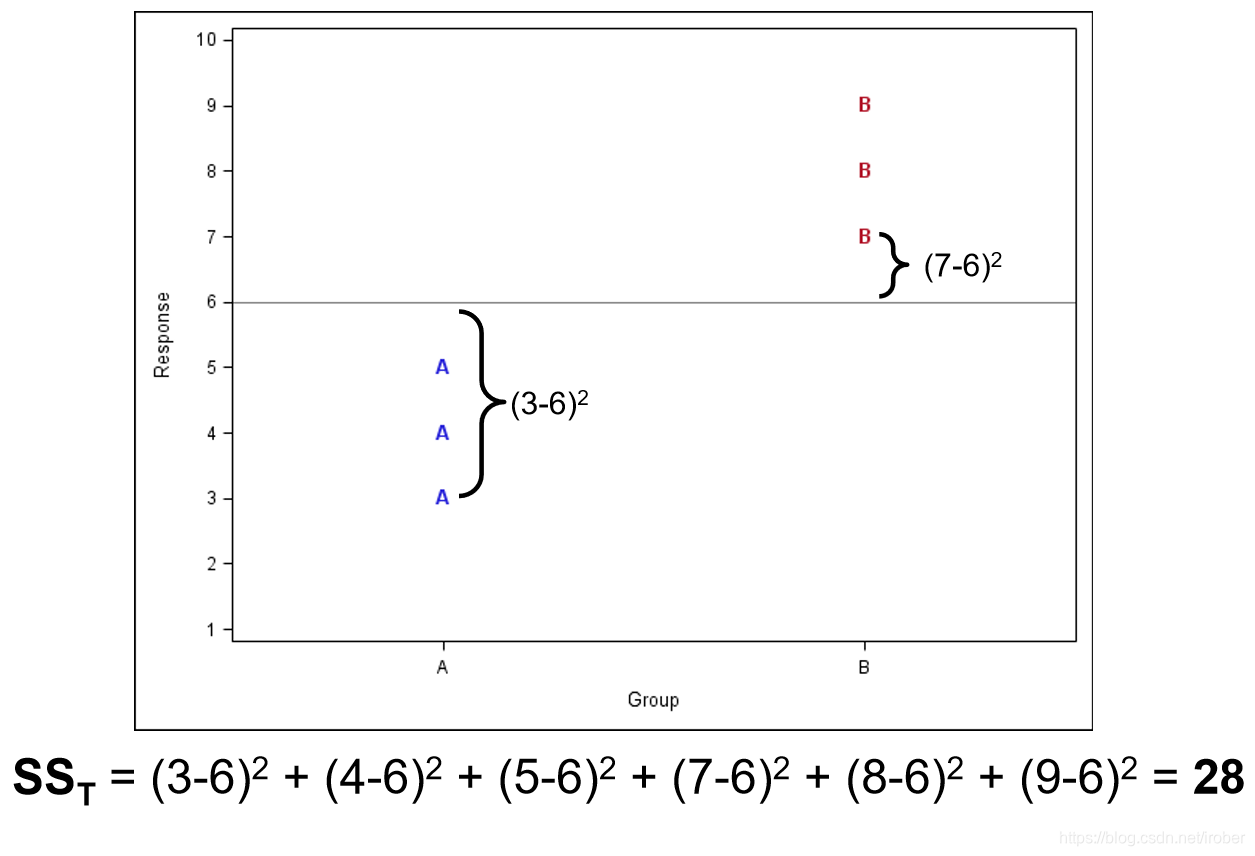
3、组内变异

（组内样本值减组内均值平方和）

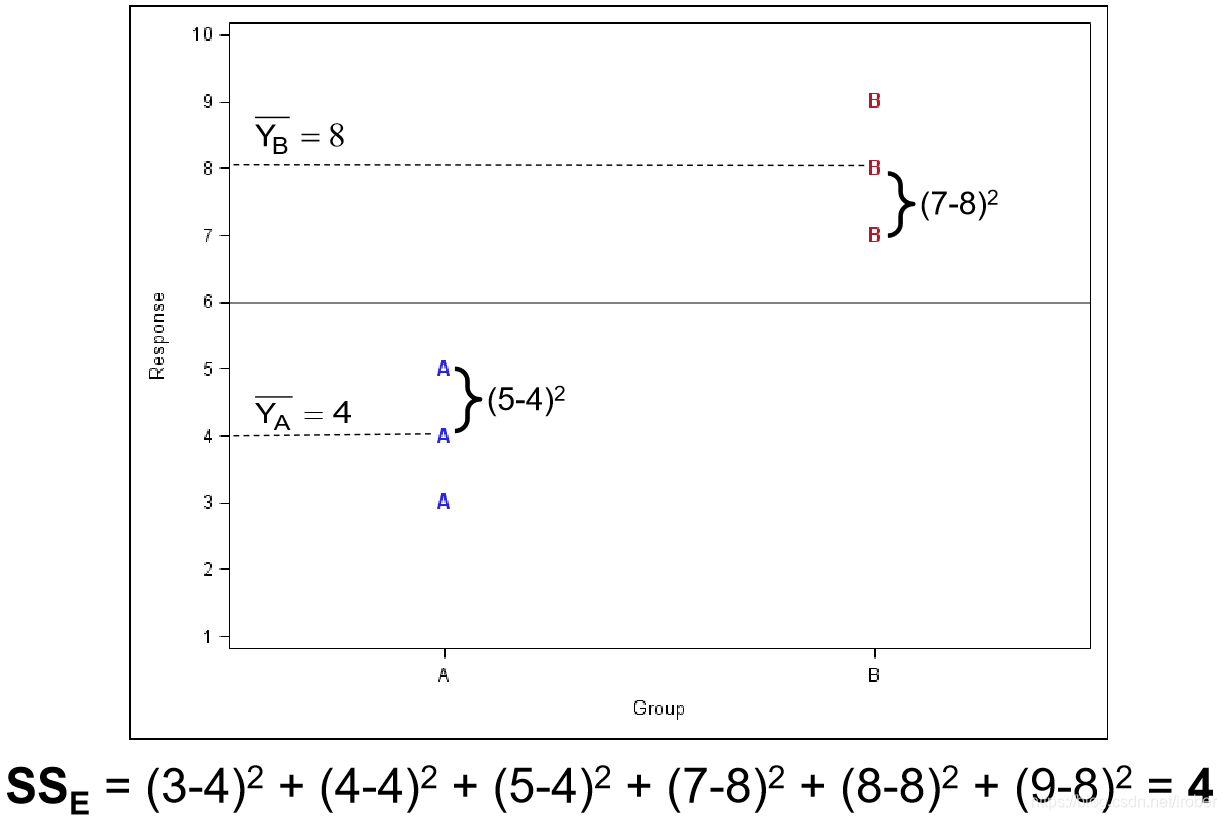
4、组间变异

分组均值减总体均值平方乘以组内样本数，再求和

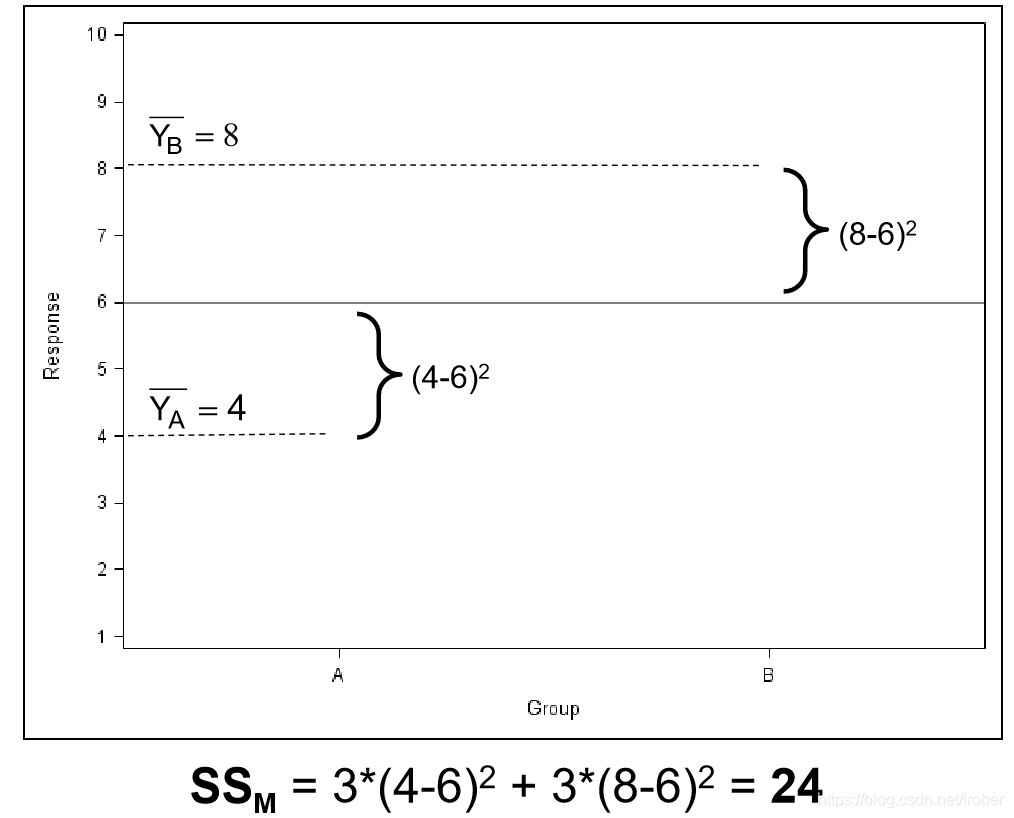
6.4.2 F统计量与显著水平$\alpha$=0.05

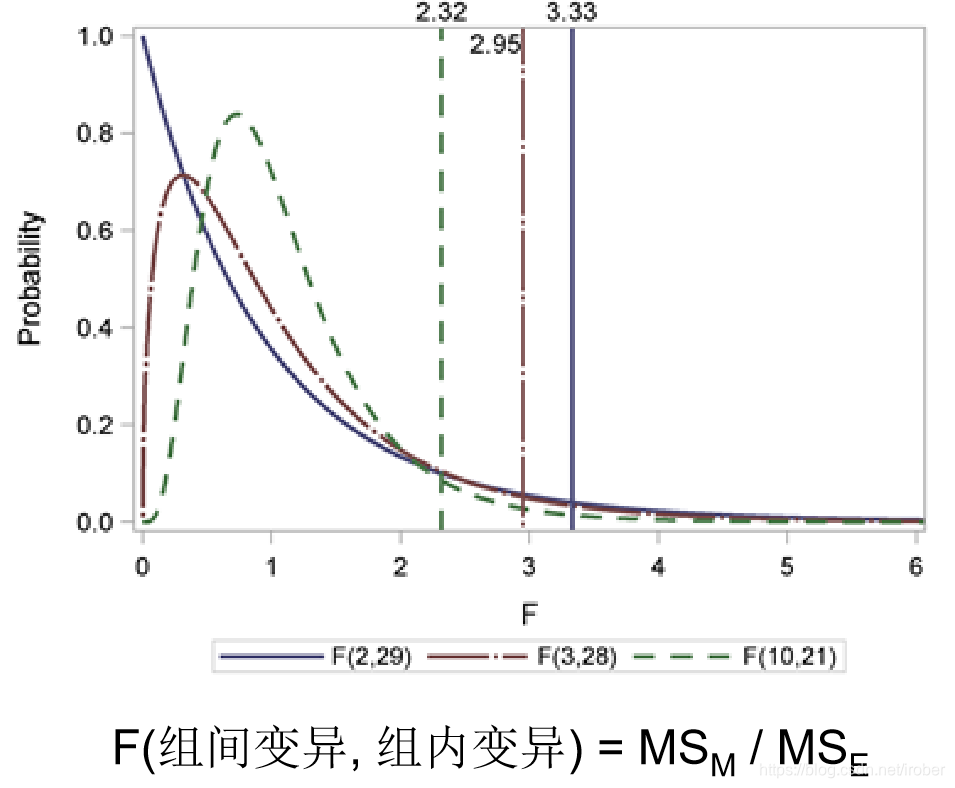
6.4.3 单因素方差分析模型

• 评估单因素方差分析结果
  • 注意数据中不同组的数据要服从独立性假设
  • 数据服从正态分布
  • 方差齐性要求

6.5 相关分析

（连续与连续）

6.5.1 三种相关系数

	相关关系是一种不完全确定的随机关系，当一个或几个变量的数值 被确定后，与之相应的另一个变量的值虽然不能确定，但是仍按照 某种依赖关系在一定的范围内变化。简单相关分析是研究两个变量 之间相关关系的方法。 

• PEARSON相关系数：参数方法、连续变量之间的相关
• SPEARMAN相关系数：非参方法、又称秩相关系数
• KENDALL相关系数：非参方法，序数变量之间的相关系数
• 

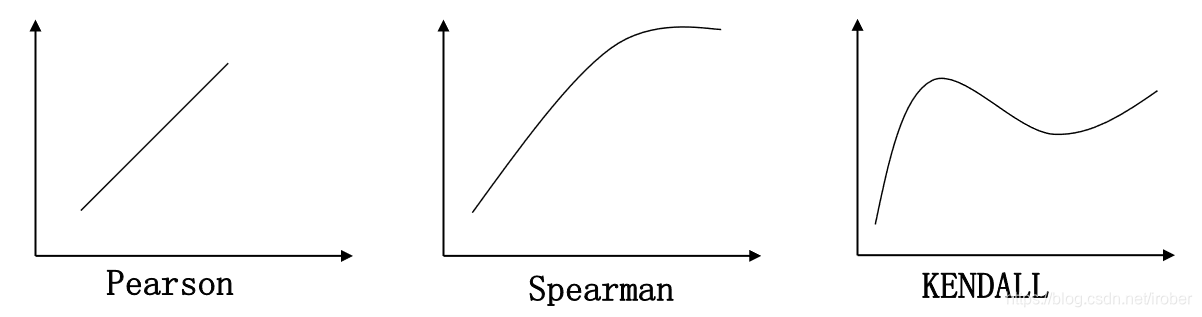
6.5.2 连续变量的线性相关分析

6.5.3 线性相关程度

6.5.3 相关系数的检验

6.6 卡方检验

（分类变量与分类变量）

6.6.1 列联表

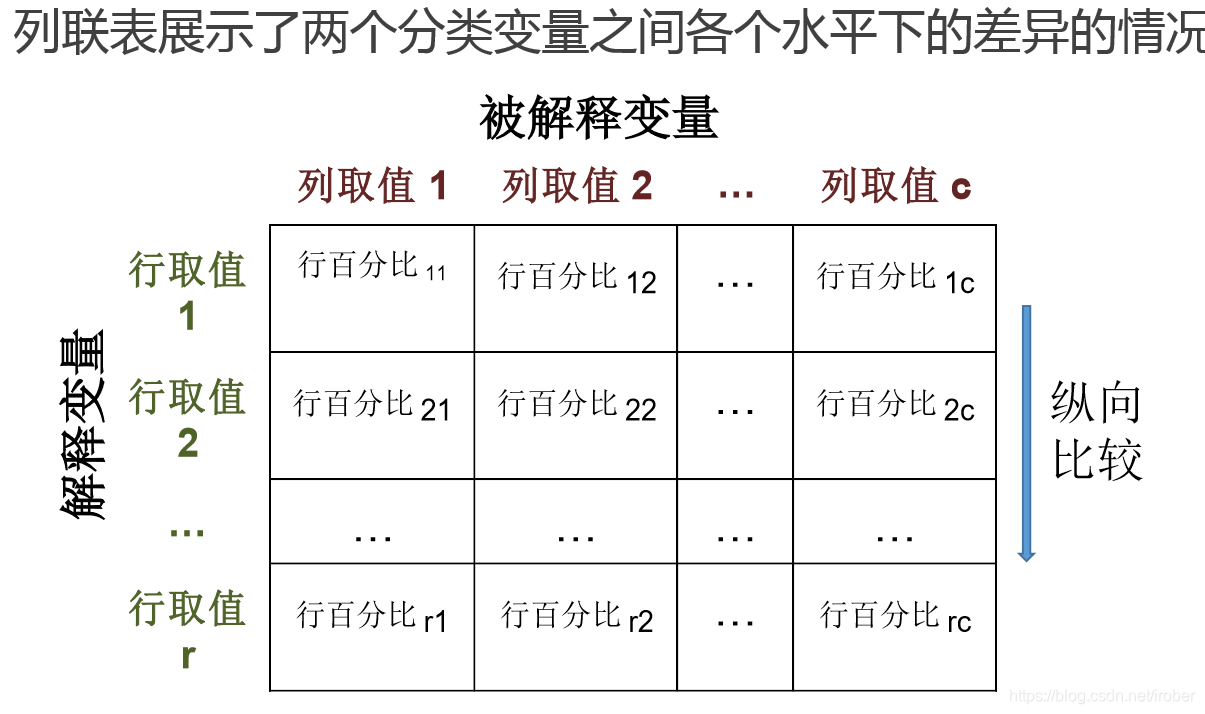
无相关性 与 存在相关性

6.6.2 列联分析的原假设与备选假

列联分析的原假设

• 客户重要性等级与是否成功入网无关系
• 即各级别客户入网的概率都一样
  列联分析的备择假设
• 客户重要性等级与是否成功入网有关系
• 即各级别客户入网的概率不一样

6.6.3 列联表分析

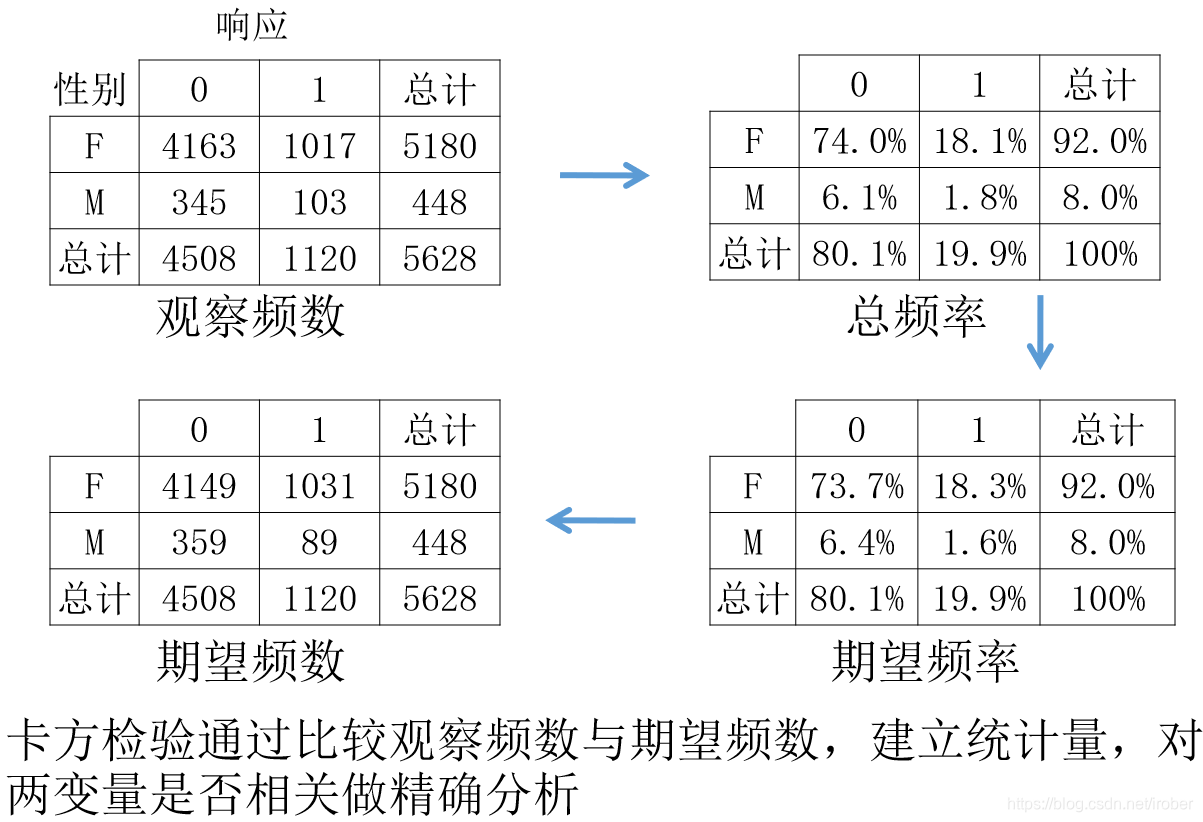
6.6.4 卡方检验

无关

• 实际频数= 期望频数

有关

• 实际频数$\ne$ 期望频数

                           期望频数计算公式：(行总* 列总) / 样本量