【模板】树的重心

最新推荐文章于 2024-07-25 14:00:47 发布

原创最新推荐文章于 2024-07-25 14:00:47 发布 · 962 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#图论 #算法 #树

树专栏收录该内容

4 篇文章

订阅专栏

树的重心是指使得最大子树结点数最小的点，具有多个性质，例如所有点到重心的距离和最小。在无权树中，以重心为根的所有子树大小不超过一半。本文讨论了如何找到树的重心，包括处理含有两个重心的情况，并提供了Codeforces和ICPC亚洲徐州区域赛的例题分析。

树的重心

树的重心也叫树的质心。对于一棵树n个节点的无根树，找到一个点，使得把树变成以该点为根的有根树时，最大子树的结点数最小。换句话说，删除这个点后最大连通块（一定是树）的结点数最小。

性质：

树中所有点到某个点的距离和中，到重心的距离和是最小的，如果有两个重心，他们的距离和一样。
把两棵树通过一条边相连，新的树的重心在原来两棵树重心的连线上。
一棵树添加或者删除一个节点，树的重心最多只移动一条边的位置。
一棵树最多有两个重心，且相邻。
对于无权树，以重心为根，所有子树的大小都不超过整棵树大小的一半，即其所有子树大小 $\le N/2$

带权树的重心：https://www.cnblogs.com/knife-rose/p/11258403.html

int T, n;
const int maxn = 1e5+7;
int sz[maxn], hs[maxn];
// sz[i]表示以i为根的子树的大小， hs[i]表示以i为根的重儿子(最大子树)的大小

struct edge{
    int next, v;
}e[maxn*2];
int cnt = 0;
int head[maxn];

int cent[2] = {0, 0}; // 重心
int ccnt = 0; // 重心个数

 
void addedge(int u, int v)
{
    e[cnt] = edge{head[u], v};
    head[u] = cnt++;
    e[cnt] = edge{head[v], u};
    head[v] = cnt++;
}
 
void dfs(int u, int fa)
{
    sz[u] = 1;
    hs[u] = 0;
    for(int i=head[u];i!=-1;i=e[i].next)
    {
        int v = e[i].v;
        if(v!=fa)
        {
            dfs(v, u);
            sz[u] += sz[v];
            hs[u] = max(hs[u], sz[v]);
            //cout << u << ' ' << v << ' ' << b[u] << endl;
        }
    }
    hs[u] = max(hs[u], n-sz[u]);
    if (hs[u] <= n / 2) {  // 依照树的重心的定义统计
    	cent[ccnt++] = cur;
  }
}

例题

Codeforces-Link Cut Tree
题目给定一棵树，要求删除一个边，再连接一条边，将其变为只有一个重心的树。

若只有一个重心则只需要把任意一个边断开连接一次就行。
若有2个重心分别为A、B
根据性质4：“一棵树最多有两个重心，且相邻”
可以想到，将重心A的一个子树与A断开，将该子树连接到重心B上（断开前每个重心所带的子树大小都为N/2，这么操作就会破坏破坏两重心的大小平衡）

#include<bits/stdc++.h>
using namespace std;

int T, n;
const int maxn = 1e5+7;
int a[maxn], b[maxn];

struct edge{
    int next, v;
}e[maxn*2];
int ccnt;
int head[maxn];
int cent[2] = {0, 0};
int cnt = 0, minsub = 0x3f3f3f3f;

void addedge(int u, int v)
{
    e[cnt] = edge{head[u], v};
    head[u] = cnt++;
    e[cnt] = edge{head[v], u};
    head[v] = cnt++;
}

void dfs(int u, int fa)
{
    a[u] = 1;
    b[u] = 0;
    for(int i=head[u];i!=-1;i=e[i].next)
    {
        int v = e[i].v;
        if(v!=fa)
        {
            dfs(v, u);
            a[u]+=a[v];
            b[u] = max(b[u], a[v]);
            //cout << u << ' ' << v << ' ' << b[u] << endl;
        }
    }
    b[u] = max(b[u], n-a[u]);
    if(b[u]<=n/2)
        cent[ccnt++] = u;
}


int main()
{
    cin >> T;
    while(T--)
    {
        cin >> n;
        cent[0] = cent[1] = 0;
        minsub = 0x3f3f3f3f;
        memset(head, -1, sizeof head);
        int u, v;
        for(int i=0;i<n-1;i++)
        {
            cin >> u >> v;
            addedge(u, v);
        }
        ccnt = 0;
        dfs(1, 0);
        
        
        if(ccnt==2){
            int v = e[head[cent[0]]].v;
            if(v==cent[1])
            {
                v = e[e[head[cent[0]]].next].v;
            }
            cout << cent[0] << ' ' << v << endl;
            cout << v << ' ' << cent[1] << endl;
        }
        else{
            cout << 1 << ' ' << e[head[1]].v << endl;
            cout << 1 << ' ' << e[head[1]].v << endl;
        }
//        cout << ccnt << endl;
//        cout << minsub << endl;
//        cout << cent[0] << ' ' << cent[1] << endl;
    }
    return 0;
}

求所有子树的重心

根据性质5：对于无权树，以重心为根，所有子树的大小都不超过整棵树大小的一半，即其所有子树大小 $\le N/2$

根据这个重心的定义可以知道一棵子树的重心必定在他自己所在的重子树中. 所以每次找到他的重儿子为根的子树的重心, 不符合的话就沿着重链往上走直至找到符合要求（ $s i z e [h s [p]] < = s i z e [x] / 2$ 以及 $s i z e [x] - s i z e [p] < = s i z e [x] / 2$ ）的重心.
（hs[x]表示x的重儿子）

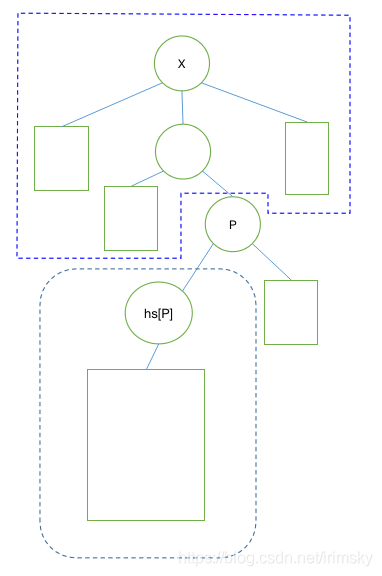
在x子树上对于p节点是否为重心的检查

例题：
2019 ICPC Asia Xuzhou Regional M - Kill the tree
题目要求找出所有子树的重心。两个重心的要按编号顺序输出。
对于两个重心的子树，因为我们是从底向上寻找第一个符合条件的重心就跳出，所以我们先找到深度较大的重心。根据性质4，可得两个重心是相邻的，所以第二个重心一定是这个重心的父节点，我们在输出时需要判断一下其父节点是否也符合重心的性质。

#include<bits/stdc++.h>
#define ms(a,v) memset((a), (v), sizeof(a));
#define rep(i,l,u) for(int (i)=(l);(i)<=(u);(i)++)
using namespace std;
#define ll long long
#define pr pair<int, int>
const ll maxn = 2e5+10;
const int mod = 1000000007;
struct edge{
    int v, next;
}e[maxn*2];

int head[maxn], ecnt;
int n;

int fa[maxn], sz[maxn], cent[maxn][2], hs[maxn], csz[maxn];

void add(int u, int v)
{
    e[ecnt].v = v;
    e[ecnt].next = head[u];
    head[u] = ecnt++;
}

void dfs(int x, int pre)
{
    fa[x] = pre;
    sz[x] = 1;
    cent[x][0] = x;
    int pson = x, maxx = 0;
    for(int i=head[x];i!=-1;i=e[i].next)
    {
        int v = e[i].v;
        if(v!=pre){
            dfs(v, x);
            if(sz[v] > maxx)
            {
                maxx = sz[v];
                pson = v;
            }
            sz[x] += sz[v];
        }
    }
    hs[x] = pson;
    if(pson == x) {
        csz[x] = 1;
        return;
    }
    int p = cent[pson][0];
    // cout << pson << endl;
    while(p != fa[x])
    {
        if(sz[hs[p]]*2<=sz[x]&&(sz[x]-sz[p])*2<=sz[x]){
            cent[x][csz[x]++] = p;
            break;
        }
        p = fa[p];
    }
}



int main()
{
    cin >> n;
    int u, v;
    for(int i=1;i<=n;i++)
        head[i] = -1;
    
    for(int i=0;i<n-1;i++)
    {
        cin >> u >> v;
        add(u, v);
        add(v, u);
    }
    dfs(1, 0);
    for(int i=1;i<=n;i++){
        if(fa[cent[i][0]] && sz[i] == 2 * sz[cent[i][0]])
            cent[i][csz[i]++] = fa[cent[i][0]];
        if(csz[i]==1)
            printf("%d\n", cent[i][0]);
        else{
            sort(cent[i], cent[i]+2);
            printf("%d %d\n", cent[i][0], cent[i][1]);
        }
    }
    return 0;
}