机器学习笔记12-PCA(主成分分析)

PCA降维算法

已标注和未标注的数据上都有降维技术。这里我们主要关注未标注数据上的降维技术，该技术也可以用于已标注数据。

第一种降维的方法称为主成分分析(Principal Component Analysis,PCA)。在PCA中，数据从原来的坐标系转换到了新的坐标系，新坐标系的选择是由数据本身决定的。第一个新坐标轴选择的是原始数据中方差最大的方向，第二个新坐标轴的选择和第一个新坐标轴正交且具有最大方差的方向。该过程一直重复，重复次数为原始数据中特征的数目。

另一种降维技术是因子分析。在因子分析中，我们假设在观察数据的生成中有一些观察不到的隐变量。假设观察数据是这些隐变量和某些噪声的线性组合。

还有一种降维技术是独立成分分析(Independent Component Analysis,ICA)。

PCA的伪代码大致如下:

那么如何选择N的大小呢？下图为总方差的百分比，我们发现，在开始几个主成分后，方差会迅速下降。

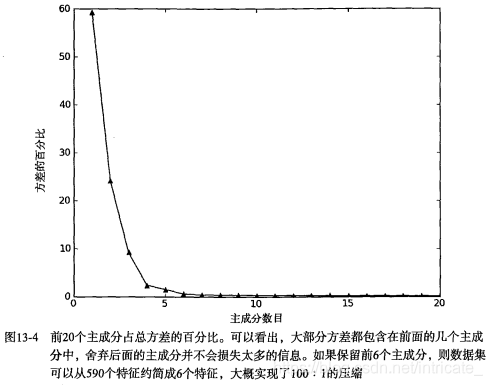
上图表明了，如果保留前6个而去除后584个主成分，我们就可以实现大概100：1的压缩比。下图为成分对应的方差百分比和累计方差百分比。

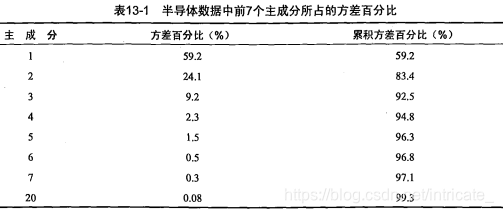
Python代码如下：

from numpy import *

def loadDataSet(fileName, delim='\t'):
    fr = open(fileName)
    stringArr = [line.strip().split(delim) for line in fr.readlines()]
    datArr = [list(map(float,line)) for line in stringArr]
    return mat(datArr)

'''
pca(主成分分析法)降维
@param dataMat：数据集(m,n)，n为特征数
@param topNfeat：降维后保留的特征数目
'''
def pca(dataMat, topNfeat=9999999):
    meanVals = mean(dataMat, axis=0)  # 按列求和得到每个特征的平均值
    meanRemoved = dataMat - meanVals  # 去除平均值
    covMat = cov(meanRemoved, rowvar=0)  # 计算协方差矩阵，rowvar=0，代表一行代表一个样本，计算出的类型是array
    eigVals,eigVects = linalg.eig(mat(covMat)) # 求解协方差矩阵的特征值和特征向量，使用linalg.eig()函数，其中特征值为 (1,n)，特征向量为 (n,n)
    eigValInd = argsort(eigVals)       # 特征值从小到大排序，得到排序索引
    eigValInd = eigValInd[:-(topNfeat+1):-1]  # 得到想要的前topNfeat大的特征值的索引
    redEigVects = eigVects[:,eigValInd]       # 得到想要的前topNfeat大的特征向量，(n,topNfeat)
    lowDDataMat = meanRemoved * redEigVects   # 将数据转化到新的空间，得到降维后的矩阵，(m,topNfeat)
    reconMat = (lowDDataMat * redEigVects.T) + meanVals  # 在新空间下，重构原始数据矩阵，(m,n)
    return lowDDataMat, reconMat  # 返回降维后的矩阵、在新空间下的原始数据矩阵

# datMat = loadDataSet('testset.txt')  # dataMat为(m,n)
# lowDataMat, reconMat = pca(datMat,1)  # 降维成一个维度
# import matplotlib.pyplot as plt
# fig = plt.figure() # 绘图显示原始数据和pca降维后的新空间下的数据
# ax = fig.add_subplot(111)
# ax.scatter(datMat[:,0].flatten().A[0], datMat[:,1].flatten().A[0], marker='^', s=50)  # 原始数据，三角形蓝点
# ax.scatter(reconMat[:,0].flatten().A[0], reconMat[:,1].flatten().A[0], marker='o', s=50, c='red')  # 新空间下的数据，圆形红点
# plt.show()

# 将NaN替换成平均值的函数（该函数不能解决一个特征都是NaN这样的情况）
def replaceNanWithMean(): 
    datMat = loadDataSet('secom.data', ' ')
    numFeat = shape(datMat)[1]
    for i in range(numFeat): # 对于每一列（每一个特征）
        meanVal = mean(datMat[nonzero(~isnan(datMat[:,i].A))[0],i]) # nonzero(~isnan(datMat[:,i].A))[0] 返回非NaN的行的索引
        datMat[nonzero(isnan(datMat[:,i].A))[0],i] = meanVal  # 把数据集中每一列的所有NaN值替换成每一列中非NaN数据的平均值
    return datMat

# 利用PCA对半导体制造数据降维（590个特征）
dataMat = replaceNanWithMean()
meanVals = mean(dataMat, axis=0)  # 按列求和得到每个特征的平均值
meanRemoved = dataMat - meanVals  # 去除平均值
covMat = cov(meanRemoved, rowvar=0)  # 计算协方差矩阵，rowvar=0，代表一行代表一个样本，计算出的类型是array
eigVals,eigVects = linalg.eig(mat(covMat)) # 求解协方差矩阵的特征值和特征向量，使用linalg.eig()函数，其中特征值为 (1,n)，特征向量为 (n,n)
print(eigVals)  # 发现最前面的15个特征值数量级大于10^5，这告诉我们只有部分重要特征
eigValInd = argsort(eigVals)
eigValInd = eigValInd[::-1]  # list反转，从大到小
sortedEigVals = eigVals[eigValInd]
total = sum(sortedEigVals)
varPercentage = sortedEigVals/total*100  # 方差的百分比

import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(range(1, 21), varPercentage[:20], marker='^')
plt.xlabel('Principal Component Number')  # 主成分数目
plt.ylabel('Percentage of Variance')  # 方差的百分比
plt.show()  # 观察图可以发现，只保留6个特征即可

# 因此，调用pca(dataMat,6)可以将590维的特征降成6维