计数动态规划——所有路径数

//计数型动态规划 
#include<iostream>
#include<cstdio>
using namespace std;
int m, n;//m 行 n 列 
int f[100][100];//走到（i,j）的路径总数 
int main() {
	cin >> m >> n;
	for (int i = 0;i < m;i++) {
		for (int j = 0;j < n;j++) {
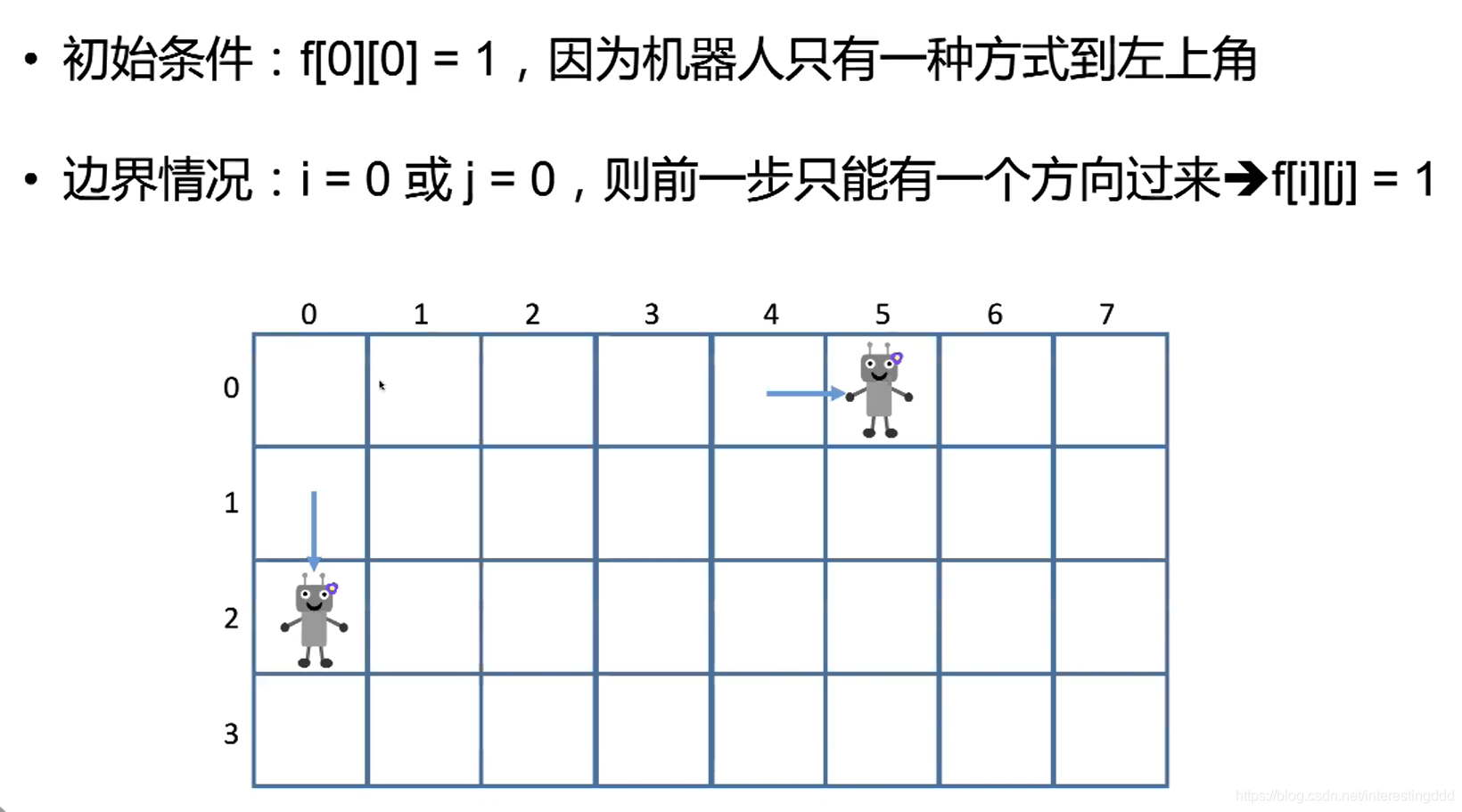
			if (i == 0 || j == 0) f[i][j] = 1;//初始化原点路径为 1,而且由于只能向右、向下走,i=0或j=0时路径数都为 1！ 
			else f[i][j] = f[i - 1][j] + f[i][j - 1];//关系式 
		}
	}
	cout << f[m - 1][n - 1];//右下角路径（此题其实很有递归的味道~） 
	return 0;
}