//递推思想
#include<iostream>
#include<cstdio>
using namespace std;
int a[100005], n, k;
int main() {
cin >> n >> k;
a[0] = 1;
//对前 k 阶随便跳(1 到 k 步)
for (int i = 1;i <= k;i++) {
for (int j = 0;j < i;j++) {
a[i] += a[j];
}
a[i] %= 100003;
//提前取模不会影响结果,同时避免结果一不小心超出 int 范围就不好了
}
//最好根据简单情况找一下规律,结汇更好理解接下来的代码(本菜鸡也晕了好长时间~)
for (int i = k+1;i <= n;i++) {
for (int j = i - k;j < i;j++) {
a[i] += a[j];
}
a[i] %= 100003;
}
cout << a[n] << endl;
return 0;
}
懒懒的我从洛谷题解”盗“了规律,并不难理解:
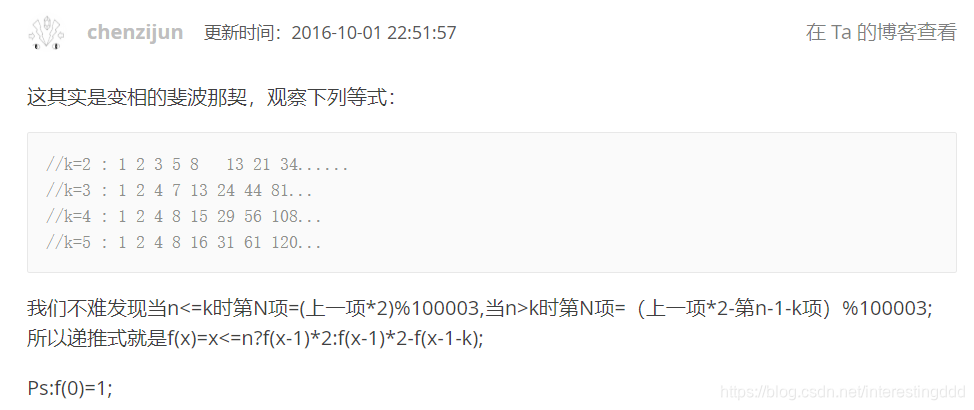
(感谢 chenzijun 大佬!)





 本文通过递推思想解析了一道跳跃游戏的算法题目,介绍了如何利用动态规划求解前k阶的任意跳跃和之后的限制跳跃问题,确保结果在模100003下的正确性。代码清晰易懂,适合初学者学习递推和动态规划的应用。
本文通过递推思想解析了一道跳跃游戏的算法题目,介绍了如何利用动态规划求解前k阶的任意跳跃和之后的限制跳跃问题,确保结果在模100003下的正确性。代码清晰易懂,适合初学者学习递推和动态规划的应用。
















 434
434

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








