深入了解网络流——RXD大佬上课笔记

$$\color{gray}{一、几个概念}$$

流网络G(V,E) : 是一个有限的向图，每条边(u,v)∈E都有一个非负实数的容量c(u,v)。如果 u,v∉E，我们假设c(u,v)=0。

在图中，我们区别两个顶点 源点s和汇点t 。

网络流是对于所有结点u和v都满足以下性质的实数函数f:v*v→R:

• 容量限制： f(u,v)≤c(u,v)
• 斜对称： f(u,v)=−f(u,v)
• 流守恒：除了 s，t ，结点均满足Σ(v∈V)f(u,v)=0。

边的 剩余流量 c_f(u,v)=c(u,v)−f(u,v)。它定义了剩余网络 G_f(V,E_f)，

根据斜对称性我们知道，增加 u至v的流量同时要减少 v至u的流量，因此我们考虑 净流量 。这就表现为增加一条边的流量时，
我们减小它剩余同时增加其 反向边 的剩余流量。当我们沿反向边增加时，就表现为原边的 退流 。

增广路是一条路径p=(s,u1,u2,⋯,um,t):
并且k=min{c(fu,vu)|v(u,v)}∈p>0，表示 我能沿着这条路径传送 k的流量 。

网络的流: f=Σ(s,v)∈E f(s,u)=Σ(v,t)∈Ef (v,t);

最大流是网络中能达到的最大网络流，根据 增广路定理 我们知道网络达到最大流当且仅剩余网络中没有增广路。

边的费用 为每条边具有的费用 w(u,v)，表示在这条边上每流过1单位的流量，需要 w(u,v) 的费用。

最小费用大流 是保证最大流的情况下，使得费用小；

最大费用可行流 只需要费用最大，而不保证流。如果每次寻找用最大的增广路进行，只需要在不存费为正时停止算法即可。

割是边的集合，删去中所有将使得 s无法到达 t。割边 是集合中的一 条边。

最小割是容量和最小的割。

我们根据 最大流小割定理 知道最大流等于小割。

一条边(u,v)能属于某个最小割当且仅剩余网络中不存在从 u到v最小剩余流量大于 0的路径。

最小割将点划分为两个集合，我们称包含 s的为 S集，包含 t的为 T集

$$\color{gray}{二、几种算法}$$

常见的网络流算法有 Edmonds-Karp、Dinic 和 ISAP等。

1、Edmonds-Karp

int graph::Edmonds_Karp(int start, int end, int remain_g[][1000], int current_g[][1000])//按BFS找增广路径(即每次找边数最短的)实现Ford_Fulkerson方法
{
    for (int i = 0; i < Pnum; i++)
        for (int j = 0; j < Pnum; j++)
        {
            if (edge[i][j] == INF)
                remain_g[i][j] = 0;
            else
                remain_g[i][j] = edge[i][j];
        }
    int max_flow = 0;
    while (1)
    {
        int visit[1000];
        int pre[1000];//记录节点的前驱，好找路径,其实这里的visit可以不要,就用pre
        memset(visit, 0, sizeof(visit));
        memset(pre, 0, sizeof(pre));
        //bfs在残留网络中找增广路径
        queue<int> q;
        q.push(start);
        while (!q.empty())
        {
            int temp_point = q.front();
            q.pop();
            if (temp_point == end)
                break;
            for (int i = 0; i < Pnum; i++)
            {
                if (remain_g[temp_point][i] > 0 && !visit[i])
                {
                    q.push(i);
                    pre[i] = temp_point;
                    visit[i] = 1;
                }
            }
        }
        //更新残留网络
        if (pre[end] == 0)//end的前驱没有更新，证明没有增广路径了
            break;
        int min = INF;
        for (int temp_point = end; temp_point != start; temp_point = pre[temp_point])
            min = zzMin(remain_g[pre[temp_point]][temp_point], min);
        for (int temp_point = end; temp_point != start; temp_point = pre[temp_point])
        {
            remain_g[pre[temp_point]][temp_point] -= min;
            remain_g[temp_point][pre[temp_point]] = min;//此为负向边
        }
        max_flow += min;
    }
    return max_flow;
}

//remain_g为找到最大流后得到的残留网络
bool graph::Find_Min_Cut(int start,int remain_g[][1000], vector<int> &s_set, vector<int> &t_set)
{
    int visit[1000];
    memset(visit, 0, sizeof(visit));
    queue<int> s;
    s.push(start);
    while (!s.empty())
    {
        int temp_point = s.front();
        s.pop();
        for (int i = 0; i < Pnum; i++)
            if (remain_g[temp_point][i] > 0 && !visit[i])
            {
                s.push(i);
                visit[i] = 1;
                s_set.push_back(i);
            }
    }
    for (int i = 0; i < Pnum; i++)
        if (!visit[i])
            t_set.push_back(i);
    return true;
}

2、Dinic（有空再来补注释吧……）

void Add_Edge(int x,int y,int f){
    E[cnt]=(Edge){y,f,Last[x]};Last[x]=cnt++;
    E[cnt]=(Edge){x,0,Last[y]};Last[y]=cnt++;
}
bool bfs(){
    memset(Dis,-1,sizeof(Dis));Dis[S]=1;
    int f=1,w=0;Q[1]=S;
    while (f>w){
        int x=Q[++w];
        for (int i=Last[x],y;~i;i=E[i].nxt)
            if (E[i].f&&Dis[y=E[i].y]==-1) Dis[y]=Dis[x]+1,Q[++f]=y;
    }
    return Dis[T]!=-1;
}
int dinic(int x,int flow){
    if (x==T||!flow) return flow;
    int res=0;
    for (int i=Last[x],y;~i;i=E[i].nxt)
        if (E[i].f&&Dis[y=E[i].y]==Dis[x]+1){
            int tmp=dinic(y,min(E[i].f,flow));
            E[i].f-=tmp,E[i^1].f+=tmp,flow-=tmp,res+=tmp;
        }
    if (!res) Dis[x]=-1;
    return res;
}

class BoardPainting{
public:
    int minimalSteps(Vs s){
        memset(Last,-1,sizeof(Last));
        n=s.size();
        m=s[0].length();
        For(i,0,n) For(j,0,m) pt[i][j]=++tot;
        S=++tot,T=++tot;
        For(i,0,n) For(j,0,m)
            if (s[i][j]=='#'){
                int c0=0,c1=0;
                For(k,0,4){
                    int x=i+dx[k],y=j+dy[k];
                    if (0<=x&&x<n&&0<=y&&y<m&&s[x][y]=='#'){
                        Add_Edge(pt[i][j],pt[x][y],1);
                    } else k&1?c0++:c1++;
                }
                Add_Edge(S,pt[i][j],c0);
                Add_Edge(pt[i][j],T,c1);
            }
        while (bfs()) res+=dinic(S,oo);
        return res/2;
    }
} Test;

3、ISAP

struct ISAP  
{  
    int n,m,s,t;  
    vector<Edge>edges;  
    vector<int>G[N];  
    bool vis[N];  
    int d[N],cur[N];  
    int p[N],num[N];//比Dinic算法多了这两个数组，p数组标记父亲结点，num数组标记距离d[i]存在几个  
    void addedge(int from,int to,int cap)  
    {  
        edges.push_back(Edge(from,to,cap,0));  
        edges.push_back(Edge(to,from,0,0));  
        int m=edges.size();  
        G[from].push_back(m-2);  
        G[to].push_back(m-1);  
    }  

    int Augumemt()  
    {  
        int x=t,a=INF;  
        while(x!=s)//找最小的残量值  
        {  
            Edge&e=edges[p[x]];  
            a=min(a,e.cap-e.flow);  
            x=edges[p[x]].from;  
        }  
        x=t;  
        while(x!=s)//增广  
        {  
            edges[p[x]].flow+=a;  
            edges[p[x]^1].flow-=a;//更新反向边。  
            x=edges[p[x]].from;  
        }  
        return a;  
    }  
    void bfs()//逆向进行bfs  
    {  
        memset(vis,0,sizeof(vis));  
        queue<int>q;  
        q.push(t);  
        d[t]=0;  
        vis[t]=1;  
        while(!q.empty())  
        {  
            int x=q.front();q.pop();  
            int len=G[x].size();  
            for(int i=0;i<len;i++)  
            {  
                Edge&e=edges[G[x][i]];  
                if(!vis[e.from]&&e.cap>e.flow)  
                {  
                    vis[e.from]=1;  
                    d[e.from]=d[x]+1;  
                    q.push(e.from);  
                }  
            }  
        }  
    }  

    int Maxflow(int s,int t)//根据情况前进或者后退，走到汇点时增广  
    {  
        this->s=s;  
        this->t=t;  
        int flow=0;  
        bfs();  
        memset(num,0,sizeof(num));  
        for(int i=0;i<n;i++)  
            num[d[i]]++;  
        int x=s;  
        memset(cur,0,sizeof(cur));  
        while(d[s]<n)  
        {  
            if(x==t)//走到了汇点，进行增广  
            {  
                flow+=Augumemt();  
                x=s;//增广后回到源点  
            }  
            int ok=0;  
            for(int i=cur[x];i<G[x].size();i++)  
            {  
                Edge&e=edges[G[x][i]];  
                if(e.cap>e.flow&&d[x]==d[e.to]+1)  
                {  
                    ok=1;  
                    p[e.to]=G[x][i];//记录来的时候走的边，即父边  
                    cur[x]=i;  
                    x=e.to;//前进  
                    break;  
                }  
            }  
            if(!ok)//走不动了，撤退  
            {  
                int m=n-1;//如果没有弧，那么m+1就是n，即d[i]=n  
                for(int i=0;i<G[x].size();i++)  
                {  
                    Edge&e=edges[G[x][i]];  
                    if(e.cap>e.flow)  
                        m=min(m,d[e.to]);  
                }  
                if(--num[d[x]]==0)break;//如果走不动了，且这个距离值原来只有一个，那么s-t不连通，这就是所谓的“gap优化”  
                num[d[x]=m+1]++;  
                cur[x]=0;  
                if(x!=s)  
                    x=edges[p[x]].from;//退一步，沿着父边返回  
            }  
        }  
        return flow;  
    }  
};

$$\color{gray}{三、几道例题}$$

例题一：TopCoder SRM 575 Div 1 - Problem 1000 Tunnels

题目大意:

• 紫比利有一块大草原，是个n·m的网格图，一些上有城镇。 • 于是他想划分出一些牧区 FA 展畜牧业。但是他喜欢弯的，所以有一些要求：
•每个牧区必须呈 L形，即面积为 3的转角；
• 将网格黑白染色，左上角为将网格黑白染色， 左上角为将网格黑白染色， 左上角为L形的转角处必须是黑色；
• L形可以进行旋转；
• 问最多能划分出少牧区。

分析：
如果我们只是按照题目的意思把图黑白染色话，会发现边不太好连也不知道怎么保证连出来的是 L形。

然而我们稍微观察一下，就可以发现：（其中 2表示黑点）

如果将图划分成这样，那么一个合法L形一定是1连到2连到3。

于是我们把图分为1,2,3三块，并将每个点拆点，中间连流量为1的边。
然后S向1中的点连边，1向相邻的2中的点连边，2向相邻的3中的点连边， 3中的点向T连边。
然后跑最大流输出答案即可，每一流量代表一个L形。

例题二：Sphere Online Judge - 839 Optimal Marks(OPTM)

题目大意:
给出一个无向图G = (V, E)，每个点v以一个有界非负整数作为标号lv，每条边e = (u, v)的权W_e定义为该边的两个端点的标号的异或值，即W_e =l_u xor l_v。
现已知其中部分点的标号，求使得该图的总边权和最小的标号赋值。即最小化：

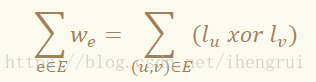
N≤500,M≤3000

分析:
先把那些和所有已知点都不在同一个连通块的标号设为 0，这样的 话这些点之间的边权就不用计入目标函数了。
我们发现 xor不太好 直接 处理，先考察一下 xor的定义 ：

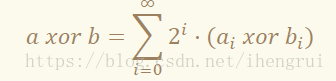
其中 ai表示 a的二进制表达式第 i位的值， bi的意义类似。
因为二进制位 互不影响，所以我们可把每分开 考虑，按位加和：

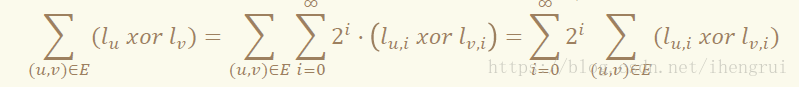
于是，主算法就依次处理各个二进制位而将子问题化归为：

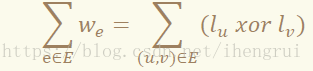
式子和之前是一样的，但限制条件加强了： ∀u∈V.lu∈{0,1}。
• 即对于每个点 ，都只有 两种取值，可以看成是 要将 点集划分成两类。在这 种分类思想的指导下 ，我们可以发现 ：对于每条边 的两 个端点 ，若它们同 类则边权无值 ；若它们异有1。
我们发现，这和最小割的性质非常相似：也是将点集分为两类的容量是 S和T之间的边容量和；优化目标同样是最小。

• 下面我们来形式化地表达一。
•我们要求最后将具有标号 0的点归到 S集，具有标号 1的点归到 T集。
• 对于已经有标号的点 v，如果它具有标号 0，则增加有向边(s,v)∈EN，并 且使得 c(s,v)=∞,保证它在 S集中。类似地，如果它具有标号 1，则增加有 向边 v,t∈EN，并且使得c(v,t)=∞。
• 对于每条原图中的边 (u,v)∈E，我们在 网络 中增加两条容量分别为 c(u,v)=c(v,u)=1的有向边(u,v)∈EN,(u,v)∈EN。
• 这样的话，如果一个未确定标号点要被分到 S集，则必须要割掉它和所 有和它相连的且被分在
• 设最大的标号为 U，则复杂度为O(logU·MaxFlowN)。

最后贴下代码：

#include <bits/stdc++.h>
#include <ext/pb_ds/priority_queue.hpp>
#include <tr1/unordered_map>
using namespace std;
using __gnu_pbds::pairing_heap_tag;
#define x first
#define y second
#define Hash unordered_map
#define clr(x,b) memset((x),(b),sizeof(x))
typedef unsigned long long uLL;
typedef long long LL;
typedef pair<int, int> pii;
typedef pair<double, double> pdd;
typedef __gnu_pbds::priority_queue<pii, greater<pii>, pairing_heap_tag> Heap;
typedef Heap::point_iterator Hit;
const Hit null;
const double PI = acos(-1);
const LL LINF = 0x3f3f3f3f3f3f3f3fll;
const int INF = 0x3f3f3f3f;
const double eps = 1e-8;
const int MOD = 1 << 16;
#define prln(x) cout<<#x<<" = "<<x<<endl
#define pr(x) cout<<#x<<" = "<<x<<" "

const int maxn = 600;
struct Edge { int from, to, cap, flow; };
struct ISAP {
    int n, m, s, t;
    vector<Edge> edges;
    vector<int> G[maxn];
    bool vis[maxn];
    int d[maxn];
    int cur[maxn];
    int p[maxn];
    int num[maxn];
    void add_edge(int from, int to, int cap) {
        edges.push_back((Edge){from, to, cap, 0});
        edges.push_back((Edge){to, from, 0, 0});
        m = edges.size();
        G[from].push_back(m-2);
        G[to].push_back(m-1);
    }
    bool bfs() {
        memset(vis, 0, sizeof(vis));
        queue<int> q;
        q.push(t);
        vis[t] = 1;
        d[t] = 0;
        while(!q.empty()) {
            int x = q.front(); q.pop();
            for(int i = 0; i < G[x].size(); i++) {
                Edge& e = edges[G[x][i]^1];
                if(!vis[e.from] && e.cap > e.flow) {
                    vis[e.from] = 1;
                    d[e.from] = d[x] + 1;
                    q.push(e.from);
                }
            }
        }
        return vis[s];
    }

    void doit(int ans[])
    {
        clr(vis, 0);
        queue<int>q;
        q.push(s);
        vis[s] = 1;
        d[s] = 0;
        while (!q.empty())
        {
            int x = q.front();
            ans[x]+=1;
            q.pop();
            for (int i = 0; i < G[x].size(); i ++ )
            {
                Edge& e = edges[G[x][i]];
                if (!vis[e.to] && e.cap > e.flow)
                {
                    vis[e.to] = 1;
                    q.push(e.to);
                }
            }
        }
    }




    void init(int n) {
        this->n = n;
        for(int i = 0; i < n; i++) G[i].clear();
        edges.clear();
    }
    void clear_flow() {
        for(int i = 0; i < edges.size(); i++) edges[i].flow = 0;    
    }
    int augment() {
        int x = t, a = INF;
        while(x != s) {
            Edge& e = edges[p[x]];
            a = min(a, e.cap-e.flow);
            x = edges[p[x]].from;
        }
        x = t;
        while(x != s) {
            edges[p[x]].flow += a;
            edges[p[x]^1].flow -= a;
            x = edges[p[x]].from;
        }
        return a;
    }
    int maxflow(int s, int t) {
        this->s = s; this->t = t;
        int flow = 0;
        bfs();
        memset(num, 0, sizeof(num));
        for(int i = 0; i < n; i++) num[d[i]]++;
        int x = s;
        memset(cur, 0, sizeof(cur));
        while(d[s] < n) {
            if(x == t) {
                flow += augment();
                x = s;
            }
            int ok = 0;
            for(int i = cur[x]; i < G[x].size(); i++) {
                Edge& e = edges[G[x][i]];
                if(e.cap > e.flow && d[x] == d[e.to] + 1) {
                    ok = 1;
                    p[e.to] = G[x][i];
                    cur[x] = i;
                    x = e.to;
                    break;
                }
            }
            if(!ok) {
                int m = n-1;
                for(int i = 0; i < G[x].size(); i++) {
                    Edge& e = edges[G[x][i]];
                    if(e.cap > e.flow) m = min(m, d[e.to]);
                }
                if(--num[d[x]] == 0) break;
                num[d[x] = m+1]++;
                cur[x] = 0;
                if(x != s) x = edges[p[x]].from;
            }
        }
        return flow;
    }

    void mincut(vector<int>& ans) {
        bfs();
        for(int i = 0; i < edges.size(); i++) {
            Edge& e = edges[i];
            if(!vis[e.from] && vis[e.to] && e.cap > 0) ans.push_back(i);
        }
    }
    void print() {
        printf("Graph:\n");
        for(int i = 0; i < edges.size(); i++)
            printf("%d->%d, %d, %d\n", edges[i].from, edges[i].to , edges[i].cap, edges[i].flow);
    }
} isap;

int n, m;


struct xxx
{
    int u,v;
}eee[3000*2];
int known_num;
int isbiao[600];
int biao[600];
int marks[600];
int ans[600];
int mp[600][600];

void init()
{
    scanf("%d%d", &n, &m);
    clr(mp,0);
    for (int i = 0; i != m; ++ i)
    {
        scanf("%d%d", &eee[i].u, &eee[i].v);
        mp[eee[i].u][eee[i].v]=1;
        mp[eee[i].v][eee[i].u]=1;
    }
    scanf("%d", &known_num);
    clr(isbiao, 0);
    clr(ans, 0);
    for (int i = 1; i <= known_num; ++ i)
    {
        int a,b;
        scanf("%d%d", &a, &b);
        isbiao[a]=1;
        biao[a]=b;
    }
}


void cal()
{
    isap.init(n + 5);
    for (int i = 0; i <=n; ++ i)
        for (int j = i+1; j <=n;++j)
        {
            if (mp[i][j])
            {
                isap.add_edge(i, j, 1);
                isap.add_edge(j, i, 1);
            }
        }
    for (int i = 1; i <= n; ++ i)
    {
        if (!isbiao[i]) continue;
        if (marks[i])
        {
            isap.add_edge(0, i, INF);
        }else
        {
            isap.add_edge(i, n + 1, INF);
        }
    }
    isap.maxflow(0, n + 1);

}

void doit()
{
    clr(ans, 0);
    for (int i = 1; i <= 31; ++ i)
    {
        for (int j = 1; j <= n; ++ j)
        {
            ans[j]<<=1;
            if (!isbiao[j]) continue;
            marks[j] = (biao[j]>>(31-i))&1;
        }
        cal();
        isap.doit(ans);
    }
    for (int i = 1; i <= n; ++ i)
        printf("%d\n", ans[i]);
}


int main()
{
    int T;
    scanf("%d", &T);
    while (T--)
    {
        init();
        doit();
    }
    return 0;
}

例题三：NOI 2006 Day 2 最大获利(Profit)

题目大意:

• 紫比利的公司 得到了 一共 n个可以作为通讯信号中转站的地址。由于这些 地址的理位置 差异 ，在不同的地方建造通讯中转站所需要投入成本也 是不一样的，所幸在前期调查之后 这些 都是已知数据：建立 第 i个通讯中 转站需要 成本 pi。
• 另外公司调查得出了所有期望中的 用户群 ，一共 m个。第 i个用户 群的用户 会使用 中转站 ai和中转站 bi进行 通讯，公司 获益 ci。紫比利 公司 可以有 选择地建立一些中转站（其成本之和为总），用户提供服务并获得 收益（ 收益之和为总） 。
• 求出一个建造方案，使得公司的净获利最大。（ 净获利 =总 收益－成本 ）
• N≤5000，M≤50000，0≤ci≤100，0≤pi≤100

分析 :
在讲题目之前请先搞懂两个概念：

①最大权闭合子图：

• 定义一个有向图 G=(V,e)的闭合子图是该有向图的一个点集 ，且的所有出边都还指向该点集。即闭合子图内任意点的后继也一定在 闭合子图 中。
• 更形式化地说， 闭合子图是这样的一个点集 V′∈V，满足对于 ∀(u,v)∈E， 若有 u∈V′成立，必有v∈V′成立。
• 按照上面的定义， 闭合子图是允许超过一个连通块的。
• 给每个点 v分配一个点权 w_v（任意实数，可正负）。 最大权闭合子图 ， 是一个点权之和最大的闭合图，即化 Σv∈V′W_v。
• 在下图 中的网络 有9个闭合图（含空集） ：∅,{3,4,5},{4,5},{5},{2,4,5},{2,5},{2,3,4,5},{1,2,4,5},{1,2,3,4,5}，其中 有最大权和的闭合图 是{3,4,5}，权和为4。

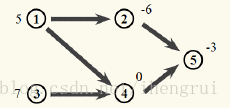
• 最大权闭合子图可以用最小割模型来解决， S集表示选入闭合子图中的点， T集表示不选入闭合子图中的点。
• 下面给出具体的将原问题图 G转化为网络 N=(VN,EN)的方法。
• 对于原图每一条有向边 (u,v)∈E，连一条容量为 ，连一条容量为 ，连一条容量为 ∞的有向边 的有向边 (u,v)。
• 对于原图中每一个正权点 v(wv>0)，连一条容量为 ，连一条容量为 ，连一条容量为 wv的有向边 的有向边 (s,v)。
• 对于原图中每一个负权点 v(wv<0)，连一条容量为 连一条容量为 −wv的有向边 的有向边 (v,t)。
• 最后的答案就是:

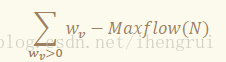
接下来我们来证一下这个式子的正确性。

• 首先，如果一个点v被选入了S集中，那么所有它连出去的点都要被选中S集中，因为它们之间连的边的容量是正无穷，这些边是绝对不会被割掉的。这和闭合子图的定义相同。
• 而如果一个负权点v被选到了S集中（即被包含在闭合子图中，它对最终答案贡献就会从原来的假设的0变为实际的−wv），那么就必须把它连到t的边割掉，产生−wv的贡献。
• 类似的，如果一个正权点v被选到了T集中，那么它（即不被包含在闭合子图中，它对最终答案贡献就会从原来的假设的wv变为实际的0），那么就必须把s连到它的边割掉，同样产生−wv的贡献。

这样就轻易地证完了。

回到题目：

• 题目中说在满足了第 i个用户群之后，便可以得到收益 ci，然而需要一个 必要条件：建立中转站 ai和 bi，同时要花费相应的用。
• 我们稍微分析一下就可以把它转化为个有向图模型：每用户群 i看 作一个点，权为 ci。再把每一个中转站 j看作一个点，权为 −pj。然 后从每个用户群向它需要的两中转站连边。
• 求一下这个图的最大权闭合子，就可以完成本题。
• 时间复杂度为 O(Max(flow(n+m),n+m))。
• 然而其实还有一种解法。
• 我们可以把它转化为带边权点的类最大密度子图

那么，什么是最大密度子图？

②最大密度子图：

定义一个无向图 G=(V,E)的密度为该图边数 |E|与该图的点数 V的比值。
给出一个无向图 ，其具有最大密度的子G′=(V′,E′)称为最大密度子图， 即最大化 D′=|E′|/|V′|。
更形式化地说，我们的目标就是:

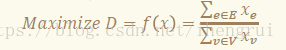
• 其中 x_e,x_v∈{0,1}，表示每个点或者条边是否在子图 G’中。
• 这是一个 0-1分数规划的模型。我们接下来应该二一个答案 g，并且计算

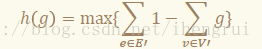
再根据h(g)的正负性决定继续二分的范围。

我们稍微改变一下ℎ(g)的值：

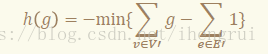
即我们的目标是:

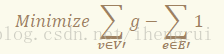
因为要让选的边尽量多，所以我们肯定选择V′的导出子图。V’的导出子图中的边数可以被计算为:

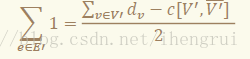
所以：

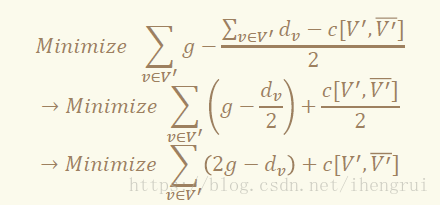
• 于是我们从 s向每个点 v连权值为 U的边，从每个点 v向t连权值为 U+2g−dv的边， 其中 U表示一个足够大的数使得边权为非 表示一个足够大的数使得边权为非 负；对于 负；对于 原图中的每条边 原图中的每条边 (u,v)∈E，连 两条容量为 1的有向边 (u,v)和(v,u)。
• 然后跑最小割，答案再减去 U·n就行。
• 证明非常简单：如果我们要选一个点 v的话，就要付出 的话，就要付出 的话，就要付出 2g−dv的代价；两个端 的代价；两个端 的代价；两个端 点在不同集合里的边必须要全部割掉，总代价是 点在不同集合里的边必须要全部割掉，总代价是 点在不同集合里的边必须要全部割掉，总代价是 c(V′,V′)。

③带边权点最大密度子图：

如果要算有边权和点的最大密度子图呢？即除了每条一个非负之外，每个点 v还有一个可正负的点权 p_v。
定义点边均带权的无向图密度为该和 加上Σv∈Vp_w+Σe∈Ew_e与该图的点数 |V|的比值，即

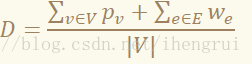
我们同样使用 0-1分数规划，二答案 g，目标就变成了选出一个 G的子图 G’=(V’,E’)，且最大化

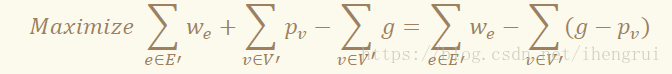
• 我们重新定义 d_u，改为与 u关联的所有边权值和，即 d_u=Σ(u,v)∈EW_e。
• 再将所有边 e在网络中对应的边容量从 1改为 W_e。
• 最后再将任意点 v到t的容量改为 c(v,t)=U+2g−p_v−d_c，s连到t的边 的容量保持 U不变。
• 同样直接跑最小割，答案减去 U·n就行。

最终分析：
• 将用户群看成边 ，中转站点问题就可以换为：选出一些e使其 “满足”，可 得到收益 w_e；选出一些 点v进行 “建设” ，花 去费用 p_w。
• 这些选出的点组成 V’，选出的边组成 E’，解题目标便转化为

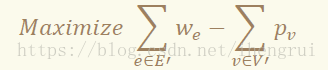
• 限制 条件是如果一边被选，那么它的两个端点也要这和最大密度 子图是相同的。
• 类比一下带权最大密度子图的优化目标：

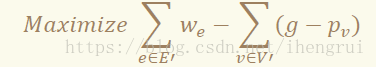
• 我们把其中的 (g−p_w)用本题中的 p_v代入，便可在 O(MaxFlow(n,n+m))的时间内解决本题。
• 至此，本题解答完毕（贴下代码）。

#include<set>
#include<map>
#include<cmath>
#include<string>
#include<cstdio>
#include<vector>
#include<cctype>
#include<cstdlib>
#include<sstream>
#include<cstring>
#include<iostream>
#include<algorithm>

#define For(i,x,y) for (int i=x;i<y;i++)
#define pb push_back
#define mp make_pair
#define fir first
#define sec second

#define dprintf(...) fprintf(stderr,__VA_ARGS__)
using namespace std;

int IN()
{
    int c,f,x;
    while (!isdigit(c=getchar())&&c!='-');c=='-'?(f=1,x=0):(f=0,x=c-'0');
    while (isdigit(c=getchar())) x=(x<<1)+(x<<3)+c-'0';return !f?x:-x;
}

typedef long long ll;
typedef double Db;
typedef pair<int,int> pii;

const int N=5000+19,M=5000000;
const ll oo=1ll<<60;
typedef int one[N];
struct Edge {int y,f,nxt;} E[M];
one Last,Q,Dis,sum,p,cur;
int n,m,cnt,S,T,U,x,y,z;
ll Ans;

void Add_Edge(int x,int y,int f)
{
    E[cnt]=(Edge){y,f,Last[x]};Last[x]=cnt++;
}
bool BFS()
{
    memset(Dis,-1,sizeof(Dis));Dis[S]=0;
    int f=1,w=0;Q[1]=S;
    while (f>w)
    {
        int x=Q[++w];
        for (int i=Last[x],y;~i;i=E[i].nxt)
            if (E[i].f&&Dis[y=E[i].y]==-1) Dis[y]=Dis[x]+1,Q[++f]=y;
    }
    return Dis[T]!=-1;
}
ll Dinic(int x,ll Flow)
{
    if (x==T||!Flow) return Flow;
    ll res=0;
    for (int i=cur[x],y;~i;i=E[i].nxt)
        if (E[i].f&&Dis[y=E[i].y]==Dis[x]+1)
        {
            ll tmp=Dinic(y,min(1ll*E[i].f,Flow));
            E[i].f-=tmp,E[i^1].f+=tmp,Flow-=tmp,res+=tmp;
            if (E[i].f) cur[x]=i;
            if (!Flow) return res;
        }
    if (!res) Dis[x]=-1;
    return res;
}

int main()
{
    memset(Last,-1,sizeof(Last));
    n=IN(),m=IN();
    For(i,1,n+1) p[i]=IN();
    For(i,0,m)
    {
        x=IN(),y=IN(),z=IN();
        sum[x]+=z,sum[y]+=z;
        Add_Edge(x,y,z),Add_Edge(y,x,z);
    }
    For(i,1,n+1) U=max(U,sum[i]);
    S=n+1,T=S+1;
    For(i,1,n+1)
    {
        Add_Edge(S,i,U),Add_Edge(i,S,0);
        Add_Edge(i,T,2*p[i]-sum[i]+U),Add_Edge(T,i,0);
    }
    while (BFS()){
        For(i,1,T+1) cur[i]=Last[i];
        Ans+=Dinic(S,oo);
    }
    printf("%lld\n",(1ll*U*n-Ans)/2);
}

例题大概就酱紫吧，以后有空再更。
我超蒻的。

其他可以联系我的QQ：858366568.