基于多项式承诺的可验证计算

基于多项式承诺的云计算安全公开可验证计算

摘要

计算外包是一种可为用户提供的关键云服务。对于使用轻量级设备的用户而言，利用云来处理复杂计算至关重要。然而，由于经济原因，云可能无法正确执行计算任务。本文提出了一种基于多项式承诺的云计算中安全的公开可验证计算方案。得益于多项式承诺的公钥去承诺特性，我们的方案能够为计算结果提供公开可验证性。安全分析表明，提出的方案是正确的，并能支持公开可验证性。对比和仿真结果显示，与以往方案相比，我们的方案具有较低的计算成本。

关键词 ：计算外包 · Verifiable计算 · 多项式承诺 · Public可验证性

1 引言

云计算是一种基于互联网的技术，随着计算机技术的发展而发展[3,20]。云由许多分布式服务器组成，这些服务器可以提供各种消费者服务[8,24,36]，例如多媒体娱乐、实时信息共享和远程医疗[10,11,16,19]。云消费者可以通过互联网随时随地享受云服务[5,17,21,30,33]，云服务器由云服务提供商（CSP）管理[20,22]。客户端必须按使用量付费[12,28]。尽管使用云并非免费，但与传统的存储和计算设备相比，云的使用费用并不昂贵。根据亚马逊网站上的最新价格，通用固态硬盘（SSD）的价格为每GB 0.10美元¹。更重要的是，利用云来存储数据和执行计算可以减少硬件和软件投资[7,14,23,25,29,35]，这为个人、公司和组织带来了巨大的经济效益。

随着互联网和云计算的发展，产生了大量基于云的远程服务。计算外包是一种重要的云服务。资源有限的用户可以委托云为其执行复杂计算[4,6,14,32,37,38]。许多领域依赖云基于存储的数据执行计算[15,18]。例如，气象局利用过去多年的降雨、降雪或灾害性气候数据，推断下一年各季节出现相应异常天气的概率。医生利用云评估患者的疾病数据，并分析常见疾病的季节性。

云计算的特殊性决定了计算外包方案的设计面临诸多安全问题[9,27,31]。一方面，云可能攻击存储的数据，导致外包计算产生错误的输出；另一方面，云可能为了节省存储资源而丢弃不常使用的数据。当某个用户希望使用相应数据进行计算时，云会随机选择一个结果或使用之前的计算结果来欺骗用户。因此，设计具有可验证性的计算外包方案是必要的[2,26]。近年来，许多研究人员致力于可验证计算的研究[18,34,37,38]。为了增强系统的安全性，一些研究人员设计了具有公开可验证性的可验证计算方案[1,26,32]，这在实际的计算外包系统中更具实用性。然而，现有的可验证方案主要集中在同态加密的研究上，给系统带来了巨大的计算成本。此外，用户还需要参与验证过程，影响了系统的安全性和效率。因此，有必要为云计算设计一种新型的、高效的安全公开可验证计算系统。

在本文中，通过利用多项式承诺，我们提出了一种适用于云计算的安全公开可验证计算方案。本文的主要贡献如下：
– 由于利用了多项式承诺，提出的方案中云的计算结果可由可信机构（TA）代表用户进行安全验证。
– 提出的方案可以为计算结果提供公开可验证性。换句话说，任何实体都可以委托TA使用公钥来验证计算结果的正确性。
– 输入和计算多项式与系统效率无关；数据大小和计算多项式次数不会给系统带来额外负担。

本文的其余部分组织如下。第2节介绍与提出的方案相关的研究工作。第3节列出提出的方案中使用的一些预备知识。第4节描述提出的方案的系统模型、威胁模型以及设计目标。第5节详细介绍了提出的方案，第6节提供了安全性和性能分析。本文的结论在第7节给出。

2 相关工作

在可验证计算研究中，已提出了许多相关方案[18,34,37,38]。在[37]中，周等提出了一种云计算中指数运算的安全且可验证外包方案。在外包阶段，该方案在本地仅需进行少量模乘法运算，效率非常高，因此可在轻量级移动设备上执行。此外，周等提出的方案为用户提供了一种验证机制，以检查计算结果的有效性。为解决隐私泄露问题，卓等在[38]中提出了一种大数据环境下的隐私保护的可验证集合操作。在卓等的方案中，用户可以在保护隐私的前提下验证操作结果的正确性。同时，卓等扩展了其方案以支持数据预处理和批量验证，大大降低了系统的计算成本。在[18]中，刘等提出了一种针对公开数据的高效隐私保护外包计算方案，允许用户将对公开数据的复杂计算外包给云。需要注意的是，该方案基于可切换同态加密设计，在计算外包过程中能够保护计算函数及其输出的隐私。为解决云审计中的密钥更新问题，余等在[34]中利用可验证计算外包设计了具有密钥更新可验证外包功能的云存储审计方案，将密钥更新任务安全地外包给第三方审计员（TPA）。TPA中的私钥以加密形式存储，因此当用户需要上传数据到云时，必须先下载加密密钥并解密它。此外，用户可以验证TPA是否已更新私钥。

为了满足实际需求并增强系统安全，一些研究人员提出了具有公开可验证性的外包计算方案[1,26,32]。Alderman et al. 在[1]中提出了一种可撤销的公开可验证计算方案，该方案能够将作弊服务器从系统中撤销。为了处理密钥生成和密钥分发，Alderman et al. 在其方案中引入了密钥分发中心（KDC）。该KDC可以验证来自云的结果；此外，KDC 是一个可信实体，可以在系统中执行服务器撤销。

在[32]，Wang等人提出了一种安全协作的公开可验证计算方案，以增强计算外包系统的灵活性。通过利用代数运算结构，Wang等人的方案能够基于先前的函数以及私有云的函数构造目标函数。此外，该方案允许私有云验证目标函数的完整性，并允许用户检查结果的正确性。在[26]，Song等人提出了一种基于同态可验证计算标签结构的多项式求值验证方案，该方案可用于具有公开可验证性的多数据源场景。此外，该方案效率更高，且客户端的计算开销与输入和多项式规模无关，非常适合移动环境。

3 预备知识

本节介绍提出方案的预备知识。首先，介绍了用于构建提出方案的双线性对。然后，简要介绍了多项式承诺技术。

3.1 双线性对

设 $G_1$ 和 $G_2$ 是两个素数阶的乘法群 $q$。双线性对可以表示为 $\hat{e}: G_1 \times G_1 \rightarrow G_2$。假设 $P, Q \in G_1$, $x, y \in \mathbb{Z}_q^ $ 和 $G$ 是 $G_1$ 的生成元。双线性对的三个性质如下所示：
– 双线性 : $\hat{e}(P^x, Q^y) = \hat{e}(P, Q)^{xy}$。
– 非退化 : $\hat{e}(G, G) \neq 1$。
– 可计算 *: $\hat{e}(P, Q)$ 可通过算法计算。

3.2 多项式承诺

多项式承诺技术[13]可用于可验证方案的设计。此处简要介绍多项式承诺的过程如下：
– 设置 (1θ, t)：该过程生成私钥和公钥，假设由系统中的可信实体执行此过程。其中，t为多项式次数。
– 承诺 (PK, φ(x))：该过程具有两个功能。第一，计算多项式 φ(x) 的承诺；第二，为系统生成一个去承诺密钥 dk。
– 打开 (PK, C, dk)：该过程使用 dk 对承诺 C 进行去承诺。
– 验证多项式 (PK, C, φ(x), i, dk)：验证者根据 C、PK、φ(x)、i和 dk 验证承诺的正确性。
– 验证求值 (PK, C, i, φ(x), wi)：该过程验证 φ(x) 是否为承诺在 C 中的多项式的求值结果。

4 问题陈述

本节对系统模型和威胁模型进行了形式化描述，并介绍了提出方案的设计目标。

4.1 系统模型

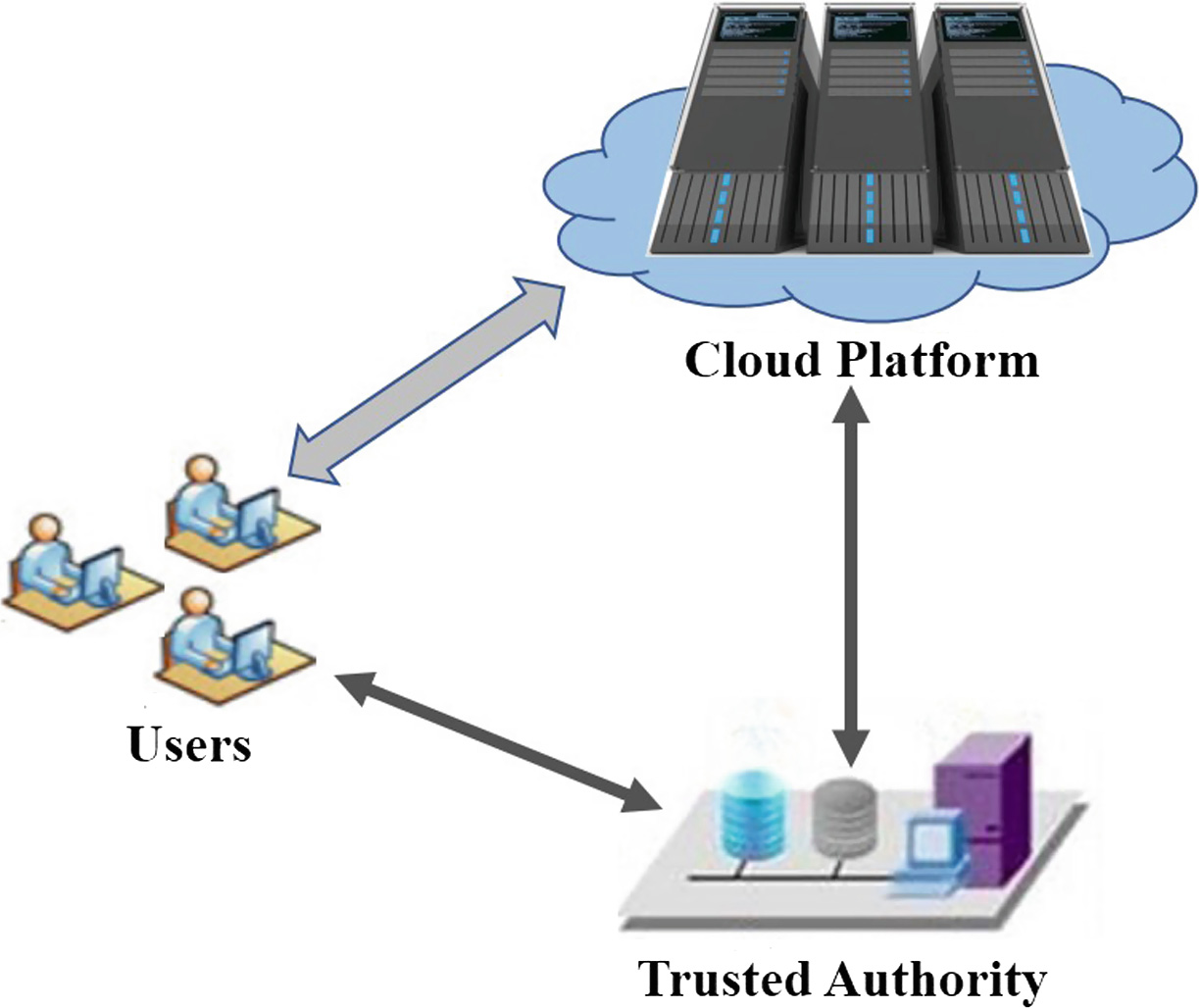
我们的可验证计算系统包含三种实体，分别是可信方（TA）、用户和云平台。系统模型如图1所示。以下是对这些实体的详细介绍：
– 可信机构（TA） ：TA 是系统中完全可信的实体。TA 的主要任务是协助用户验证来自云的计算结果。此外，TA 负责为系统生成多项式、安全参数和计算多项式。同时，TA 还可以代表用户验证计算结果的正确性。
– 用户 ：用户是通过互联网使用云服务的云消费者。在提出的方案中，用户将其数据上传至云服务器，并将计算任务委托给云。用户以按使用付费的方式使用计算服务。需要注意的是，用户的计算能力和存储资源有限。
– 云平台 ：云平台由许多分布式服务器组成，这些服务器通过网络相互连接。云平台为云用户提供各种服务。与 TA 相比，云平台是半可信的。云平台具有强大的计算能力，能够利用相应的数据和计算多项式为用户执行计算任务。

4.2 威胁模型

在所提出的系统中，云负责存储用户数据并帮助用户处理数据。然而，云是好奇但诚实的。此外，一些被腐蚀的用户或外部攻击者可能会与云合谋攻击系统[26]。本文考虑了以下三种潜在威胁。
– 数据损坏 ：云服务器可能由于经济原因导致数据损坏。此外，外部攻击者可能会破坏或篡改云中的数据。除非损坏数据的出现影响云服务提供商的利益，否则云并不关心存储数据的正确性。云中的损坏数据可能导致错误的计算结果。
– 错误输出 ：错误或不完整输入可能导致错误输出。云服务器可能使用先前的计算结果或其他随机选择的参数作为输出来欺骗用户。
– 伪造攻击 ：云服务器、被腐蚀的用户或其他外部攻击者可能伪造计算结果或验证请求提交给可信方，以试图通过验证。伪造攻击的威胁可能影响系统中其他未被腐蚀的云服务器和用户的可信性。

4.3 设计目标

在本文中，我们提出了一种用于云计算的可验证计算方案。我们的方案的设计目标如下：
– 正确性 ：在上述安全威胁下，可信方（TA）能够验证计算结果的正确性。换句话说，无论当前计算结果是否正确，可信方（TA）都能够验证该结果。
– 公开可验证性 ：可验证计算方案应支持公开可验证性。即，系统中的任何用户或实体都可以请求可信方（TA）使用公共参数或密钥来验证云中计算结果的正确性。
– 效率 ：可验证计算方案可以以较低的计算成本执行。需要注意的是，大多数计算任务被委托给云和可信方（TA）。在用户的数据被外包到云之后，用户端仅需生成必要的安全参数和密钥。此外，计算多项式和系统输入与系统效率无关。

5 提出的方案

在本节中，将详细描述提出的方案。该方案的流程如图2所示。以下是对我们的方案的详细说明：

(1) 用户依赖云来存储和计算他们的数据。通常情况下，数据由用户加密后上传到云。假设一个用户 $U_i$ 将其数据 $M$ 上传到云。$M$ 的数据被划分为 $n$ 个数据块，对应的数据块索引为 $I_1, I_2, \cdots, I_n$。

(2) 可信方定义了一个多项式 $F(x) = \sum_{i,j=1}^{n} c_i \cdot x^{e_j}$，用于与用户的数据一起执行计算。注意，$c_i$ 和 $e_j$ 是由用户定义的常数。$F(x)$ 的多项式被发送到云。同时，可信方生成一个多项式 $\alpha(x) \in \mathbb{Z}_q[x]$ 用于进一步计算结果验证，其中 $q$ 是一个大素数阶。假设 $\alpha(x)$ 的次数为 $t$。相应地，$\alpha(x)$ 的系数可表示为 $\alpha_i$，其中 $0 \leq i \leq t$。

(3) 如果 $U_i$ 想要计算 $m_i$，他/她需要根据其计算需求定义常数 $c_i$ 和 $e_j$。同时，$U_i$ 需要生成一个包含数据块相应索引信息的计算请求。这些常数和计算请求被发送到云。云在接收到计算请求后，使用计算多项式 $F(x)$ 来计算 $m_i$。假设 $m_i$ 的计算结果为 $R_i$，则将计算结果 $R_i$ 发送给 $U_i$ 和可信方。可信方在接收到 $R_i$ 后，基于数据块信息和 $\alpha(\lambda_i) = R_i$ 生成一个安全参数 $\lambda_i \in \mathbb{Z}_q$。该参数 $\lambda_i$ 由可信方本地存储，用于进一步计算结果验证。

(4) 如果 $U_i$ 想要验证计算结果 $R_i$ 的正确性，则需要向可信方TA发起请求以建立验证机制。假设 $U_i$ 从 $\mathbb{Z} q^*$ 中随机选择 $r_i$，并令 ${\hat{e}, G_1, G_2, P, Pr_i}$ 作为计算结果验证的公钥。然后，$U_i$ 根据计算结果 $R_i$ 生成验证请求 $Req {R_i}$，并通过安全信道将 $Req_{R_i}$ 和 $r_i$ 发送给可信方。

(5) 当可信方收到来自 $U_i$ 的验证请求时，可信方选择一个多项式 $\beta(x) \in \mathbb{Z} q[x]$，并计算用于验证的多项式承诺 $C = P^{\alpha(r_i)} \cdot Q^{\beta(r_i)}$，其中 $C \in G_1$。然后，可信方为 $\lambda_i$ 计算两个多项式 $A {\lambda_i}(x) = \frac{\alpha(x)-\alpha(\lambda_i)}{x-\lambda_i}$ 和 $B_{\lambda_i}(x) = \frac{\beta(x)-\beta(\lambda_i)}{x-\lambda_i}$。同时，可信方基于上述两个多项式，针对参数 $\lambda_i$ 计算两个辅助多项式承诺 $C1_{\lambda_i} = P^{\alpha(\lambda_i)} \cdot Q^{\beta(\lambda_i)}$ 和 $C2_{\lambda_i} = P^{A_{\lambda_i}(r_i)} \cdot Q^{B_{\lambda_i}(r_i)}$。

(6) 在验证阶段，$U_i$ 可以利用公钥和承诺来验证计算结果 $R_i$ 的正确性。验证方程如下：
$$
\hat{e}(C,P) \stackrel{?}{=} \hat{e}(C1_{\lambda_i},P)\cdot \hat{e}(C2_{\lambda_i},Pr_i /P^{\lambda_i})
$$
如果上述验证方程的左边等于右边，则计算结果 $R_i$ 是正确的。否则，云服务器或相应数据已被破坏。

6 安全分析和性能分析

本节介绍了安全分析和性能分析。在安全分析中，证明了提出方案的正确性和公开可验证性。在性能分析中，给出了我们方案的模拟及其与先前方案的比较。

6.1 安全分析

定理1. 提出的方案在验证计算结果的正确性方面是正确的。

证明. 根据第5节中该方案的描述，$U_i$ 可以确定若验证方程成立，则此方案的验证是正确的。验证方程的右边可计算为：
$$
\hat{e}(C1_{\lambda_i},P) \cdot \hat{e}(C2_{\lambda_i},Pr_i /P^{\lambda_i}) = \hat{e}(P^{\alpha(\lambda_i)}Q^{\beta(\lambda_i)},P) \cdot \hat{e}(PA_{\lambda_i}(r_i)QB_{\lambda_i}(r_i),P^{r_i -\lambda_i})
$$
假设 $Q = P^\kappa$，我们可以得到：
$$
\hat{e}(P^{\alpha(\lambda_i) +\kappa\cdot\beta(\lambda_i)},P) \cdot \hat{e}(P^{A_{\lambda_i}(r_i) +\kappa\cdot B_{\lambda_i}(r_i)},P^{r_i -\lambda_i}) = \hat{e}(P,P)^{(\alpha(\lambda_i) +\kappa\cdot\beta(\lambda_i)) +(A_{\lambda_i}(r_i) +\kappa\cdot B_{\lambda_i}(r_i))\cdot(r_i -\lambda_i)}
$$
注意 $A_{\lambda_i}(x)$ 和 $B_{\lambda_i}(x)$ 的构造使得：
$$
(A_{\lambda_i}(\lambda_i)+ \kappa \cdot B_{\lambda_i}(\lambda_i))\cdot(r_i - \lambda_i) = (\frac{\alpha(r_i) -\alpha(\lambda_i)}{r_i -\lambda_i} + \kappa \cdot \frac{\beta(r_i) -\beta(\lambda_i)}{r_i -\lambda_i})\cdot(r_i - \lambda_i) = \alpha(r_i) - \alpha(\lambda_i)+ \kappa \cdot(\beta(r_i)- \beta(\lambda_i))
$$
进而可得：
$$
(\alpha(\lambda_i)+ \kappa \cdot \beta(\lambda_i))+(A_{\lambda_i}(\lambda_i)+ \kappa \cdot B_{\lambda_i}(\lambda_i))\cdot(r_i - \lambda_i) = \alpha(r_i)+ \kappa \cdot \beta(r_i)
$$
因此验证方程右侧的结果为：
$$
\hat{e}(P,P)^{\alpha(r_i)+\kappa\cdot\beta(r_i)} = \hat{e}(P^{\alpha(r_i)}Q^{\beta(r_i)},P) = \hat{e}(C,P)
$$
即验证方程成立。因此，本文的验证过程是正确的。

定理2. 提出的方案支持对计算结果的公开可验证性。

证明. 在计算结果验证阶段，$U_i$ 可以使用公钥 $P$、$Pr_i$ 以及承诺 $C$、$C1_{\lambda_i}$ 和 $C2_{\lambda_i}$ 来验证计算结果 $R_i$ 的正确性。也就是说，任何实体都可以利用公钥委托可信方TA验证计算结果的正确性。因此，提出的方案支持公开可验证性。

6.2 性能分析

本小节分析了提出方案的性能。我们将我们的方案与之前提出的两种方案进行了比较[18,26]，比较内容包括对比分析和仿真分析。

(1) 对比分析

为了便于性能比较，我们使用符号 $P$、$M$、$E$、$A$ 和 $H$ 分别表示配对、乘法、指数运算、加法和哈希操作。比较结果如表1所示。从比较结果可以看出，我们的方案的计算成本为 $3P + (6+n)E + (10+n)M + (4+n)A$。注意，符号 $n$ 是计算多项式的次数。表1表明，当 $n$ 足够大时，我们的方案与宋等人的方案在指数运算、乘法和加法上的计算成本相对接近。然而，宋等人方案中的配对成本高于我们的方案。更重要的是，宋等人的方案包含哈希操作，这大大增加了系统的计算成本，因此我们的方案比他们的方案更高效。与刘等人方案的计算成本[18]相比，显然我们的方案在指数运算、乘法和加法上的成本更低。在实际的可验证计算系统中，由于 $n$ 非常大，我们方案中的配对计算成本可以忽略不计。

方案	计算成本	公开可验证性
宋 et al的方案[26]	$4P + (7+n)E + 2H + (4+n)M + (7+n)A$	Y
刘 et al.的方案[18]	$(14+3n)E + (18+4n)M + (8+n)A$	N
我们的方案	$3P + (6+n)E + (10+n)M + (4+n)A$	Y

*P：配对； M：乘法； E：指数运算； A：加法； H：哈希； n：计算多项式的次数

这表明刘等人的方案比我们的方案具有更高的计算成本。此外，表中还列出了两种方案以及我们的方案对公开可验证性的支持情况。从比较结果可以看出，与宋等人和刘等人的方案相比，我们的方案能够实现公开可验证性且计算成本更低。

(2) 仿真分析

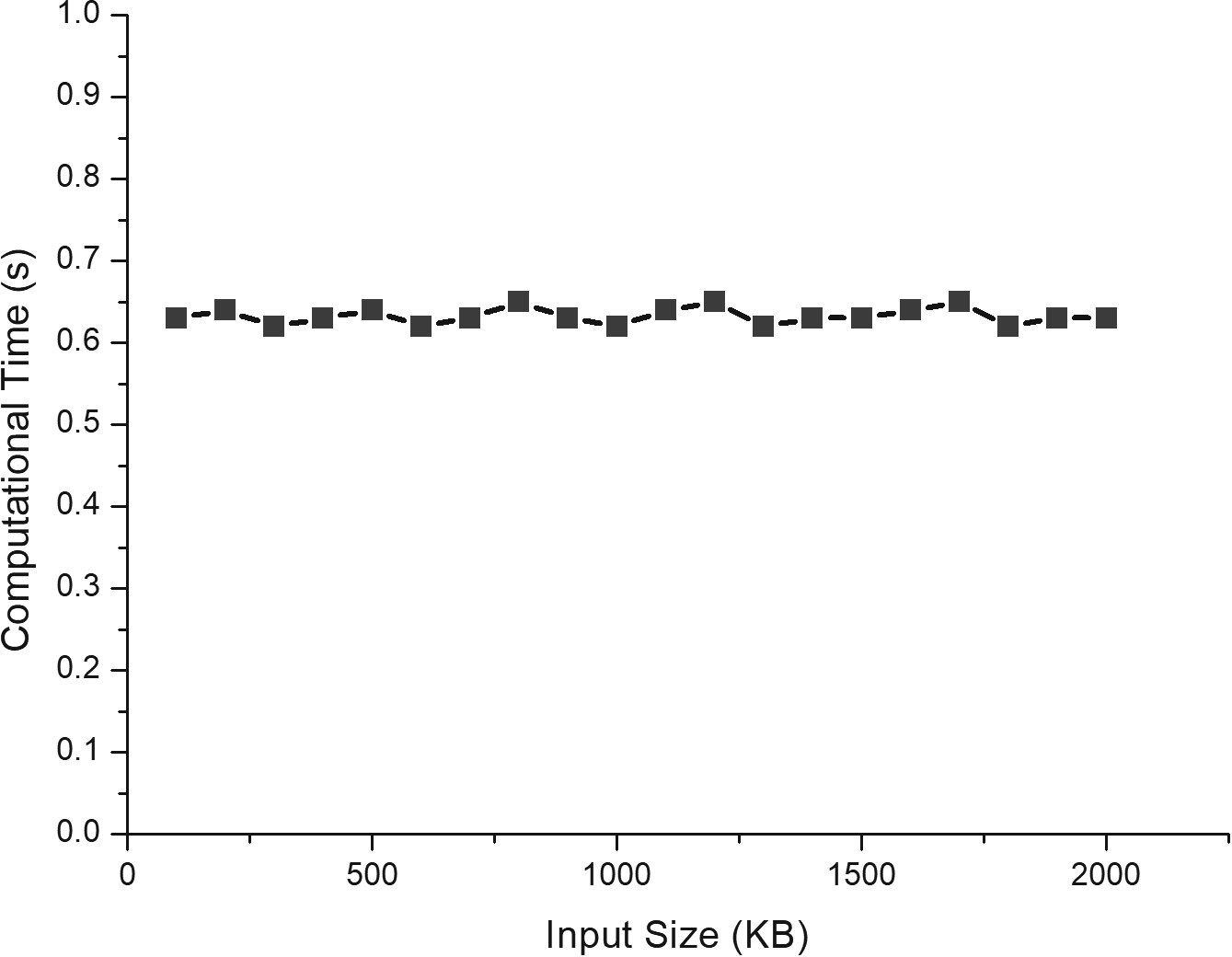
提出的方案和两个相似的方案[18,26]在由GMP库（GMP-6.1.2）和PBC库（pbc-0.5.14）配置的实验平台上进行了仿真。实验平台构建于配备8 GB内存和2.6 GHz CPU的Linux系统上。为了在实验平台上模拟我们的方案和两个相似的方案，我们将计算多项式的次数设置为100。由于计算任务由云使用计算多项式执行，输入规模不会影响系统效率。我们使用不同的数据大小作为计算多项式的输入 $F(x)$。不同数据大小下计算多项式的仿真结果如图3所示，从中我们可以确定，不同数据大小下的计算时间差异非常小。也就是说，当系统输入不同大小的数据时，计算时间相对恒定。因此，不同输入规模下计算多项式的仿真结果满足效率设计目标。

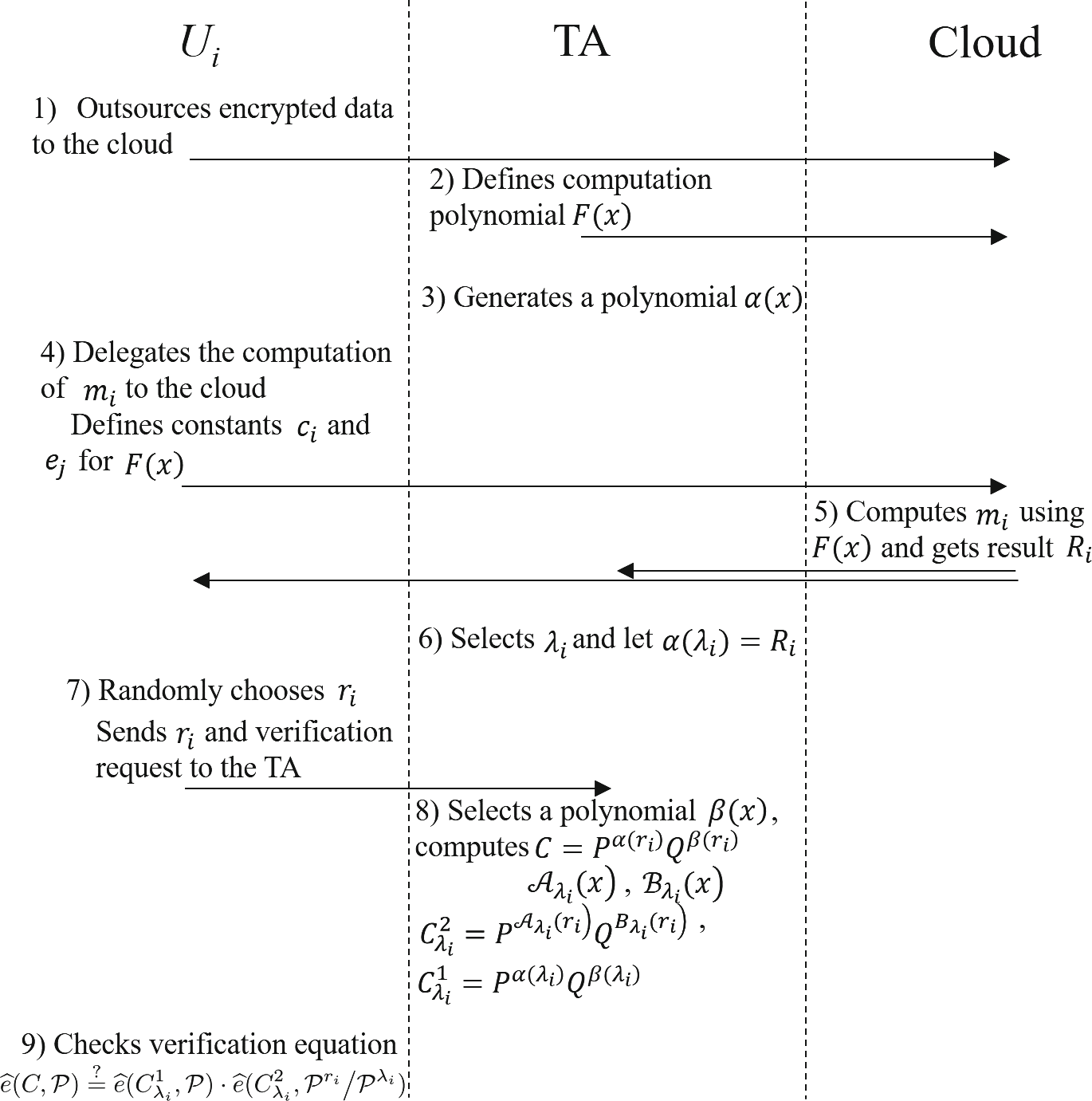
图4显示了提出的方案和两个相似的方案的仿真结果[18,26]。注意，图4的横轴是计算次数。从图4可以看出，我们的方案和两个相似的方案的计算时间随着计算次数的增加而线性增加。然而，对于相同的计算次数，我们的方案的计算时间始终小于两个相似的方案。因此，我们的方案比刘等[18]和宋等[26]更高效。

7 结论

本文中，我们提出了一种基于云计算中多项式承诺的安全公开可验证计算方案。在我们的方案中，公钥可用于验证来自云的计算结果。换句话说，我们的方案支持公开可验证性。正确性和公开可验证性在安全分析中得到证明，符合提出方案的设计目标。在性能分析中，我们将我们的方案与刘等[18]和宋等[26]的方案进行了比较。从比较结果可以确定，我们的方案比相似的方案更高效。此外，仿真结果表明，我们的方案确实使用了更少的计算时间与类似方案相比。因此，可以总结出我们的方案能够很好地用于云计算中的公开可验证计算。