DL-SLAM：直接2.5D激光雷达SLAM

原创于 2025-10-19 03:32:47 发布 · 1k 阅读

14 ·

CC 4.0 BY-SA版权

文章标签：

#SLAM # 激光雷达 # 2.5D高度图 # 回环检测

部署运行你感兴趣的模型镜像

DL‐SLAM：用于自动驾驶的直接2.5D激光雷达SLAM

摘要

在无GNSS城市区域中精确定位车辆对于自动驾驶至关重要。基于占用栅格的2D激光雷达SLAM方法难以良好地扩展到室外道路场景，而基于3D点云的激光雷达SLAM方法则面临巨大的计算和存储成本。针对室内外环境下的精确实时激光雷达SLAM，本文提出了一种直接2.5D高度图SLAM系统。该系统通过引入2.5D段特征以实现高效的回环检测，扩展了我们之前提出的DLO（直接2.5D激光雷达里程计）方法。我们在KITTI数据集上对所提出的SLAM方法进行了实验，结果表明其性能优于现有的激光雷达SLAM方法。

一、引言

同步定位与建图（SLAM）是自动驾驶的关键技术之一。尽管差分GNSS在城市外的开阔区域已证明其可行性，但自动驾驶车辆在GNSS信号受限的区域（如城市街道）仍需依赖基于自身观测的精确实时定位手段[1]。

近年来，视觉和激光雷达SLAM系统都得到了广泛研究[2]。由于具有高精度和主动感知能力，激光雷达传感器及基于激光雷达的SLAM方法在自动驾驶车辆应用中受到了广泛关注。基于占用栅格地图（OGM）的二维激光雷达SLAM方法是最早提出的SLAM系统之一[3]。许多基于占用栅格地图的系统，如GMapping[4],、HectorSLAM[5]和制图者[6]，已被应用于多种自动驾驶系统，并在室内环境中表现出良好性能。然而，基于二维占用栅格地图的SLAM方法依赖于周围障碍物（如墙壁）形成的特征模式，在室外场景中这种情况通常不成立，因为道路边界的两个占用栅格地图帧很难区分。

为了提升室外性能，SLAM系统中采用了三维信息，例如点云[7]和体素[8]。然而，这带来了密集计算用于三维空间中的点云配准或体素匹配的计算成本较高，使得这些方法在在线定位中开销较大。其他方法依赖于从点云中提取的三维特征[9][10]。这些特征由人造建筑和基础设施的尖锐几何结构形成，因此在室外场景中容易受到植被的影响。

在[11],中，2.5D高程图被用于实现快速且精确的帧间配准。利用高度信息显著提升了室外场景的表征能力，同时也能很好地扩展到室内场景。用于2.5D高程图配准的直接法相较于ICP和基于特征的方法表现出更高的效率。然而，由于直接匹配方法依赖于良好的初始参数，2.5D高程图无法高效地用于回环检测。

本文提出从2.5D高度图中提取段特征，并将基于2.5D段的回环检测集成到DLO中。该方法受到SegMatch[12],的启发，其中通过从点云分割中提取多种直方图为精确回环检测提供支持。我们进一步将分割简化为2.5维，在严格的时间约束下实现了类似的效果。

本文的主要贡献如下：
基于从2.5D高度图中提取的2.5D段进行快速回环检测。
通过引入回环检测和基于图的优化，DLO被扩展为一个实时SLAM系统。
在KITTI里程计数据集上进行了大量实验，结果表明DL‐SLAM优于DLO和LOAM。

II.相关工作

现有的激光雷达SLAM方法可以根据其不同的场景表示分为基于点云的、基于特征的和基于网格的方法。

在基于点云的SLAM方法中，采用了迭代最近点（ICP）[14]算法进行两帧之间的配准。该方法直接计算两个点云集之间的欧氏距离，并通过迭代评估最近点对来优化变换，导致计算成本较高。此外，由于该算法对其初始值非常敏感，容易陷入局部最优。

1由于官方的LOAM是闭源的，我们采用了其在 https://github.com/laboshinl/loamvelodyne上的流行实现。目前，SegMatch已被扩展为SegMap[13]，但集成系统尚未可用于比较。

在基于特征的SLAM方法中，以点、面和线的形式提取特征，以促进后续的匹配过程。此外，还提出了基于特征的LO方法用于高效[15]。该方法提取平面和角点特征以实现快速匹配，并在与惯性测量单元集成后，在各种场景中取得了良好的效果。然而，在以道路为主的自动驾驶场景中，这些特征可能较为稀疏。并且在没有惯性测量单元的情况下，LOAM容易发生漂移。

基于网格地图的SLAM可以进一步分为二维、三维和2.5维。由于基于二维的方法无法应用于许多开放的室外环境，本节将重点讨论基于三维和2.5维的方法。三维正态分布变换算法[16]为每个三维体素建立正态分布，并最大化两帧点云配准的似然性，但其效率无法保证。

在[11],中，采用2.5D高程图实现鲁棒的帧间配准。用于2.5D高程图配准的直接法相较于ICP和基于特征的方法表现出更高的效率，但该方法缺乏回环检测能力。

[17]使用从三维点云中提取的直方图测量值来匹配关键直方图，从而避免了大量的计算。[13]采用从三维体素中提取的段，通过随机森林方法和几何验证方法进行匹配检测。我们的方法受到上述两种方法的启发，采用了在2.5D高程图上的直方图测量值，以进一步提高回环检测的效率。

III.方法

所提出方法的流程如图1所示。在本节中，我们将分别描述基于2.5维段的直接2.5维前端和闭环。

示意图0

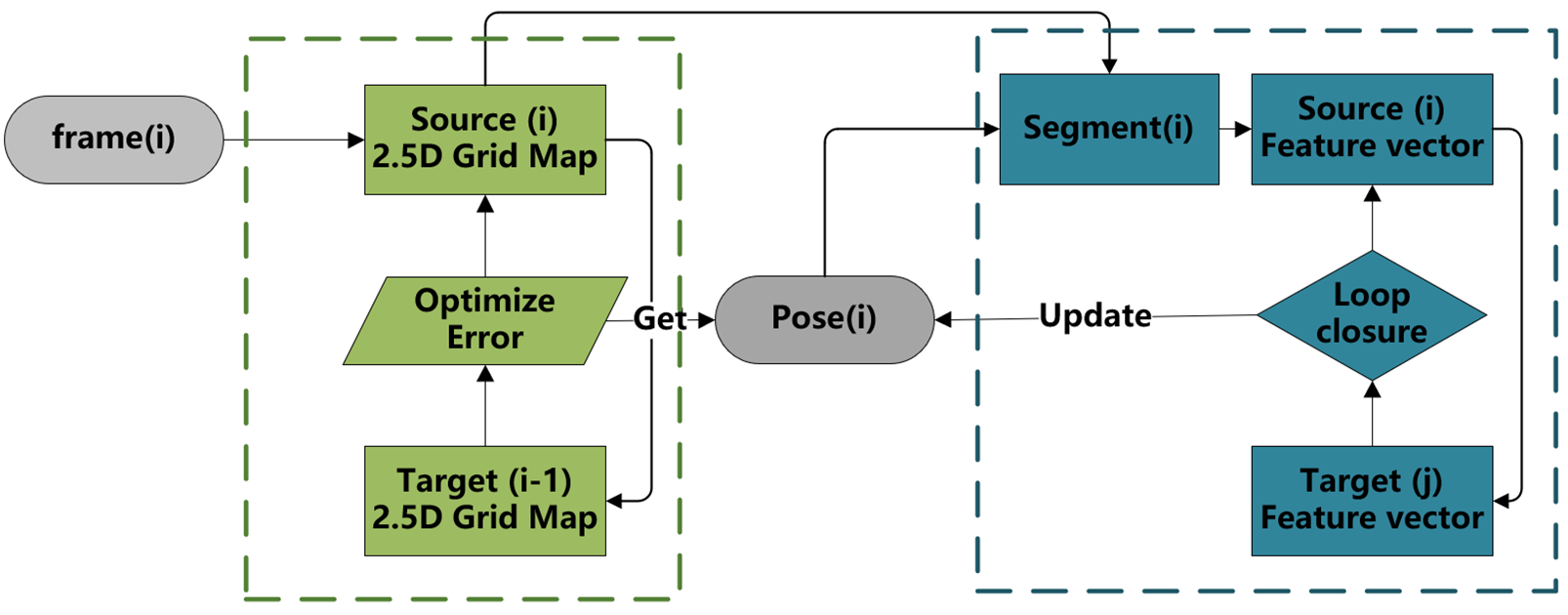
A.直接式2.5维前端

DLO[11]以2.5维高度图为操作基础，采用直接法通过优化两帧之间的高度差误差来估计位姿。

1)2.5维高度图：

多波束激光雷达传感器获取的点云数据能够高分辨率地准确且稳定地反映周围环境的几何结构。2.5维高度图保留了高度信息，并且与三维基于点云的方法相比降低了计算成本。

由(xi, yi, zi)表示的三维点云 pi被投影到2.5D高度图(ri, ci, hi)上，表示为 qi，使用的参数 fx, fy, cx和 cy分别代表栅格的分辨率和车辆中心位置。

$$
ri= xi ÷ fx+ cx \tag{1}
$$

$$
ci= yi ÷ fy+ cy \tag{2}
$$

$$
hi= zi \tag{3}
$$

然后可以通过对第k个单元中点云的hik值求平均来计算高度期望：

$$
µ(qi) k i= 1 n
n
∑
j=1
hikj, n ≥ 3 \tag{4}
$$

进一步计算相邻单元之间的高度梯度，以滤除低梯度特征：

$$
grad(qi) r i= µ(qi) r+1 i − µ(qi) r i \tag{5}
$$

$$
grad(qi) c i= µ(qi) c+1 i − µ(qi) c i \tag{6}
$$

2)直接匹配方法：

视觉SLAM[18]中的直接法基于光照不变性的假设来优化光度误差。类似地，高度不变性的假设依赖于激光雷达俯仰角的补偿，在车辆行驶过程中也可以成立。因此，采用直接法进行2.5D高程图的匹配。

将第i帧中的第k个单元的高度图 zik 视为测量值，用于计算高度差误差（HDE） eik：

$$
eik= zik − µ(m(Ti ∗pi−1)) k i \tag{7}
$$

其中 Ti ∗ pi−1 定义了从前一帧 i−1 到当前帧 i的变换， m表示从三维点云到2.5维高度图的投影步骤。

目标函数 Ji 被定义为一个最小二乘问题，用于求解相对位姿 Ti：

$$
Ji=∑
k ∈C e k i(Ti)
T
Ωe k i(Ti) \tag{8}
$$

其中 C是2.5D高度图中所有栅格的集合，Ω表示信息矩阵，即误差 e k i 的协方差矩阵的逆矩阵。

在直接法中，引入李代数 ξ i来推导雅可比矩阵 J k i ，该矩阵可根据链式法则分为三个部分：

$$
J k i = δe k i
δξ i
= − δµ i δqi δqi δpi δpi
δξ i
\tag{9}
$$

其中第一部分 δµ i
δ q i
是网格的偏导数，即网格梯度，δ q i
δ p i
是网格对三维空间点的偏导数，δ p i
δξ i
是三维空间点对李代数的偏导数。通过高斯‐牛顿法得到的最终解如下：

$$
(
C
∑
k=1 Jk i T Jk i)δξ∗ i= − C
∑
k=1 Jk i T eik \tag{10}
$$

B.基于2.5D段的回环检测

1)2.5维段：

回环检测与优化是SLAM系统的基础。然而，由于直接匹配方法需要良好的初始估计才能进行优化，因此无法将其用于2.5D高程图的该任务。受SegMatch方法[12],的启发，我们从2.5D高度图中提取2.5维段，并采用直方图来辅助回环闭合检测。

从之前构建的2.5维地图中，我们使用K‐均值方法获得2.5维段，如图2所示。

通过将相邻的网格单元递归地聚类为一个段，获得网格中所有具有相应区域和高度信息的段。

示意图1

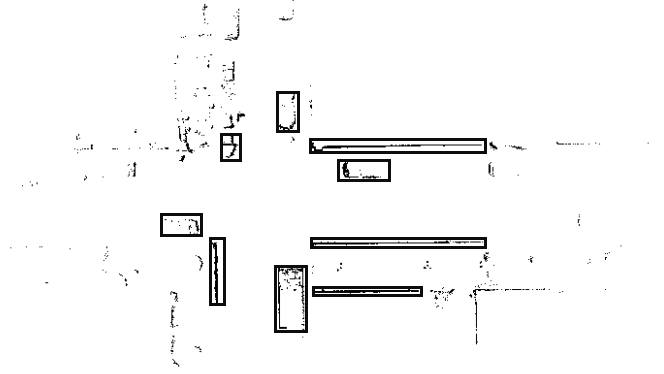
SegMatch中的段特征[12]通过基于3D体素的形状直方图、线性度、平面度和散射度来描述。在我们的方法中，为每个段定义了五种描述符，即主方向、高度梯度、曲率、全向方差和特征熵，用于后续的匹配过程。主方向和特征值不仅表示二维平面上的特征，还包含高度方向的信息，从而构成每个段的2.5维特定特征。

主成分描述了每个段 Si的方向特征，该段由聚类得到的相应投影点组成。对于每个点qi(ri, ci, hi)， ri和 ci分别表示在栅格中行和列的单元索引， hi表示位于该栅格中的高度值。

根据主成分分析（PCA）¯算法，我们计算期望 r¯, ¯c, h和相应的协方差矩阵 Σ：

$$
r¯= 1 n
n
∑
i=1
r i , ¯c= 1 n
n
∑
i=1
c i , ¯h= 1 n
n
∑
i=1
h i \tag{11}
$$

$$
σ(r, c)= 1 n
n
∑
i=1 (ri − r¯) T (ci − ¯c) \tag{12}
$$

$$
Σ= \begin{bmatrix}
σ(r, r) & σ(r, c) & σ(r, h) \
σ(c, r) & σ(c, c) & σ(c, h) \
σ(h, r) & σ(h, c) & σ(h, h)
\end{bmatrix} \tag{13}
$$

由于协方差矩阵 Σ 是对称正定的，它可以分解为正交矩阵 Q 和对角矩阵 Λ的乘积。

$$
Σ= QΛQ−1 \tag{14}
$$

然后，我们基于特征分解方法求解最大特征值 λ1, λ2, λ3及其对应的特征向量v~1(d1, l1, γ1)、v~2(d2, l2, γ2)、 v~3(d3, l3, γ3)，以得到主方向。

$$
Q=(v~1,v~2,v~3),Λ= diag(λ1, λ2, λ3) \tag{15}
$$

由公式和公式(6)计算出的高度差构成了高度描述符 hg(grad(h)ri, grad(h)ic)。 (5)

曲率 cr反映表面偏差，全向方差 ov表示散射程度，特征熵 ee特征由特征值和给定阈值[19]计算得出。

$$
cr=
λ3 λ1+ λ2+ λ3
÷ cre \tag{16}
$$

$$
ov=(λ1λ2λ3)^{1/3} ÷ ove \tag{17}
$$

$$
ee=(λ1log(λ1)+ λ2log(λ2)+ λ3log(λ3))÷ eee \tag{18}
$$

上述计算得到的描述符构成了最终的多维度特征向量 f，作为每个段的唯一标识符。基于该特征向量，可进行后续的回环闭合检测过程。

$$
f=(v1^T, v2^T, v3^T, hg^T, cr, ov, ee) \tag{19}
$$

2)回环闭合检测：

类似于SegMap[12],，当前2.5D高度图中每个段的所有特征通过计算对应特征向量之间的得分，与参考高度图中段的特征进行匹配：

$$
scoreij =
m
∑
k=1
(fi(k)− fj(k))^2 \tag{20}
$$

其中 scorei j 是用于识别回环检测的特征向量的欧氏距离， m是特征向量的维度。然后，通过将计算得到的score i j 与先验阈值 c进行比较，得到候选匹配集 C。

$$
C={(fi , fj) |scorei j ≤ c} \tag{21}
$$

此外，我们还设置了最小时间阈值 t来过滤候选匹配，以避免在相邻帧之间出现错误的回环闭合检测。

$$
C′ ={(fi , f j) |fi .time− f j .time ≥ t} \tag{22}
$$

一旦检测到回环检测，将在匹配帧之间向位姿图添加一个新的约束。

3)位姿图优化：

我们使用g2o[20]框架来求解优化问题。在第一个目标函数 Ji中，当获取到两帧连续的激光雷达扫描 pi−1和 pi时，将HDE的边约束添加到图中以优化节点 xi。

$$
Ji=∑
k∈C
eik(xi,pi−1,pi)^T Ω eik(xi,pi−1,pi) \tag{23}
$$

对于回环图，假设在 xi和xj处发生闭环，对应的激光雷达扫描为 pi和 pj。通过最小化误差函数 Jil来更新位姿 xi：

$$
Jir= eri(xi,pi,pj)^T R eri(xi,pi,pj) \tag{24}
$$

在图中，位姿节点 x∗ i通过给定两帧点云在高度差误差和回环检测约束下同时求解。

$$
x∗ i= arg minxi( Jir+ Ji) \tag{25}
$$

IV.实验

A.数据集

我们在KITTI[21]里程计数据集上评估了我们的方法。本文展示了序列00、05、08、03、14和16的结果，因为这些序列在数据集中表现出足够的变化。我们将DLO和LOAM算法生成的结果与我们的结果进行了比较。

在所有实验中，我们仅使用了Velodyne数据，未借助惯性测量单元。操作系统为Ubuntu16.04，计算平台配备i7‐6800K处理器和16GB内存。

我们算法中的参数和阈值设置如下：2.5D高度图的网格分辨率 fx=fy = 0.2，车辆中心位置 cx= c y = 400，曲率阈值 cre= 1，全向方差 ove=0.3，熵 eee= 0.9，评分先验阈值 c= 0.35，候选匹配最短时间 t= 0.2s。

LOAM的参数如下：N‐Scan=64，cornerPointsSharp number= 8，cornerPointsLessSharpnumber= 35，surfPointsFlatnumber= 10，downSizeFilter=0.5。

B.结果

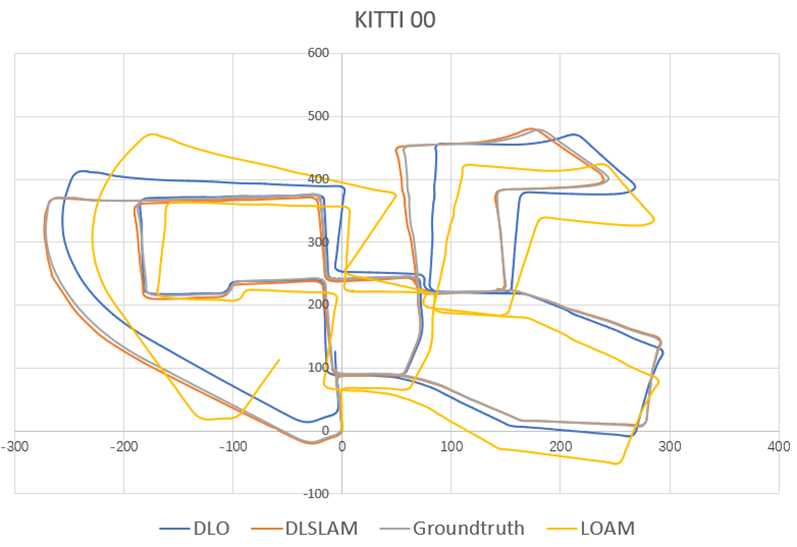
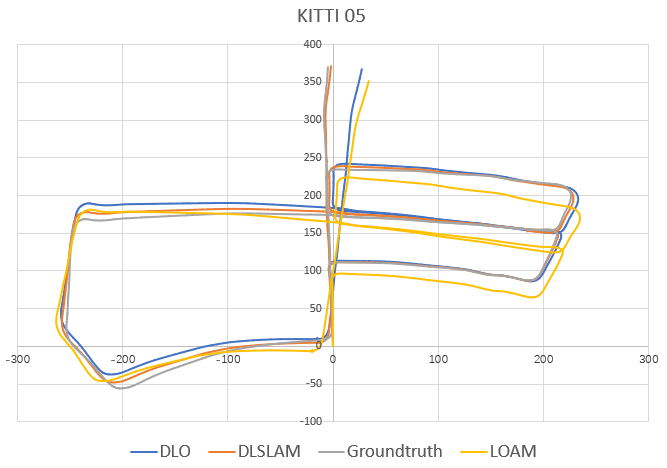
序列00、05、08和03生成的轨迹如图4所示。这些序列提供了用于评估的真实值。可以清楚地看到，DLO和LOAM的轨迹在开始时与真实值吻合，但随着车辆行驶距离变长，由于误差累积，不可避免地产生了较大的漂移。DL‐SLAM在序列00上耗时150秒检测到5个回环，并成功匹配了总共748帧。序列14和16的结果与LOAM和DLO的比较如图5所示，呈现了类似的结果。

尽管图中显示的是二维顶视图，但在许多自动驾驶路径规划的情况下，无需考虑三维位姿信息。

示意图2

示意图3

C.评估

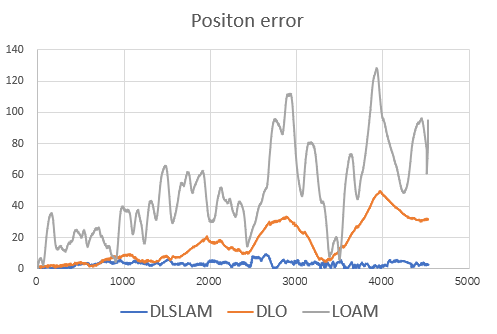
我们根据KITTI标准开发工具包采用了相对平移误差(RTE)和相对旋转误差(RRE)作为误差度量，该工具包提供了6自由度误差信息。

RTE由结果位姿与真实值位姿之间的平均位置误差定义。KITTI序列00上的相应误差如图3所示。

$$
RT Ei= \sqrt{(x′_i − x_i)^2+(y′_i − y_i)^2+(z′_i − z_i)^2} \tag{26}
$$

$$
RT E= \sum_{i=1}^{k} RT E_i ÷ k \tag{27}
$$

示意图4

RRE由计算结果 $ R’_i $与真实值 $ R_i $之间的平均旋转误差 $ Rrmi $定义。

$$
R_i = R_{yi} \cdot R_{pi} \cdot R_{ri} \tag{28}
$$

$$
Rrmi = inv(R_i) \cdot R’_i \tag{29}
$$

$$
Rerror_i = \frac{1}{2}(trace(Rrmi) - 1) \tag{30}
$$

$$
RRE_i = \arccos(\max(\min(Rerror_i, 1.0), -1.0)) \tag{31}
$$

$$
RRE = \sum_{i=1}^{k} RRE_i ÷ k \tag{32}
$$

从表I可以看出，DL‐SLAM的平均位置误差不超过3.5米，优于DLO和LOAM。DL‐SLAM将旋转误差降低至0.15度以内，并始终通过回环检测校正位置，避免了较大的漂移，满足精度要求。

表I DLO、LOAM和DL‐SLAM的RTE与 RRE

	DLO	LOAM	DL‐SLAM
RTE 00 03 05 08	16.4547 3.2015 10.0289 14.7745	40.3504 12.9083 20.7452 23.4713	3.1498 2.2438 3.2181 3.4331
RRE 00 03 05 08	0.4737 0.1475 0.4757 0.4816	1.0141 0.3518 0.6647 0.7493	0.1488 0.1355 0.1470 0.1503

表II DL‐SLAM、DLO和LOAM的运行时间对比（总秒数和每帧平均秒数）

	DLO	LOAM	DLSLAM
00	403.474s / 0.089s	744.739s / 0.164s	603.742s / 0.133s
03	50.778s / 0.063s	116.626s / 0.146s	56.671s / 0.071s
05	196.357s / 0.071s	438.002s / 0.159s	259.534秒 / 0.094秒
08	268.275秒 / 0.066秒	696.141秒 / 0.171秒	354.177秒 / 0.087秒