8.5 中心
- Chebyshev中心
- 最大体积椭球中心
- 不等式组的解析中心
Chebyshev中心
多面体的Chebyshev中心
设C是有线性不等式组 定义,如果
定义,如果 ,则
,则

于是Chebyshev中心可以通过求解线性规划:


最大体积椭球中心
定义C中具有最大体积椭球的中心为C的最大体积椭球中心,记为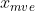 ,如下图。
,如下图。

不等式组的解析中心
一组凸不等式和线性方程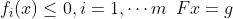 的解析中心
的解析中心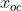 定义为凸问题
定义为凸问题
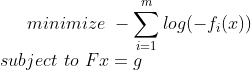
的最优解。这里的优化变量是 ,并有隐含约束
,并有隐含约束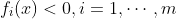 。问题中的目标被称为与不等式相关的对数障碍。
。问题中的目标被称为与不等式相关的对数障碍。
解析中心不是有不等式和等式所描述的集合的函数;两组不等式和等式可能定义相同的集合,但有不同的解析中心。
线性不等式组的解析中心
线性不等式组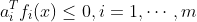 的解析中心是下面无约束极小化问题的解:
的解析中心是下面无约束极小化问题的解:
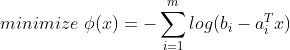
其隐含约束为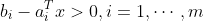
可以对线性不等式组的解析中心给予几何解释。因为解析中心对约束函数的正伸缩变换独立,可以不失一般性地假设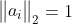 ,在这种情况下,
,在这种情况下,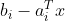 的松弛是到超平面
的松弛是到超平面
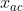 是
是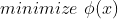 的最优解,下图虚线是多面体C的对数障碍函数的五条等值曲线,对数障碍函数的最小值点是
的最优解,下图虚线是多面体C的对数障碍函数的五条等值曲线,对数障碍函数的最小值点是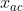 。
。

内部阴影所示的椭球为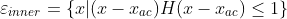 其中H为对数障碍函数
其中H为对数障碍函数 在
在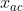 处的海瑟矩阵。
处的海瑟矩阵。
定义
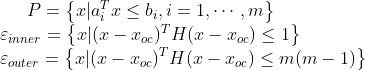
则有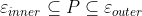 ,即
,即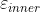 总是在P中,而
总是在P中,而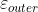 总是覆盖P。与最大体积内接椭球相比,这是一个较弱的结果。
总是覆盖P。与最大体积内接椭球相比,这是一个较弱的结果。
来源:https://blog.youkuaiyun.com/wangchy29/article/details/87875533








 博客主要介绍了几种中心的概念。包括多面体的Chebyshev中心,可通过求解线性规划得出;最大体积椭球中心是C中最大体积椭球的中心;还阐述了不等式组的解析中心,包括一般情况及线性不等式组的解析中心,并给出了相关定义和几何解释。
博客主要介绍了几种中心的概念。包括多面体的Chebyshev中心,可通过求解线性规划得出;最大体积椭球中心是C中最大体积椭球的中心;还阐述了不等式组的解析中心,包括一般情况及线性不等式组的解析中心,并给出了相关定义和几何解释。
















 282
282

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








