7.5 实验设计
- 松弛实验设计问题
- 标量化
考虑通过测量或实验: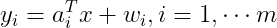 估计向量
估计向量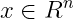 的问题,其中
的问题,其中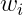 是测量噪声。假设
是测量噪声。假设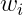 是独立同分布的高斯噪声,均值为0,方差为1。
是独立同分布的高斯噪声,均值为0,方差为1。
于是x的最大似然估计,也是最小方差估计:
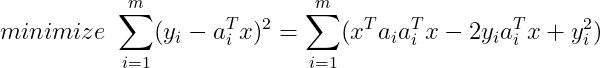
目标函数对x求偏导,得到:
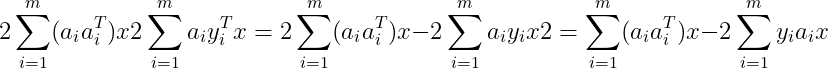
令其为0,解得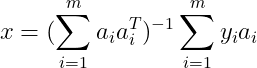 ,故极大似然估计的解为:
,故极大似然估计的解为: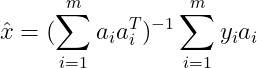 相应的估计误差:
相应的估计误差: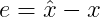 均值为0,协方差矩阵:
均值为0,协方差矩阵:
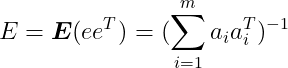
矩阵E刻画了估计经度或是实验的信息度。
例如x的 -置信水平椭圆为:
-置信水平椭圆为: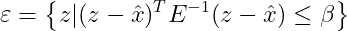
其中 是常熟,由n和
是常熟,由n和 决定。
决定。
假设刻画测量值的向量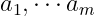 可以从p中可能的检验向量
可以从p中可能的检验向量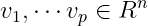 进行选择,即每个
进行选择,即每个 是
是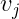 中的一个。
中的一个。
实验设计:从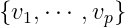 选择
选择 以使得E极小。
以使得E极小。
令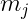 表示
表示 选择值
选择值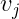 得试验次数,则
得试验次数,则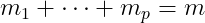 ,于是协方差矩阵可以描述为:
,于是协方差矩阵可以描述为:
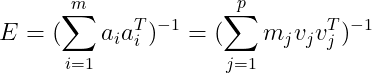
于是实验设计问题可以表述为:
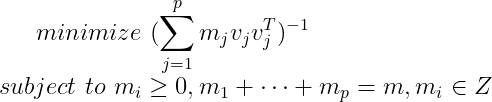
Z表示整数。
松弛实验设计问题
因为实验设计问题对 的征整数的约束们额头很难求解,于是提出松弛实验设计问题。
的征整数的约束们额头很难求解,于是提出松弛实验设计问题。
在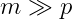 的时候,令
的时候,令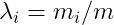 表示
表示 的试验次数与总的试验次数的比值,忽略对
的试验次数与总的试验次数的比值,忽略对 的整数约束,于是得到:
的整数约束,于是得到:
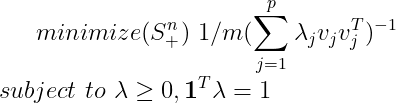
其中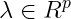 。
。
标量化
D-最优设计
极小化误差协方差矩阵E的绝对值,即设计实验,计息哦啊好对应的执行椭球的体积,忽略E中的常数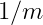 ,对目标函数求导,得到:
,对目标函数求导,得到:
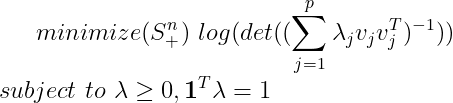
此问题是一个凸优化问题。
E-最优设计
极小化误差协方差矩阵的范数,即E的最大特征值,即:
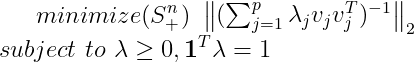
也可以写成:
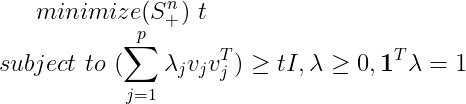
其中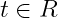
A-最优设计
极小化误差协方差矩阵的迹,即:
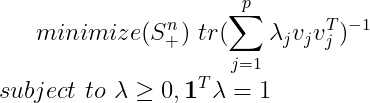
最优设计实验及对偶
D-最优实验设计的对偶问题:
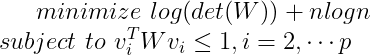
优化变量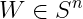 ,定义域为
,定义域为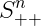 。
。
解释:最优解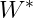 决定了一个以原点为中心,包含点
决定了一个以原点为中心,包含点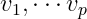 的最小体积椭球
的最小体积椭球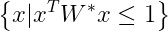
根据互补松弛性有,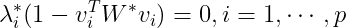 。
。
来源:https://blog.youkuaiyun.com/wangchy29/article/details/87471247
























 1534
1534

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








