一、为什么使用序列模型
能处理非固定大小输入的问题,例如语音识别,DNA序列分析,机器翻译这种是一串序列的问题。
二、 数学符号表示
以自然语言处理为例:
x: Harry Potter and Hermione Granger invented a new spell.
以这句话为输入x,希望得到一个相同长度的y,判断每个单词是否表示人名。
首先需要构建一个按字母排序的单词词典,当然该词典中包含单词的个数因网络和计算资源的不同而不同,一般有4000个等,在这里我们为了表示方便,假设单词数量为1000。然后将每个单词对应在字典中的位置,映射成一个长度为1000的一维向量(onehot)。具体表示方法如下所示:
| 符号 | 说明 |
|---|---|
| X<1>=[0,0,0,1,0,0,...,0,0]X^{<1>}=[0, 0, 0, 1, 0, 0, ..., 0, 0]X<1>=[0,0,0,1,0,0,...,0,0] | X<i>X^{<i>}X<i>表示该句话的第iii个单词,在此处表示Harry在词典中序号为4。 |
| Y<i>Y^{<i>}Y<i> | 表示第iii个单词的输出。 |
| Tx=9T_x = 9Tx=9 | 这个序列的长度为9 |
| Ty=9T_y = 9Ty=9 | 这个序列的输出长度为9 |
| X(i)<t>X^{(i)<t>}X(i)<t> | 样本中第iii个序列的第ttt个单词 |
| Tx(i)T_x^{(i)}Tx(i) | 样本中第iii个输入序列的长度 |
注意:如果样本中出现了词典中不包含的单词,需要定义一个Unknown向量,以及每句话的结尾EOS向量。
三、循环神经网络模型
1 为什么不能用标准的神经网络
- 在序列输入问题中,大部分的输入不能输出都不能统一
- 在同一个单词在文本的不同位置不能分享特征
2 循环神经网络
2.1 前向传播
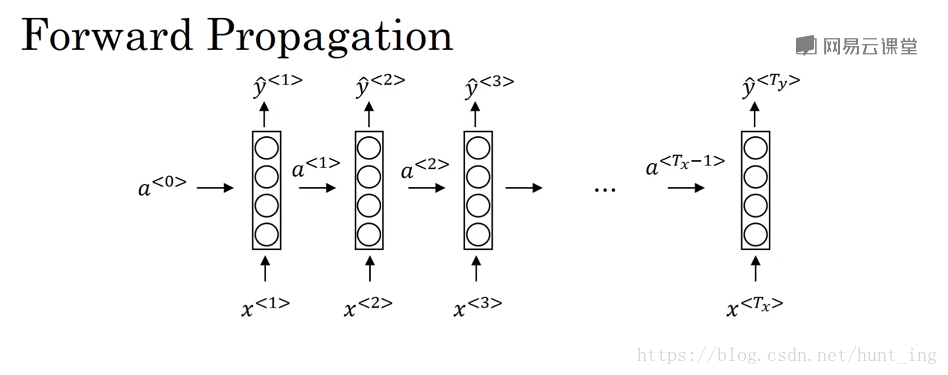
a<t>=g1(Waaa<t−1>+Waxx<t>+ba)a^{<t>}=g_1(W_{aa}a^{<t-1>}+W_{ax}x^{<t>}+b_a)a<t>=g1(Waaa<t−1>+Waxx<t>+ba)
y^=g2(Wyaa<t>+by)\hat y=g_2(W_{ya}a^{<t>}+b_y)y^=g2(Wyaa<t>+by)
公式可以简化为
a<t>=g1(Wa[a<t−1>,x<t>]+ba)a^{<t>}=g_1(W_{a}[a^{<t-1>},x^{<t>}]+b_a)a<t>=g1(Wa[a<t−1>,x<t>]+ba)
y^=g2(Wya<t>+by)\hat y=g_2(W_{y}a^{<t>}+b_y)y^=g2(Wya<t>+by)
2.2 方向传播
对于一个判断是否为人名的二分类问题,可以定义损失函数:
KaTeX parse error: Expected 'EOF', got '\cal' at position 2: \̲c̲a̲l̲ ̲L^{<t>}(\hat y^…
通过梯度下降算法不断更新参数
时间反向传播(backpropagation through time)
2.3 不同类型的循环神经网络
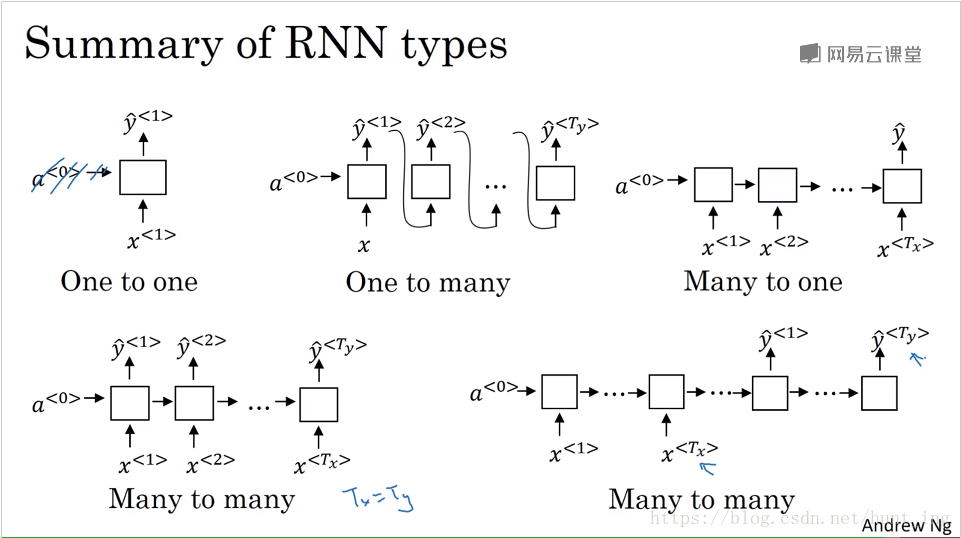
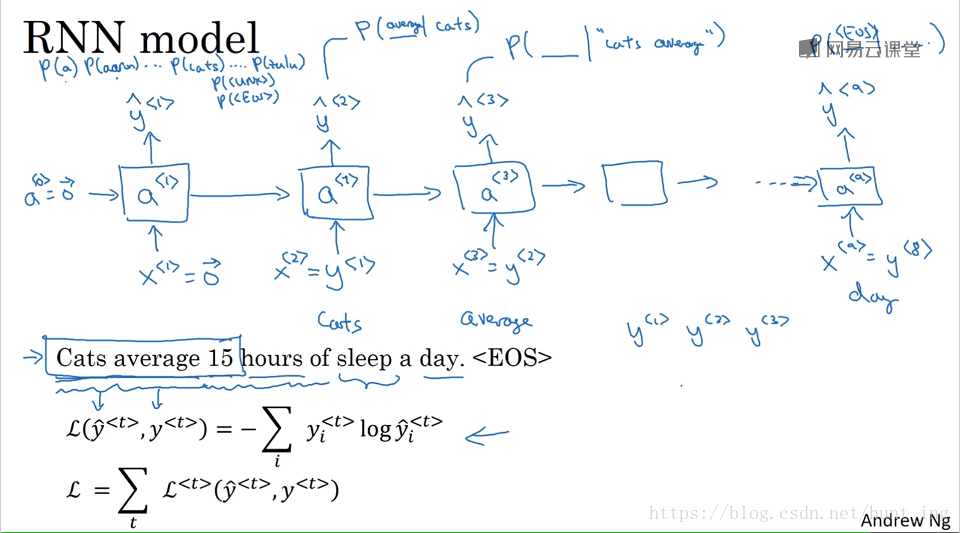
3 语言模型和序列生成
3.1 生成过程
一句话概括就是:单词出现的概率。
需要训练集:一个大的语料库(corpus of English text 数量众多的句子)
3.2 生成采样
通过每个单元生成的softmax概率,然后以每个单词的概率做随机,到第二个单元时以第一个单元的结果为输入,然后再生成softmax概率,如此循环直到生成EOS标志或者限定时间数。
3.3 字符模型
相比较词汇模型而言,字符模型是以字母,标点符号,数字为字典元素。相比较词汇模型而言,会得到更多的输入,网络相对更加深,训练起来计算成本也比较昂贵。
4 梯度问题
梯度爆炸:梯度修剪
梯度消失:GRU,LSTM
4.1 GRU(Gated Recurrent Unit 门控循环单元)
学习非常深的连接
相关论文:On the properties of neural machine translation:Encoder-decoder approaches 2014
Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling 2014

c^<t>=tanh(Wc[c<t−1>,x<t>]+bc)\hat c^{<t>}=\tanh (W_c[c^{<t-1>},x^{<t>}]+b_c)c^<t>=tanh(Wc[c<t−1>,x<t>]+bc)
Γu=σ(Wu[c<t−1>,x<t>]+bu)\Gamma_u= \sigma (W_u[c^{<t-1>},x^{<t>}]+b_u)Γu=σ(Wu[c<t−1>,x<t>]+bu)
c<t>=Γu∗c^<t>+(1−Γu)∗c<t−1>c^{<t>}=\Gamma_u * \hat c^{<t>}+(1-\Gamma_u)*c^{<t-1>}c<t>=Γu∗c^<t>+(1−Γu)∗c<t−1>
a<t>=c<t>a^{<t>}=c^{<t>}a<t>=c<t>
Full GRU
c^<t>=tanh(Wc[Γr∗c<t−1>,x<t>]+bc)\hat c^{<t>}=\tanh (W_c[\Gamma_r*c^{<t-1>},x^{<t>}]+b_c)c^<t>=tanh(Wc[Γr∗c<t−1>,x<t>]+bc)
Γu=σ(Wu[c<t−1>,x<t>]+bu)\Gamma_u= \sigma (W_u[c^{<t-1>},x^{<t>}]+b_u)Γu=σ(Wu[c<t−1>,x<t>]+bu)
Γr=σ(Wr[c<t−1>,x<t>]+br)\Gamma_r=\sigma(W_r[c^{<t-1>},x^{<t>}]+b_r)Γr=σ(Wr[c<t−1>,x<t>]+br)
c<t>=Γu∗c^<t>+(1−Γu)∗c<t−1>c^{<t>}=\Gamma_u * \hat c^{<t>}+(1-\Gamma_u)*c^{<t-1>}c<t>=Γu∗c^<t>+(1−Γu)∗c<t−1>
a<t>=c<t>a^{<t>}=c^{<t>}a<t>=c<t>
4.1 LSTM(Long Short Term Memory Unit 长短时记忆单元)
学习非常深的连接
相关论文:Long short-term memory 1997
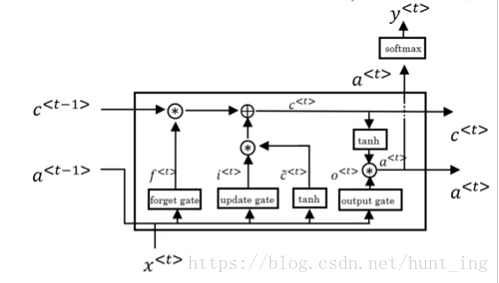
c^<t>=tanh(Wc[a<t−1>,x<t>]+bc)\hat c^{<t>}=\tanh (W_c[a^{<t-1>},x^{<t>}]+b_c)c^<t>=tanh(Wc[a<t−1>,x<t>]+bc)
Γu=σ(Wu[a<t−1>,x<t>]+bu)\Gamma_u= \sigma (W_u[a^{<t-1>},x^{<t>}]+b_u)Γu=σ(Wu[a<t−1>,x<t>]+bu)
Γf=σ(Wf[a<t−1>,x<t>]+bf)\Gamma_f= \sigma (W_f[a^{<t-1>},x^{<t>}]+b_f)Γf=σ(Wf[a<t−1>,x<t>]+bf)
Γo=σ(Wo[a<t−1>,x<t>]+bo)\Gamma_o= \sigma (W_o[a^{<t-1>},x^{<t>}]+b_o)Γo=σ(Wo[a<t−1>,x<t>]+bo)
c<t>=Γu∗c^<t>+Γf∗c<t−1>c^{<t>}=\Gamma_u * \hat c^{<t>}+\Gamma_f*c^{<t-1>}c<t>=Γu∗c^<t>+Γf∗c<t−1>
a<t>=Γo∗tanhc<t>a^{<t>}=\Gamma_o*\tanh c^{<t>}a<t>=Γo∗tanhc<t>
5 双向循环神经网络(Bidirectional RNN) (BRNN)
因为语言有上下文的语境关系,所以采用双向循环,是的特征信息能够保全得更加完整。
深层循环神经网络
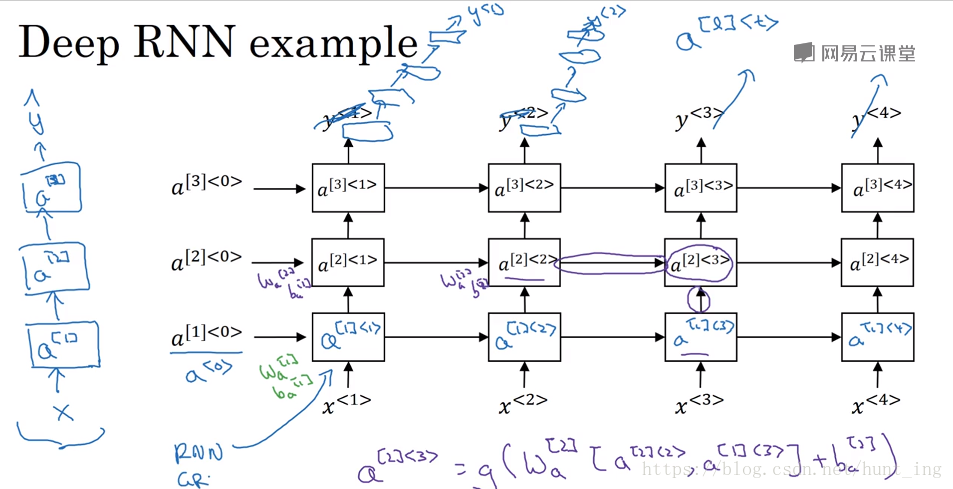
因为循环神经网络本身在时间流上就很深,因此,在空间叠加上,不能过深。
测试题
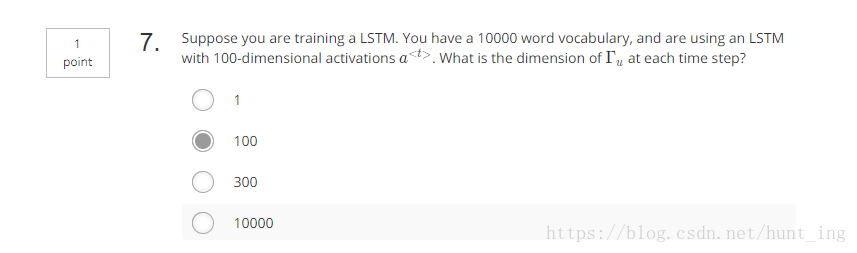





 本文介绍了序列模型解决非固定大小输入问题的优势,并详细探讨了循环神经网络(RNN)的工作原理,包括其数学表示、前向传播过程及解决梯度问题的方法如GRU和LSTM。同时,还讨论了不同类型的RNN及其在自然语言处理任务中的应用。
本文介绍了序列模型解决非固定大小输入问题的优势,并详细探讨了循环神经网络(RNN)的工作原理,包括其数学表示、前向传播过程及解决梯度问题的方法如GRU和LSTM。同时,还讨论了不同类型的RNN及其在自然语言处理任务中的应用。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








