洛谷P1216 数字三角形题解

原创于 2025-04-13 11:16:50 发布 · 1.6k 阅读

35 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #记忆化搜索 #动态规划

题目传送门

题目描述

观察下面的数字金字塔。

写一个程序来查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。

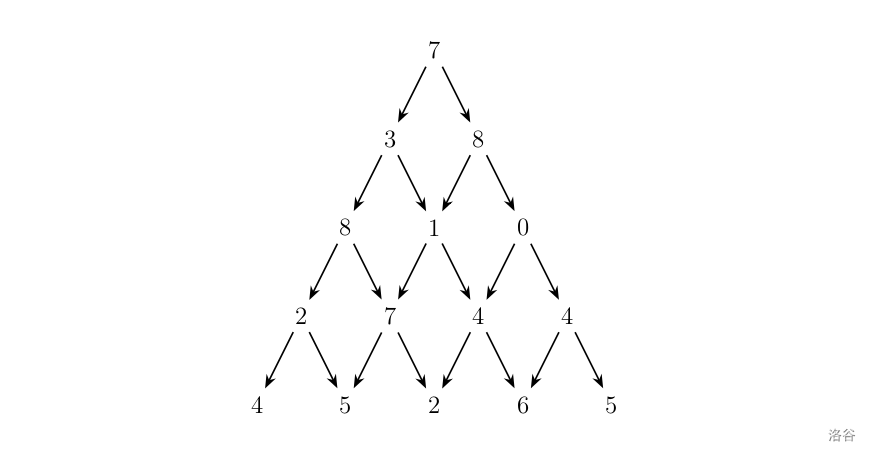
在上面的样例中，从 7→3→8→7→5 的路径产生了最大权值。

输入格式

第一个行一个正整数 r ,表示行的数目。

后面每行为这个数字金字塔特定行包含的整数。

输出格式

单独的一行,包含那个可能得到的最大的和。

输入输出样例

输入 #1复制

输出 #1复制

说明/提示

【数据范围】
对于 100% 的数据，1≤r≤1000，所有输入在 [0,100] 范围内。

题目翻译来自NOCOW。

USACO Training Section 1.5

IOI1994 Day1T1

分析

首先，贪心明显是不行的，在样例中会得到7-8-1-7-5路径和为28，但有一条最优路径为7-3-8-7-5和为30，所以贪心是错误的策略。

方法一：搜索

对此采取深度优先搜索，定义dfs(int x,int y,int sum)函数，其中x,y表示已经从(1,1) 走到(x,y)，sum表示当前和，当x=n时，如果sum>ans，则更新答案。

#include<bits/stdc++.h>
using namespace std;
#define MAXN 1005
int a[MAXN][MAXN],n,ans;
void dfs(int x,int y,int sum){
    if(x==n){ //到达递归边界
        if(sum>ans) ans=sum; //如果当前解更优，更新答案
        return; //回溯
    }
    dfs(x+1,y,sum+a[x+1][y]); //递归到左下元素
    dfs(x+1,y+1,sum+a[x+1][y+1]); //递归到右下元素
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++)
            scanf("%d",&a[i][j]);
    dfs(1,1,a[1][1]); //搜索
    printf("%d",ans);
    return 0;
}

很明显搜索的时间复杂度为O(2^n-1)，喜提TLE。

方法二：记忆化搜索

直接搜索之所以超时，是因为有大量的重复计算，用f[x][y]表示从(x,y)走到终点的路径和。

#include<bits/stdc++.h>
using namespace std;
int a[1010][1010],f[1010][1010],n;
int dfs(int x,int y){
    if(f[x][y]!=-1) return f[x][y];// 如果计算过就直接返回
    if(x==n) f[x][y]==a[x][y]; // 如果到达递归边界就返回数字
    else f[x][y]=max(dfs(x+1,y),dfs(x+1,y+1))+a[x][y];
    return f[x][y];
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            scanf("%d",&a[i][j]);
            f[i][j]=-1;
        }  
    } 
    dfs(1,1);
    printf("%d\n",f[1][1]);
    return 0;
}

由于对每个f[x][y]只计算过一次，所以时间复杂度为O(n^2)，可以通过此题。

方法三：动态规划（逆推）

看上面的代码：f[x][y]=max(dfs(x+1,y),dfs(x+1,y+1))+a[x][y];

其实这已经是状态转移方程方程的雏形了，试着把dfs换成f数组，就是本题的状态转移方程：

f[x][y]=max(f[x+1][y],f[x][y+1])+a[x][y]

很容易得到代码

#include<bits/stdc++.h>
using namespace std;
int a[1010][1010],f[1010][1010],n;
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            scanf("%d",&a[i][j]);
        }  
    }
    for(int i=n-1;i>=1;i--){
        for(int j=1;j<=i;j++){
            f[i][j]=max(f[i+1][j],f[i+1][j+1])+a[i][j];
        }  
    }  
    printf("%d\n",f[1][1]);
    return 0;
}

~~完结撒花~~

有错误请指出