一、图:关系网络的数学表示
1.1 图的基本概念与术语
图是一种非线性的数据结构,由顶点(Vertex) 和边(Edge) 组成,用于表示多对多的关系。图结构能够很好地描述现实世界中的各种网络关系。
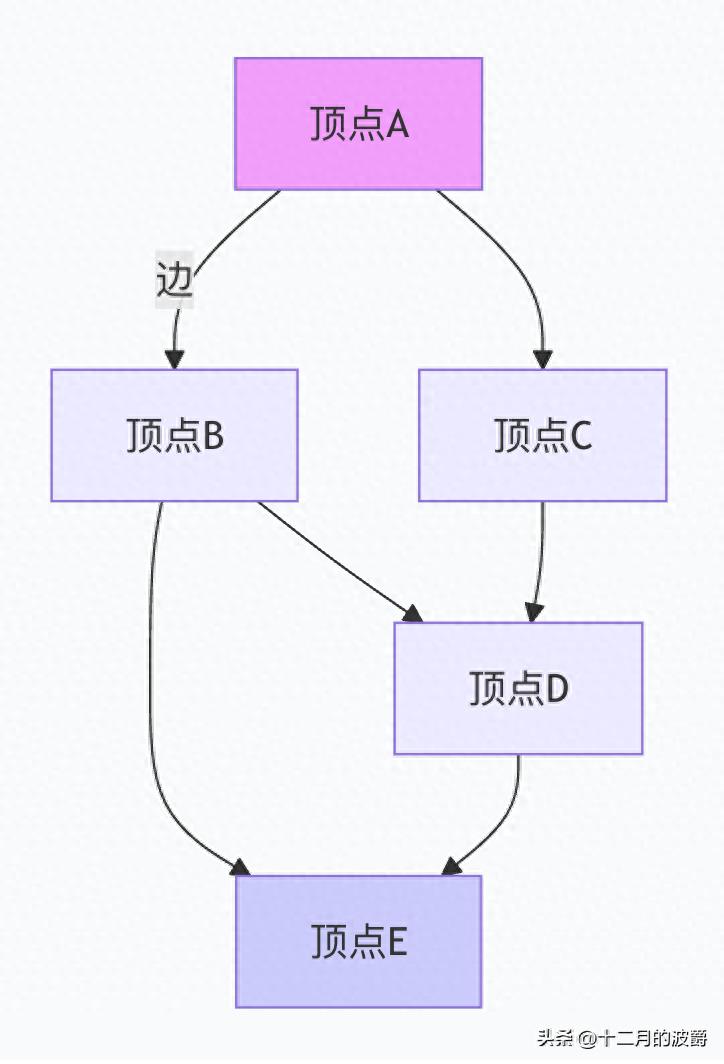
核心术语:
- 顶点(Vertex/Node):图的基本元素,表示实体
- 边(Edge):顶点之间的连接,表示关系
- 有向图/无向图:边是否有方向性
- 权重(Weight):边的权值,表示距离、成本等
- 度(Degree):与顶点相连的边数
- 路径(Path):顶点序列,其中每个顶点与下一个顶点相连
- 连通图(Connected Graph):任意两个顶点间都有路径相连
1.2 图的表示方式
邻接矩阵表示法:
public class GraphMatrix {
private int[][] adjacencyMatrix;
private int vertexCount;
public GraphMatrix(int vertexCount) {
this.vertexCount = vertexCount;
this.adjacencyMatrix = new int[vertexCount][vertexCount];
}
public void addEdge(int source, int destination, int weight) {
adjacencyMatrix[source][destination] = weight;
// 对于无向图,还需要添加反向边
// adjacencyMatrix[destination][source] = weight;
}
public boolean isAdjacent(int source, int destination) {
return adjacencyMatrix[source][destination] != 0;
}
public List<Integer> getNeighbors(int vertex) {
List<Integer> neighbors = new ArrayList<>();
for (int i = 0; i < vertexCount; i++) {
if (adjacencyMatrix[vertex][i] != 0) {
neighbors.add(i);
}
}
return neighbors;
}
}
邻接表表示法(更节省空间):
public class GraphList {
private Map<Integer, List<Edge>> adjacencyList;
private int vertexCount;
static class Edge {
int destination;
int weight;
Edge(int destination, int weight) {
this.destination = destination;
this.weight = weight;
}
}
public GraphList(int vertexCount) {
this.vertexCount = vertexCount;
this.adjacencyList = new HashMap<>();
for (int i = 0; i < vertexCount; i++) {
adjacencyList.put(i, new ArrayList<>());
}
}
public void addEdge(int source, int destination, int weight) {
adjacencyList.get(source).add(new Edge(destination, weight));
// 对于无向图,还需要添加反向边
// adjacencyList.get(destination).add(new Edge(source, weight));
}
public List<Edge> getNeighbors(int vertex) {
return adjacencyList.get(vertex);
}
}
二、图的遍历算法
2.1 广度优先搜索(BFS)
BFS按照层次的顺序遍历图,先访问离起点最近的顶点。
public class BFS {
public static void bfsTraversal(GraphList graph, int startVertex) {
boolean[] visited = new boolean[graph.vertexCount];
Queue<Integer> queue = new LinkedList<>();
visited[startVertex] = true;
queue.offer(startVertex);
while (!queue.isEmpty()) {
int currentVertex = queue.poll();
System.out.print(currentVertex + " ");
for (GraphList.Edge edge : graph.getNeighbors(currentVertex)) {
if (!visited[edge.destination]) {
visited[edge.destination] = true;
queue.offer(edge.destination);
}
}
}
}
// 查找最短路径(未加权图)
public static int[] shortestPathUnweighted(GraphList graph, int startVertex) {
int[] distances = new int[graph.vertexCount];
Arrays.fill(distances, -1);
Queue<Integer> queue = new LinkedList<>();
distances[startVertex] = 0;
queue.offer(startVertex);
while (!queue.isEmpty()) {
int currentVertex = queue.poll();
for (GraphList.Edge edge : graph.getNeighbors(currentVertex)) {
if (distances[edge.destination] == -1) {
distances[edge.destination] = distances[currentVertex] + 1;
queue.offer(edge.destination);
}
}
}
return distances;
}
}
2.2 深度优先搜索(DFS)
DFS沿着路径深入遍历,直到无法继续前进再回溯。
递归实现:
public class DFSRecursive {
public static void dfsTraversal(GraphList graph, int startVertex) {
boolean[] visited = new boolean[graph.vertexCount];
dfsUtil(graph, startVertex, visited);
}
private static void dfsUtil(GraphList graph, int vertex, boolean[] visited) {
visited[vertex] = true;
System.out.print(vertex + " ");
for (GraphList.Edge edge : graph.getNeighbors(vertex)) {
if (!visited[edge.destination]) {
dfsUtil(graph, edge.destination, visited);
}
}
}
// 检测图中是否有环
public static boolean hasCycle(GraphList graph) {
boolean[] visited = new boolean[graph.vertexCount];
boolean[] recStack = new boolean[graph.vertexCount];
for (int i = 0; i < graph.vertexCount; i++) {
if (hasCycleUtil(graph, i, visited, recStack)) {
return true;
}
}
return false;
}
private static boolean hasCycleUtil(GraphList graph, int vertex,
boolean[] visited, boolean[] recStack) {
if (recStack[vertex]) return true;
if (visited[vertex]) return false;
visited[vertex] = true;
recStack[vertex] = true;
for (GraphList.Edge edge : graph.getNeighbors(vertex)) {
if (hasCycleUtil(graph, edge.destination, visited, recStack)) {
return true;
}
}
recStack[vertex] = false;
return false;
}
}
迭代实现:
public class DFSIterative {
public static void dfsTraversal(GraphList graph, int startVertex) {
boolean[] visited = new boolean[graph.vertexCount];
Stack<Integer> stack = new Stack<>();
stack.push(startVertex);
while (!stack.isEmpty()) {
int currentVertex = stack.pop();
if (!visited[currentVertex]) {
visited[currentVertex] = true;
System.out.print(currentVertex + " ");
// 将邻接顶点逆序压栈,以保持与递归相同的遍历顺序
List<GraphList.Edge> neighbors = graph.getNeighbors(currentVertex);
for (int i = neighbors.size() - 1; i >= 0; i--) {
GraphList.Edge edge = neighbors.get(i);
if (!visited[edge.destination]) {
stack.push(edge.destination);
}
}
}
}
}
// 拓扑排序(仅适用于有向无环图)
public static List<Integer> topologicalSort(GraphList graph) {
boolean[] visited = new boolean[graph.vertexCount];
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < graph.vertexCount; i++) {
if (!visited[i]) {
topologicalSortUtil(graph, i, visited, stack);
}
}
List<Integer> result = new ArrayList<>();
while (!stack.isEmpty()) {
result.add(stack.pop());
}
return result;
}
private static void topologicalSortUtil(GraphList graph, int vertex,
boolean[] visited, Stack<Integer> stack) {
visited[vertex] = true;
for (GraphList.Edge edge : graph.getNeighbors(vertex)) {
if (!visited[edge.destination]) {
topologicalSortUtil(graph, edge.destination, visited, stack);
}
}
stack.push(vertex);
}
}
三、最短路径算法
3.1 Dijkstra算法
Dijkstra算法用于求解单源最短路径问题,适用于非负权重的图。
public class Dijkstra {
public static int[] dijkstra(GraphList graph, int source) {
int[] distances = new int[graph.vertexCount];
boolean[] visited = new boolean[graph.vertexCount];
Arrays.fill(distances, Integer.MAX_VALUE);
// 使用优先队列优化性能
PriorityQueue<Node> pq = new PriorityQueue<>(Comparator.comparingInt(n -> n.distance));
distances[source] = 0;
pq.offer(new Node(source, 0));
while (!pq.isEmpty()) {
Node currentNode = pq.poll();
int currentVertex = currentNode.vertex;
if (visited[currentVertex]) continue;
visited[currentVertex] = true;
for (GraphList.Edge edge : graph.getNeighbors(currentVertex)) {
int neighbor = edge.destination;
int newDistance = distances[currentVertex] + edge.weight;
if (newDistance < distances[neighbor]) {
distances[neighbor] = newDistance;
pq.offer(new Node(neighbor, newDistance));
}
}
}
return distances;
}
static class Node {
int vertex;
int distance;
Node(int vertex, int distance) {
this.vertex = vertex;
this.distance = distance;
}
}
// 重建最短路径
public static List<Integer> reconstructPath(int[] previous, int source, int target) {
List<Integer> path = new ArrayList<>();
for (int at = target; at != -1; at = previous[at]) {
path.add(at);
}
Collections.reverse(path);
if (path.get(0) == source) {
return path;
} else {
return Collections.emptyList(); // 路径不存在
}
}
}
3.2 Floyd-Warshall算法
适用于所有顶点对的最短路径问题,可以处理负权重(但不能有负权环)。
public class FloydWarshall {
public static int[][] floydWarshall(int[][] graph) {
int n = graph.length;
int[][] dist = new int[n][n];
// 初始化距离矩阵
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i == j) {
dist[i][j] = 0;
} else if (graph[i][j] != 0) {
dist[i][j] = graph[i][j];
} else {
dist[i][j] = Integer.MAX_VALUE / 2; // 防止溢出
}
}
}
// 动态规划核心
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (dist[i][k] + dist[k][j] < dist[i][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
// 检查负权环
for (int i = 0; i < n; i++) {
if (dist[i][i] < 0) {
throw new IllegalArgumentException("图中存在负权环");
}
}
return dist;
}
}
四、最小生成树算法
4.1 Prim算法
public class Prim {
public static int primMST(GraphList graph) {
int n = graph.vertexCount;
int[] key = new int[n];
boolean[] inMST = new boolean[n];
int[] parent = new int[n];
Arrays.fill(key, Integer.MAX_VALUE);
Arrays.fill(parent, -1);
key[0] = 0; // 从顶点0开始
PriorityQueue<Node> pq = new PriorityQueue<>(Comparator.comparingInt(n -> n.distance));
pq.offer(new Node(0, 0));
int mstWeight = 0;
while (!pq.isEmpty()) {
Node node = pq.poll();
int u = node.vertex;
if (inMST[u]) continue;
inMST[u] = true;
mstWeight += node.distance;
for (GraphList.Edge edge : graph.getNeighbors(u)) {
int v = edge.destination;
int weight = edge.weight;
if (!inMST[v] && weight < key[v]) {
key[v] = weight;
parent[v] = u;
pq.offer(new Node(v, key[v]));
}
}
}
return mstWeight;
}
}
4.2 Kruskal算法
public class Kruskal {
static class Edge implements Comparable<Edge> {
int src, dest, weight;
Edge(int src, int dest, int weight) {
this.src = src;
this.dest = dest;
this.weight = weight;
}
public int compareTo(Edge other) {
return this.weight - other.weight;
}
}
static class UnionFind {
int[] parent, rank;
UnionFind(int n) {
parent = new int[n];
rank = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
if (rank[rootX] < rank[rootY]) {
parent[rootX] = rootY;
} else if (rank[rootX] > rank[rootY]) {
parent[rootY] = rootX;
} else {
parent[rootY] = rootX;
rank[rootX]++;
}
}
}
}
public static int kruskalMST(List<Edge> edges, int vertexCount) {
Collections.sort(edges);
UnionFind uf = new UnionFind(vertexCount);
int mstWeight = 0;
int edgesAdded = 0;
for (Edge edge : edges) {
if (edgesAdded == vertexCount - 1) break;
int rootSrc = uf.find(edge.src);
int rootDest = uf.find(edge.dest);
if (rootSrc != rootDest) {
uf.union(edge.src, edge.dest);
mstWeight += edge.weight;
edgesAdded++;
}
}
return mstWeight;
}
}
五、图算法的应用场景
5.1 社交网络分析
public class SocialNetworkAnalyzer {
private GraphList socialGraph;
public SocialNetworkAnalyzer(int userCount) {
socialGraph = new GraphList(userCount);
}
// 添加好友关系
public void addFriendship(int user1, int user2) {
socialGraph.addEdge(user1, user2, 1); // 权重为1表示一度关系
socialGraph.addEdge(user2, user1, 1);
}
// 查找共同好友
public List<Integer> findMutualFriends(int user1, int user2) {
Set<Integer> friends1 = new HashSet<>();
for (GraphList.Edge edge : socialGraph.getNeighbors(user1)) {
friends1.add(edge.destination);
}
List<Integer> mutualFriends = new ArrayList<>();
for (GraphList.Edge edge : socialGraph.getNeighbors(user2)) {
if (friends1.contains(edge.destination)) {
mutualFriends.add(edge.destination);
}
}
return mutualFriends;
}
// 计算两个人之间的最短社交距离
public int findSocialDistance(int user1, int user2) {
int[] distances = BFS.shortestPathUnweighted(socialGraph, user1);
return distances[user2];
}
// 寻找社交影响力最大的人(度中心性)
public int findMostInfluentialUser() {
int maxDegree = -1;
int mostInfluential = -1;
for (int i = 0; i < socialGraph.vertexCount; i++) {
int degree = socialGraph.getNeighbors(i).size();
if (degree > maxDegree) {
maxDegree = degree;
mostInfluential = i;
}
}
return mostInfluential;
}
}
5.2 路径规划与导航系统
public class NavigationSystem {
private GraphList roadNetwork;
private Map<Integer, String> locationNames;
public NavigationSystem(int locationCount) {
roadNetwork = new GraphList(locationCount);
locationNames = new HashMap<>();
}
public void addRoad(int from, int to, int distance, String roadName) {
roadNetwork.addEdge(from, to, distance);
roadNetwork.addEdge(to, from, distance); // 双向道路
}
public void setLocationName(int locationId, String name) {
locationNames.put(locationId, name);
}
// 查找最短路径
public NavigationResult findShortestPath(int start, int end) {
int[] distances = Dijkstra.dijkstra(roadNetwork, start);
int[] previous = new int[roadNetwork.vertexCount];
Arrays.fill(previous, -1);
// 这里需要修改Dijkstra算法来记录路径
// 实际实现中需要在Dijkstra算法中添加previous数组记录
int distance = distances[end];
List<Integer> path = reconstructPath(previous, start, end);
List<String> pathNames = new ArrayList<>();
for (int location : path) {
pathNames.add(locationNames.getOrDefault(location, "位置" + location));
}
return new NavigationResult(pathNames, distance);
}
// 查找多个目的地的最优路径(旅行商问题近似解)
public List<Integer> findOptimalRoute(int start, List<Integer> destinations) {
// 使用最近邻算法作为近似解
List<Integer> route = new ArrayList<>();
route.add(start);
Set<Integer> unvisited = new HashSet<>(destinations);
int current = start;
while (!unvisited.isEmpty()) {
int nearest = findNearestLocation(current, unvisited);
route.add(nearest);
unvisited.remove(nearest);
current = nearest;
}
return route;
}
private int findNearestLocation(int from, Set<Integer> destinations) {
int[] distances = Dijkstra.dijkstra(roadNetwork, from);
int minDistance = Integer.MAX_VALUE;
int nearest = -1;
for (int dest : destinations) {
if (distances[dest] < minDistance) {
minDistance = distances[dest];
nearest = dest;
}
}
return nearest;
}
static class NavigationResult {
List<String> path;
int totalDistance;
NavigationResult(List<String> path, int totalDistance) {
this.path = path;
this.totalDistance = totalDistance;
}
}
}
5.3 推荐系统
public class RecommendationSystem {
private GraphList userItemGraph; // 二分图:用户-物品交互图
private int userCount;
private int itemCount;
public RecommendationSystem(int userCount, int itemCount) {
this.userCount = userCount;
this.itemCount = itemCount;
this.userItemGraph = new GraphList(userCount + itemCount);
}
// 添加用户-物品交互(如购买、点击)
public void addInteraction(int userId, int itemId, int weight) {
int itemNodeId = userCount + itemId; // 物品节点的编号偏移
userItemGraph.addEdge(userId, itemNodeId, weight);
userItemGraph.addEdge(itemNodeId, userId, weight);
}
// 基于用户的协同过滤
public List<Integer> recommendForUser(int userId, int topK) {
// 查找相似用户
Map<Integer, Integer> userSimilarities = new HashMap<>();
// 获取目标用户交互过的物品
Set<Integer> targetUserItems = new HashSet<>();
for (GraphList.Edge edge : userItemGraph.getNeighbors(userId)) {
targetUserItems.add(edge.destination - userCount);
}
// 计算与其他用户的相似度
for (int otherUserId = 0; otherUserId < userCount; otherUserId++) {
if (otherUserId == userId) continue;
Set<Integer> otherUserItems = new HashSet<>();
for (GraphList.Edge edge : userItemGraph.getNeighbors(otherUserId)) {
otherUserItems.add(edge.destination - userCount);
}
// 计算Jaccard相似度
Set<Integer> intersection = new HashSet<>(targetUserItems);
intersection.retainAll(otherUserItems);
Set<Integer> union = new HashSet<>(targetUserItems);
union.addAll(otherUserItems);
double similarity = union.isEmpty() ? 0 :
(double) intersection.size() / union.size();
userSimilarities.put(otherUserId, (int) (similarity * 100));
}
// 根据相似用户的喜好推荐物品
Map<Integer, Integer> itemScores = new HashMap<>();
for (Map.Entry<Integer, Integer> entry : userSimilarities.entrySet()) {
int otherUserId = entry.getKey();
int similarity = entry.getValue();
for (GraphList.Edge edge : userItemGraph.getNeighbors(otherUserId)) {
int itemId = edge.destination - userCount;
if (!targetUserItems.contains(itemId)) { // 排除已交互的物品
itemScores.put(itemId, itemScores.getOrDefault(itemId, 0) +
similarity * edge.weight);
}
}
}
// 返回得分最高的物品
return itemScores.entrySet().stream()
.sorted(Map.Entry.<Integer, Integer>comparingByValue().reversed())
.limit(topK)
.map(Map.Entry::getKey)
.collect(Collectors.toList());
}
// 基于图的扩散算法(Personalized PageRank)
public List<Integer> recommendWithPageRank(int userId, int topK, double damping, int iterations) {
double[] ranks = new double[userCount + itemCount];
ranks[userId] = 1.0;
for (int i = 0; i < iterations; i++) {
double[] newRanks = new double[userCount + itemCount];
for (int node = 0; node < userCount + itemCount; node++) {
if (ranks[node] == 0) continue;
List<GraphList.Edge> neighbors = userItemGraph.getNeighbors(node);
if (neighbors.isEmpty()) {
newRanks[node] += ranks[node];
} else {
double transfer = damping * ranks[node] / neighbors.size();
for (GraphList.Edge edge : neighbors) {
newRanks[edge.destination] += transfer;
}
newRanks[node] += (1 - damping) * ranks[node];
}
}
ranks = newRanks;
}
// 只返回物品的排名(排除用户节点)
Map<Integer, Double> itemRanks = new HashMap<>();
for (int itemId = 0; itemId < itemCount; itemId++) {
int nodeId = userCount + itemId;
itemRanks.put(itemId, ranks[nodeId]);
}
return itemRanks.entrySet().stream()
.sorted(Map.Entry.<Integer, Double>comparingByValue().reversed())
.limit(topK)
.map(Map.Entry::getKey)
.collect(Collectors.toList());
}
}
六、性能分析与优化
6.1 算法复杂度比较
|
算法 |
时间复杂度 |
空间复杂度 |
适用场景 |
|
BFS |
O(V + E) |
O(V) |
未加权图最短路径、连通性检测 |
|
DFS |
O(V + E) |
O(V) |
拓扑排序、环检测、路径查找 |
|
Dijkstra |
O((V + E) log V) |
O(V) |
非负权重最短路径 |
|
Floyd-Warshall |
O(V³) |
O(V²) |
所有顶点对最短路径 |
|
Prim |
O((V + E) log V) |
O(V) |
最小生成树(稠密图) |
|
Kruskal |
O(E log E) |
O(V + E) |
最小生成树(稀疏图) |
6.2 优化技巧
- 使用合适的图表示法:
- 稠密图:使用邻接矩阵
- 稀疏图:使用邻接表
- 算法选择:
- 单源最短路径:Dijkstra(非负权重)、Bellman-Ford(可处理负权重)
- 所有顶点对最短路径:Floyd-Warshall(小规模图)、多次Dijkstra(大规模图)
- 数据结构优化:
- 使用优先队列优化Dijkstra和Prim算法
- 使用并查集优化Kruskal算法
- 并行计算:
- Floyd-Warshall等算法可以并行化处理
// 并行Floyd-Warshall示例
public static int[][] floydWarshallParallel(int[][] graph) {
int n = graph.length;
int[][] dist = new int[n][n];
// 初始化距离矩阵(同上)
// ...
// 并行处理
for (int k = 0; k < n; k++) {
final int kFinal = k;
IntStream.range(0, n).parallel().forEach(i -> {
for (int j = 0; j < n; j++) {
if (dist[i][kFinal] + dist[kFinal][j] < dist[i][j]) {
dist[i][j] = dist[i][kFinal] + dist[kFinal][j];
}
}
});
}
return dist;
}
总结
图结构是计算机科学中最通用和强大的数据结构之一,能够表示各种复杂的关系网络。从社交网络到交通系统,从推荐引擎到网络路由,图算法在现代计算中无处不在。
关键要点:
- 根据图的特点(稠密/稀疏、有权/无权、有向/无向)选择合适的表示方法和算法
- BFS和DFS是图算法的基础,掌握它们至关重要
- Dijkstra算法是解决单源最短路径问题的首选(非负权重)
- 最小生成树算法(Prim、Kruskal)在网络设计中有重要应用
- 图算法在社交网络分析、推荐系统、路径规划等领域有广泛应用
实践建议:
- 对于大规模图,优先使用邻接表表示法
- 使用优先队列等数据结构优化算法性能
- 考虑使用现成的图处理库(如JGraphT)用于生产环境
- 对于特别大的图,考虑使用分布式图处理系统(如Spark GraphX)
掌握图算法不仅能够解决复杂的实际问题,也是衡量程序员算法能力的重要标准。通过深入理解图的基本概念和算法原理,并结合实际应用场景,可以构建出高效、智能的系统解决方案。






















 961
961

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










