《数据之美》：数组的精妙世界与经典算法-优快云博客

一、数组：最简单却最重要的数据结构

1.1 数组的本质与特性

数组是计算机科学中最基本且最重要的数据结构之一，它是一组连续内存空间的集合，用于存储相同类型的元素。这种连续性使得数组具有独特的性能特征：

// 数组的声明和初始化
int[] numbers = new int[5]; // 固定长度数组
String[] names = {"Alice", "Bob", "Charlie"}; // 初始化时赋值
// 多维数组
int[][] matrix = new int[3][3]; // 3x3的二维数组

数组的核心特性：

随机访问：通过索引直接访问任何元素，时间复杂度为O(1)
内存连续：所有元素在内存中连续存储，缓存友好
固定大小：一旦创建，大小不可改变（在Java中）
类型安全：所有元素必须是相同类型

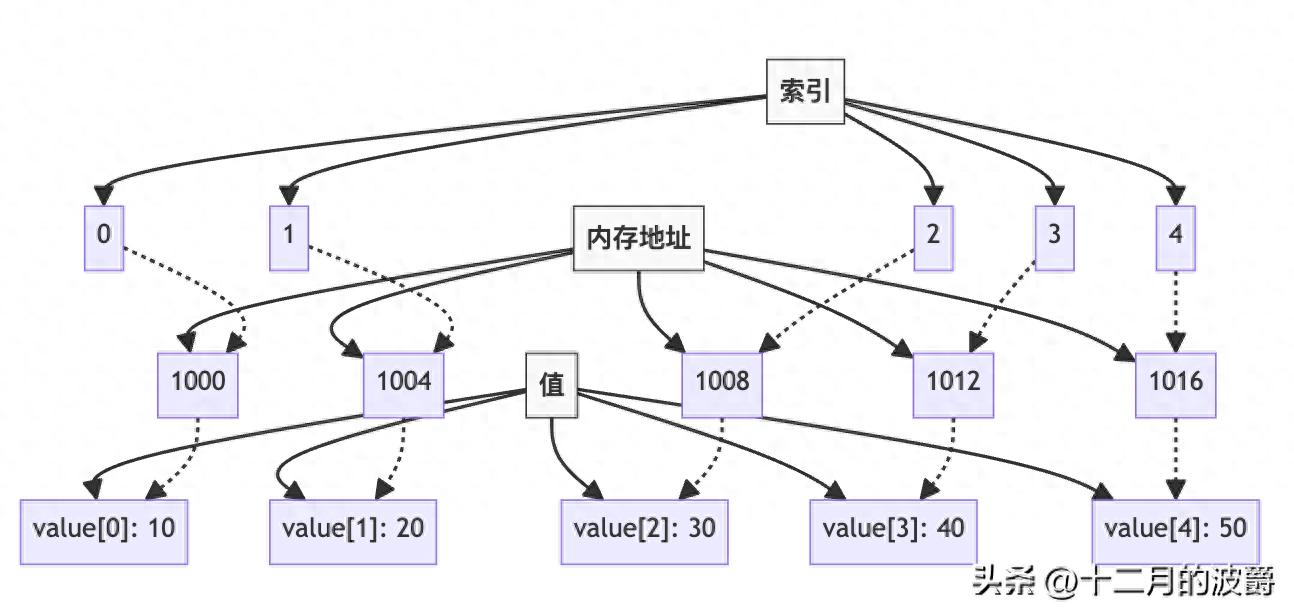
1.2 数组的内存表示

为了更好地理解数组的连续内存特性，让我们看一个直观的内存布局示意图：

二、排序算法：让数据有序的艺术

2.1 冒泡排序（Bubble Sort）

算法思想：重复遍历数组，比较相邻元素并交换，将最大元素"冒泡"到末尾。

public void bubbleSort(int[] arr) {
    int n = arr.length;
    for (int i = 0; i < n - 1; i++) {
        boolean swapped = false;
        for (int j = 0; j < n - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                // 交换元素
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
                swapped = true;
            }
        }
        // 如果没有发生交换，说明已经有序
        if (!swapped) break;
    }
}

时间复杂度：最好O(n)，平均O(n²)，最坏O(n²)
空间复杂度：O(1)
稳定性：稳定

2.2 选择排序（Selection Sort）

算法思想：每次从未排序部分选择最小元素，放到已排序部分的末尾。

public void selectionSort(int[] arr) {
    int n = arr.length;
    for (int i = 0; i < n - 1; i++) {
        int minIndex = i;
        for (int j = i + 1; j < n; j++) {
            if (arr[j] < arr[minIndex]) {
                minIndex = j;
            }
        }
        // 交换找到的最小元素
        int temp = arr[minIndex];
        arr[minIndex] = arr[i];
        arr[i] = temp;
    }
}

时间复杂度：始终为O(n²)
空间复杂度：O(1)
稳定性：不稳定

2.3 插入排序（Insertion Sort）

算法思想：将每个元素插入到已排序部分的正确位置。

public void insertionSort(int[] arr) {
    int n = arr.length;
    for (int i = 1; i < n; i++) {
        int key = arr[i];
        int j = i - 1;
        
        // 将比key大的元素向后移动
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = key;
    }
}

时间复杂度：最好O(n)，平均O(n²)，最坏O(n²)
空间复杂度：O(1)
稳定性：稳定

2.4 快速排序（Quick Sort）

算法思想：分治策略，选择一个基准元素，将数组分为两部分，递归排序。

public void quickSort(int[] arr, int low, int high) {
    if (low < high) {
        // 分区操作，返回基准元素的正确位置
        int pi = partition(arr, low, high);
        
        // 递归排序基准元素前后的子数组
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}
private int partition(int[] arr, int low, int high) {
    int pivot = arr[high]; // 选择最后一个元素作为基准
    int i = low - 1; // 较小元素的索引
    
    for (int j = low; j < high; j++) {
        // 如果当前元素小于等于基准
        if (arr[j] <= pivot) {
            i++;
            // 交换arr[i]和arr[j]
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }
    
    // 将基准元素放到正确位置
    int temp = arr[i + 1];
    arr[i + 1] = arr[high];
    arr[high] = temp;
    
    return i + 1;
}

时间复杂度：最好O(n log n)，平均O(n log n)，最坏O(n²)
空间复杂度：O(log n)
稳定性：不稳定

三、二分查找：高效的搜索算法

3.1 基本二分查找

前提条件：数组必须是有序的

算法思想：通过不断将搜索区间减半来快速定位目标元素。

public int binarySearch(int[] arr, int target) {
    int left = 0;
    int right = arr.length - 1;
    
    while (left <= right) {
        int mid = left + (right - left) / 2; // 防止整数溢出
        
        if (arr[mid] == target) {
            return mid; // 找到目标，返回索引
        } else if (arr[mid] < target) {
            left = mid + 1; // 目标在右半部分
        } else {
            right = mid - 1; // 目标在左半部分
        }
    }
    
    return -1; // 未找到目标
}

3.2 二分查找的变种

查找第一个等于目标值的元素：

public int binarySearchFirst(int[] arr, int target) {
    int left = 0;
    int right = arr.length - 1;
    int result = -1;
    
    while (left <= right) {
        int mid = left + (right - left) / 2;
        
        if (arr[mid] == target) {
            result = mid; // 记录位置，继续在左半部分查找
            right = mid - 1;
        } else if (arr[mid] < target) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }
    
    return result;
}

查找最后一个等于目标值的元素：

public int binarySearchLast(int[] arr, int target) {
    int left = 0;
    int right = arr.length - 1;
    int result = -1;
    
    while (left <= right) {
        int mid = left + (right - left) / 2;
        
        if (arr[mid] == target) {
            result = mid; // 记录位置，继续在右半部分查找
            left = mid + 1;
        } else if (arr[mid] < target) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }
    
    return result;
}

四、算法性能对比与实践建议

4.1 排序算法性能比较

算法	最好情况	平均情况	最坏情况	空间复杂度	稳定性	适用场景
冒泡排序	O(n)	O(n²)	O(n²)	O(1)	稳定	小规模数据或基本有序数据
选择排序	O(n²)	O(n²)	O(n²)	O(1)	不稳定	小规模数据，写操作代价高时
插入排序	O(n)	O(n²)	O(n²)	O(1)	稳定	小规模或基本有序数据
快速排序	O(n log n)	O(n log n)	O(n²)	O(log n)	不稳定	大规模数据，通用排序

4.2 实际开发建议

小规模数据（n < 50）：选择插入排序，常数因子小，实际性能好
中等规模数据：考虑使用快速排序，性能较好
大规模数据：使用Java内置的Arrays.sort()，它根据数据特征选择最优算法
搜索操作：对于静态数据，先排序后使用二分查找
内存限制：当内存紧张时，选择原地排序算法（如上述所有算法）

// Java内置排序方法的使用
int[] arr = {5, 2, 8, 1, 9};
Arrays.sort(arr); // 使用优化的快速排序
// 对对象数组排序
String[] names = {"John", "Alice", "Bob"};
Arrays.sort(names); // 使用归并排序（稳定）