《数据之美》：栈的精妙世界与算法实践

最新推荐文章于 2025-12-05 17:52:33 发布

原创最新推荐文章于 2025-12-05 17:52:33 发布 · 961 阅读

25 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构 #java

数据之美专栏收录该内容

7 篇文章

订阅专栏

一、栈：后进先出的线性数据结构

1.1 栈的基本概念与特性

栈（Stack）是一种后进先出（Last-In-First-Out, LIFO）的线性数据结构，只允许在固定的一端（栈顶）进行插入和删除操作。这种特性使得栈在各种计算机科学场景中有着广泛的应用。

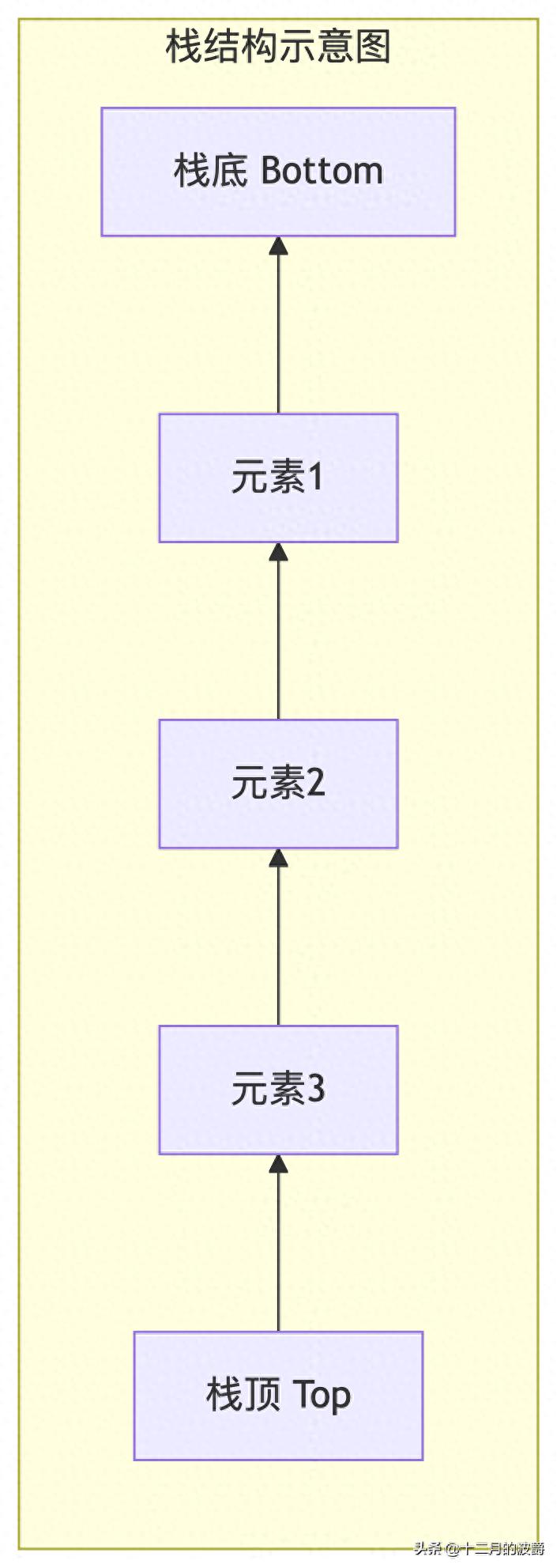
栈的核心操作：

push(压栈)：将元素添加到栈顶
pop(弹栈)：移除并返回栈顶元素
peek(查看)：返回栈顶元素但不移除
isEmpty：检查栈是否为空
size：返回栈中元素数量

1.2 栈的ADT（抽象数据类型）定义

public interface Stack<T> {
    void push(T element);    // 压栈操作
    T pop();                 // 弹栈操作
    T peek();                // 查看栈顶元素
    boolean isEmpty();       // 判断栈是否为空
    int size();              // 获取栈大小
}

二、栈的实现方式

2.1 基于数组的实现

public class ArrayStack<T> implements Stack<T> {
    private static final int DEFAULT_CAPACITY = 10;
    private T[] elements;
    private int top; // 栈顶指针
    
    public ArrayStack() {
        this(DEFAULT_CAPACITY);
    }
    
    @SuppressWarnings("unchecked")
    public ArrayStack(int capacity) {
        elements = (T[]) new Object[capacity];
        top = -1;
    }
    
    @Override
    public void push(T element) {
        if (top == elements.length - 1) {
            resize(2 * elements.length); // 动态扩容
        }
        elements[++top] = element;
    }
    
    @Override
    public T pop() {
        if (isEmpty()) {
            throw new EmptyStackException();
        }
        T element = elements[top];
        elements[top--] = null; // 避免内存泄漏
        
        // 缩容机制
        if (top > 0 && top == elements.length / 4) {
            resize(elements.length / 2);
        }
        return element;
    }
    
    @Override
    public T peek() {
        if (isEmpty()) {
            throw new EmptyStackException();
        }
        return elements[top];
    }
    
    @Override
    public boolean isEmpty() {
        return top == -1;
    }
    
    @Override
    public int size() {
        return top + 1;
    }
    
    private void resize(int newCapacity) {
        @SuppressWarnings("unchecked")
        T[] newElements = (T[]) new Object[newCapacity];
        for (int i = 0; i <= top; i++) {
            newElements[i] = elements[i];
        }
        elements = newElements;
    }
}

2.2 基于链表的实现

public class LinkedStack<T> implements Stack<T> {
    private static class Node<T> {
        T data;
        Node<T> next;
        
        Node(T data) {
            this.data = data;
        }
    }
    
    private Node<T> top;
    private int size;
    
    public LinkedStack() {
        top = null;
        size = 0;
    }
    
    @Override
    public void push(T element) {
        Node<T> newNode = new Node<>(element);
        newNode.next = top;
        top = newNode;
        size++;
    }
    
    @Override
    public T pop() {
        if (isEmpty()) {
            throw new EmptyStackException();
        }
        T element = top.data;
        top = top.next;
        size--;
        return element;
    }
    
    @Override
    public T peek() {
        if (isEmpty()) {
            throw new EmptyStackException();
        }
        return top.data;
    }
    
    @Override
    public boolean isEmpty() {
        return top == null;
    }
    
    @Override
    public int size() {
        return size;
    }
}

2.3 两种实现方式的对比

特性	数组实现	链表实现
时间复杂度	所有操作O(1)	所有操作O(1)
空间复杂度	需要预先分配空间	动态分配，无空间浪费
内存使用	可能有空间浪费	每个元素需要额外指针空间
扩容成本	需要复制整个数组	无需扩容
适用场景	元素数量可预测	元素数量变化大

三、栈的核心算法与应用

3.1 括号匹配问题

问题描述：检查字符串中的括号是否正确匹配。

public boolean isValidParentheses(String s) {
    Stack<Character> stack = new ArrayStack<>();
    
    for (char c : s.toCharArray()) {
        if (c == '(' || c == '[' || c == '{') {
            stack.push(c);
        } else if (c == ')' || c == ']' || c == '}') {
            if (stack.isEmpty()) {
                return false;
            }
            char top = stack.pop();
            if ((c == ')' && top != '(') ||
                (c == ']' && top != '[') ||
                (c == '}' && top != '{')) {
                return false;
            }
        }
    }
    
    return stack.isEmpty();
}
// 测试示例
System.out.println(isValidParentheses("()[]{}")); // true
System.out.println(isValidParentheses("([)]"));   // false

3.2 表达式求值

中缀表达式转后缀表达式（逆波兰表达式）：

public String infixToPostfix(String infix) {
    StringBuilder postfix = new StringBuilder();
    Stack<Character> stack = new ArrayStack<>();
    
    for (char c : infix.toCharArray()) {
        if (Character.isDigit(c)) {
            postfix.append(c).append(' ');
        } else if (c == '(') {
            stack.push(c);
        } else if (c == ')') {
            while (!stack.isEmpty() && stack.peek() != '(') {
                postfix.append(stack.pop()).append(' ');
            }
            stack.pop(); // 弹出 '('
        } else if (isOperator(c)) {
            while (!stack.isEmpty() && precedence(stack.peek()) >= precedence(c)) {
                postfix.append(stack.pop()).append(' ');
            }
            stack.push(c);
        }
    }
    
    while (!stack.isEmpty()) {
        postfix.append(stack.pop()).append(' ');
    }
    
    return postfix.toString().trim();
}
private boolean isOperator(char c) {
    return c == '+' || c == '-' || c == '*' || c == '/';
}
private int precedence(char operator) {
    switch (operator) {
        case '+':
        case '-':
            return 1;
        case '*':
        case '/':
            return 2;
        default:
            return 0;
    }
}

后缀表达式求值：

public int evaluatePostfix(String postfix) {
    Stack<Integer> stack = new ArrayStack<>();
    String[] tokens = postfix.split("\\s+");
    
    for (String token : tokens) {
        if (token.matches("\\d+")) {
            stack.push(Integer.parseInt(token));
        } else {
            int operand2 = stack.pop();
            int operand1 = stack.pop();
            int result = applyOperation(token.charAt(0), operand1, operand2);
            stack.push(result);
        }
    }
    
    return stack.pop();
}
private int applyOperation(char operator, int a, int b) {
    switch (operator) {
        case '+': return a + b;
        case '-': return a - b;
        case '*': return a * b;
        case '/': 
            if (b == 0) throw new ArithmeticException("Division by zero");
            return a / b;
        default: throw new IllegalArgumentException("Invalid operator: " + operator);
    }
}

3.3 栈在递归中的应用

递归的栈模拟 - 以斐波那契数列为例：

// 递归实现
public int fibonacciRecursive(int n) {
    if (n <= 1) return n;
    return fibonacciRecursive(n - 1) + fibonacciRecursive(n - 2);
}
// 栈模拟递归实现
public int fibonacciIterative(int n) {
    if (n <= 1) return n;
    
    Stack<Integer> stack = new ArrayStack<>();
    stack.push(n);
    int result = 0;
    
    while (!stack.isEmpty()) {
        int current = stack.pop();
        
        if (current <= 1) {
            result += current;
        } else {
            stack.push(current - 1);
            stack.push(current - 2);
        }
    }
    
    return result;
}

3.4 单调栈算法

下一个更大元素问题：

public int[] nextGreaterElement(int[] nums) {
    int[] result = new int[nums.length];
    Arrays.fill(result, -1);
    Stack<Integer> stack = new ArrayStack<>();
    
    for (int i = 0; i < nums.length; i++) {
        while (!stack.isEmpty() && nums[i] > nums[stack.peek()]) {
            int index = stack.pop();
            result[index] = nums[i];
        }
        stack.push(i);
    }
    
    return result;
}
// 测试示例
int[] nums = {2, 1, 2, 4, 3};
int[] result = nextGreaterElement(nums);
// 结果: [4, 2, 4, -1, -1]

四、栈的实际应用场景

4.1 浏览器历史记录

public class BrowserHistory {
    private Stack<String> backStack;
    private Stack<String> forwardStack;
    private String currentPage;
    
    public BrowserHistory(String homepage) {
        backStack = new ArrayStack<>();
        forwardStack = new ArrayStack<>();
        currentPage = homepage;
    }
    
    public void visit(String url) {
        backStack.push(currentPage);
        currentPage = url;
        forwardStack = new ArrayStack<>(); // 清空前向历史
        System.out.println("Visiting: " + url);
    }
    
    public String back(int steps) {
        while (steps > 0 && !backStack.isEmpty()) {
            forwardStack.push(currentPage);
            currentPage = backStack.pop();
            steps--;
        }
        System.out.println("Back to: " + currentPage);
        return currentPage;
    }
    
    public String forward(int steps) {
        while (steps > 0 && !forwardStack.isEmpty()) {
            backStack.push(currentPage);
            currentPage = forwardStack.pop();
            steps--;
        }
        System.out.println("Forward to: " + currentPage);
        return currentPage;
    }
    
    public String getCurrentPage() {
        return currentPage;
    }
}
// 使用示例
BrowserHistory browser = new BrowserHistory("homepage.com");
browser.visit("google.com");
browser.visit("github.com");
browser.back(1); // 返回 google.com
browser.forward(1); // 前进到 github.com

4.2 文本编辑器中的撤销/重做功能

public class TextEditor {
    private Stack<String> undoStack;
    private Stack<String> redoStack;
    private StringBuilder content;
    
    public TextEditor() {
        undoStack = new ArrayStack<>();
        redoStack = new ArrayStack<>();
        content = new StringBuilder();
    }
    
    public void type(String text) {
        undoStack.push(content.toString());
        content.append(text);
        redoStack.clear(); // 新的输入清除重做历史
        System.out.println("Typed: " + text);
    }
    
    public void undo() {
        if (!undoStack.isEmpty()) {
            redoStack.push(content.toString());
            content = new StringBuilder(undoStack.pop());
            System.out.println("Undo to: " + content.toString());
        }
    }
    
    public void redo() {
        if (!redoStack.isEmpty()) {
            undoStack.push(content.toString());
            content = new StringBuilder(redoStack.pop());
            System.out.println("Redo to: " + content.toString());
        }
    }
    
    public String getContent() {
        return content.toString();
    }
}

4.3 函数调用栈

public class FunctionCallStack {
    private static void functionA() {
        System.out.println("进入函数A");
        functionB();
        System.out.println("离开函数A");
    }
    
    private static void functionB() {
        System.out.println("进入函数B");
        functionC();
        System.out.println("离开函数B");
    }
    
    private static void functionC() {
        System.out.println("进入函数C");
        System.out.println("执行函数C的操作");
        System.out.println("离开函数C");
    }
    
    public static void main(String[] args) {
        System.out.println("程序开始执行");
        functionA();
        System.out.println("程序执行结束");
    }
}

输出结果：

程序开始执行
进入函数A
进入函数B
进入函数C
执行函数C的操作
离开函数C
离开函数B
离开函数A
程序执行结束

4.4 深度优先搜索（DFS）

public class GraphDFS {
    private Map<Integer, List<Integer>> graph;
    
    public GraphDFS() {
        graph = new HashMap<>();
    }
    
    public void addEdge(int u, int v) {
        graph.putIfAbsent(u, new ArrayList<>());
        graph.get(u).add(v);
    }
    
    public void dfs(int start) {
        Set<Integer> visited = new HashSet<>();
        Stack<Integer> stack = new ArrayStack<>();
        
        stack.push(start);
        
        while (!stack.isEmpty()) {
            int node = stack.pop();
            
            if (!visited.contains(node)) {
                System.out.print(node + " ");
                visited.add(node);
                
                if (graph.containsKey(node)) {
                    // 逆序压栈以保证正常的遍历顺序
                    List<Integer> neighbors = graph.get(node);
                    for (int i = neighbors.size() - 1; i >= 0; i--) {
                        int neighbor = neighbors.get(i);
                        if (!visited.contains(neighbor)) {
                            stack.push(neighbor);
                        }
                    }
                }
            }
        }
    }
}
// 使用示例
GraphDFS graph = new GraphDFS();
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 3);
graph.addEdge(2, 4);
graph.dfs(0); // 输出: 0 2 4 1 3

五、栈的进阶应用与最佳实践

5.1 最小栈实现

支持O(1)时间复杂度获取最小元素的栈：

public class MinStack {
    private Stack<Integer> mainStack;
    private Stack<Integer> minStack;
    
    public MinStack() {
        mainStack = new ArrayStack<>();
        minStack = new ArrayStack<>();
    }
    
    public void push(int x) {
        mainStack.push(x);
        if (minStack.isEmpty() || x <= minStack.peek()) {
            minStack.push(x);
        }
    }
    
    public int pop() {
        int value = mainStack.pop();
        if (value == minStack.peek()) {
            minStack.pop();
        }
        return value;
    }
    
    public int top() {
        return mainStack.peek();
    }
    
    public int getMin() {
        return minStack.peek();
    }
}

5.2 栈的线程安全实现

public class ThreadSafeStack<T> implements Stack<T> {
    private final Stack<T> stack;
    private final ReentrantLock lock;
    
    public ThreadSafeStack() {
        stack = new LinkedStack<>();
        lock = new ReentrantLock();
    }
    
    @Override
    public void push(T element) {
        lock.lock();
        try {
            stack.push(element);
        } finally {
            lock.unlock();
        }
    }
    
    @Override
    public T pop() {
        lock.lock();
        try {
            return stack.pop();
        } finally {
            lock.unlock();
        }
    }
    
    // 其他方法的实现类似...
}

六、总结与最佳实践

6.1 栈的适用场景总结

括号匹配和语法检查：编译器、表达式求值
函数调用和递归：程序执行栈、DFS遍历
撤销/重做功能：文本编辑器、图形应用
浏览历史：浏览器、移动应用
算法应用：单调栈、表达式求值

6.2 最佳实践建议

选择正确的实现方式：
使用数组实现当元素数量可预测时
使用链表实现当元素数量变化较大时
使用Java内置的Stack类或Deque接口
注意栈溢出：
递归深度过大时考虑迭代实现
使用显式栈替代深层递归
线程安全考虑：
多线程环境下使用同步栈实现
考虑使用ConcurrentLinkedDeque等并发集合
内存管理：
及时释放不再使用的栈引用
监控栈的大小，避免内存泄漏

// Java内置栈的使用
import java.util.Stack;
public class JavaBuiltInStackExample {
    public static void main(String[] args) {
        Stack<Integer> stack = new Stack<>();
        
        // 压栈操作
        stack.push(1);
        stack.push(2);
        stack.push(3);
        
        // 查看栈顶元素
        System.out.println("Top element: " + stack.peek()); // 3
        
        // 弹栈操作
        while (!stack.isEmpty()) {
            System.out.println("Popped: " + stack.pop());
        }
        // 输出: 3, 2, 1
    }
}

栈作为一种基础而强大的数据结构，在计算机科学的各个领域都有着广泛的应用。掌握栈的原理和实现，理解其在不同场景下的应用，是每个Java开发者必备的技能。通过合理的栈结构选择和应用，可以编写出更高效、更健壮的程序。