前言:
快速排序(Quick Sort)是由英国计算机科学家 Tony Hoare 在1959年发明的,是一种基于分治法 (Divide and Conquer) 的策略,其核心思想是将复杂问题分解为多个子问题,通过逐个解决这些子问题来实现整体排序。

一、快速排序的思想
快速排序的核心思想:
①分解:选择基准,将数组分成两个子数组 (核心思想)
②解决:递归排序两个子数组
③合并:由于是原地排序,不需要合并步骤
快速排序的关键操作 : 分区(Partition)
选定一个基准值,根据基准值将数组分为两个子数组使得: [ left , keyi - 1 ] keyi [ keyi + 1 , right]
①所有小于基准的元素在基准左侧
②所有大于基准的元素在基准右侧
③基准元素在到达其最终排序位置后,将保持固定不再移动
快速排序的核心递归实现
递归的思路为:
①左子数组 (不包含基准值) 重复上述操作,选定一个基准值,使得基准元素达到其最终位置
②右子数组 (不包含基准值) 重复上述操作,选定一个基准值,使得基准元素达到其最终位置
③递归的边界条件:直到数组不可再进行分为左右子数组,即数组只含有一个元素。
直观逻辑展示:哨兵与分队 💂♂️
想象一下这样的场景,操场上有一排高矮不一的学生,老师要求大家按身高排队,快速排序的思路是这样做:
①选队长(找基准 Pivot):老师随便拉出一个同学(通常选队伍第一个),说:“你是基准 ( 队长 ) !站在中间!”
②站队(分区 Partition)老师对剩下的人说:“比队长矮的,统统站到队长左边去! 比队长高的,统统站到队长右边去!”
③递归(分治):现在队长归位了,老师把左边那一堆人看作一个小队,右边看作一个小队,分别重复上面的步骤,直到每个小队只剩一个人为止。
二、快速排序的工作流程
快速排序的精妙之处在于无需申请额外数组空间(避免内存浪费),而是直接在原数组中进行元素交换。
2.1 Hoare 分区法
我们可以采用(Hoare分区法)定义左右指针,以数组 [6, 1, 2, 7, 9, 3, 4, 5, 10, 8] 为例进行说明。
首先设立两个哨兵(指针):
-
哨兵 end(右指针):从最右边往左走,负责找比基准小的数。
-
哨兵 begin (左指针):从最左边往右走,负责找比基准大的数。
2.1.1Hoare 分区法原理:
哨兵begin 和 哨兵end 按照以下逻辑进行运作:
严格遵守“右边 end 先走,左边 begin 后走”
①当遇到比基准值小的数,哨兵end停下等待哨兵begin。
②哨兵begin开始从左往右寻找,寻找到比基准值大的数,哨兵begin停下脚步。
③当哨兵end寻找到比基准值小的数,哨兵begin寻找到比基准值大的数,交换一下哨兵begin 和 哨兵end寻找到的值,进行下一轮寻找。
④当哨兵end与哨兵begin相遇时,搜索过程结束,此时相遇的位置即为基准值所在位置。将基准值放入该位置后,本轮排序完成。
Hoare分区法动图展示:

2.1.2Hoare 分区法演示流程:
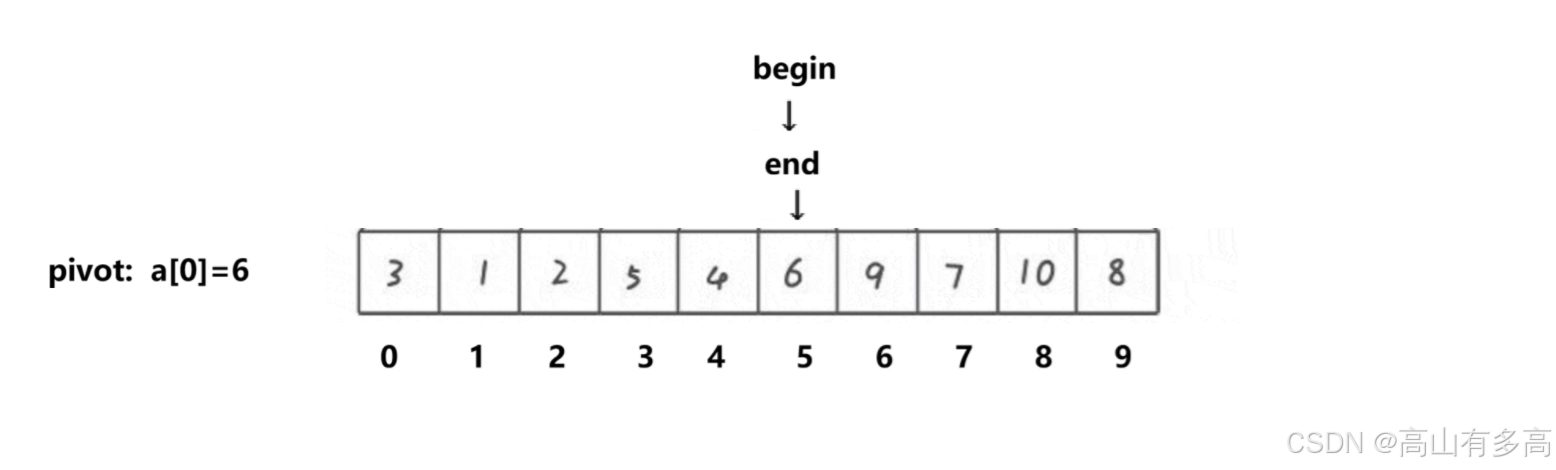
初始状态:
数组:
[6, 1, 2, 7, 9, 3, 4, 5, 10, 8]
索引:[0 1 2 3 4 5 6 7 8 9]基准 (Pivot):
6(索引 0)begin (左指针):指向
6(索引 0)end (右指针):指向
8(索引 9)
第一轮探测:
end 先走(找比 6 小的):
8 (比6大) -> 10 (比6大) -> 5 (比5小,停!) 🛑
end停在索引 7 (数值 5)。begin 后走(找比 6 大的):
6 (相等) -> 1(比6小) -> 2 (比6小) -> 7 (比6大,停!) 🛑
begin停在索引 3 (数值 7)。交换:
begin和end还没相遇,交换 7 和 5。数组:
[6, 1, 2, 5, 9, 3, 4, 7, 10, 8]
索引:[0 1 2 3 4 5 6 7 8 9](此时 5 到了左边,7 到了右边,符合预期)
第二轮探测:
end 继续走(找比 6 小的):
7 (比6大) -> 4 (比6小,停!) 🛑
end停在索引 6 (数值 4)。begin 继续走(找比 6 大的):
9 (比6大,停!) 🛑
begin停在索引 4 (数值 9)。交换:
begin和end还没相遇,交换 9 和 4。数组:
[6, 1, 2, 5, 4, 3, 9, 7, 10, 8]
索引:[0 1 2 3 4 5 6 7 8 9]
第三轮探测 (关键时刻!⚠️) :
end 继续走(找比 6 小的):
9 (比6大) -> 3 (小!停!) 🛑
end停在索引 5 (数值 3)。begin 继续走(找比 6 大的):
4 (小,继续走) -> 3 (小,继续走) ... ... 撞到了
end!💥相遇了! 当
begin撞上end时,这一轮探测立刻结束。相遇点:索引 5 (数值 3)。
基准归位:
现在,
begin和end都指着 3,我们需要把基准值 6 和 相遇点的 3 交换。
交换
arr[0](6) 和 arr[5] (3)。最终结果:
[3, 1, 2, 5, 4, 6, 9, 7, 10, 8]
验证数组:
当前数组为:[3, 1, 2, 5, 4, 6, 9, 7, 10, 8],观察一下基准值 6 左右子数组
左边:
[3, 1, 2, 5, 4]—— 全部小于 6 ✔右边:
[9, 7, 10, 8]—— 全部大于 6 ✔
2.1.3Hoare 分区法常见问题 :
①基准值选择最左边时,为什么要严格遵守“右边 end 先走,左边 begin 后走” ?
核心原因:为了确保最后与基准值(Pivot)交换的那个数,一定小于等于基准值。
示例解释:
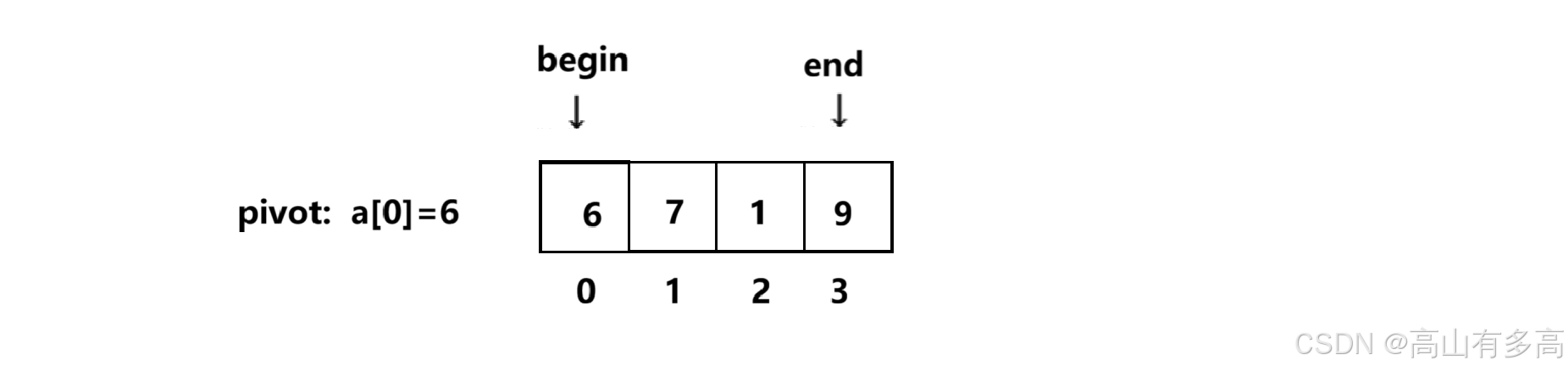
假设数组是:[6,7,1,9]
索引是: [0 1 2 3]
基准值(Pivot)是 6
Begin:指向
6(索引0)
End:指向
9(索引3)
❌ 反面教材:如果 Begin (左) 先走
第一轮探测:
Begin 出发(找大的):
Begin 从 6 往右走,遇到了 7。
7 > 6,符合条件。Begin 停在 7 这里。🛑
End 出发(找小的):
End 从 9 往左走,遇到了1。
1 < 6, 符合条件。End 停在1这里。🛑
交换:
begin和end还没相遇,交换 7 和 1。数组:
[6, 1 7, 9]
索引:[0 1 2 3]
第二轮探测:
begin出发(找大的):
begin 从 1 往右走,还没找到比 6 小的数,就直接撞到了 Begin(此时在 7)。
相遇!
基准归位(交换):
把基准值 6 和相遇点 7 交换。
数组变成了:
[7,1,6, 9]。
验证数组:
当前数组为:[7,1,6,9],观察一下基准值 6 左右子数组
左边:
[7,1]—— 不满足小于6 ❌右边:
[9]—— 全部大于 6 ✔
这样就导致了分区的混乱,左子区间不满足小于基准值pivot
✅ 正面教材:如果 End (右) 先走
初始状态(同上):
数组:
[6, 1,7, 9]索引: [0 1 2 3]
Pivot:
6Begin:指向
6(索引0)End:指向
9(索引2)

第一轮探测:
End 出发(找小的)
End 从 9 往左走,遇到了 1。
1 < 6, 符合条件。End 停在1这里。🛑
Begin 出发 (找大的)
Begin 从6往右走,遇到了7。
7 > 6,符合条件。 Begin 停在7这里。🛑
交换
begin和end还没相遇,交换 7 和 1。数组:
[6, 1 7, 9]
索引:[0 1 2 3]
第二轮探测:
End出发 (找小的)
End从7往左走,遇到了begin停止
begin和end相遇
基准归位(交换):
把基准值 6 和相遇点1交换。
数组变成了:
[1,6,7, 9]。
验证数组:
当前数组为:[1,6,7,9],观察一下基准值 6 左右子数组
左边:
[1]—— 不满足小于6 ✔右边:
[7,9]—— 全部大于 6 ✔
满足左子数组比基准值小,右子数组比基准值大。
②为什么哨兵begin 和 哨兵end 相遇的位置上的元素 比 pivot 基准值 小?
场景一:End 停下了,Begin 撞上去(begin相遇end)
End 为什么停下? 因为它找到了一个比基准小的数(这是它的职责)。
Begin 做了什么? Begin 还没找到大数,走着走着就撞到了 End。
结论:两人停在了 End 选中的那个位置。既然 End 选中了它,它必然小于基准值。✅
场景二:End 没停下,直接撞上了 Begin(end相遇begin)
这种情况发生时,Begin 停在哪里?Begin 只能停在上一轮刚刚交换过的位置(或者还没出发)。
上一轮发生了什么? Begin 找到了大数,End 找到了小数。两人交换了数值。
交换后 Begin 脚下是谁? 是刚刚从 End 那里换过来的小数!
End 这一轮做了什么? End 一路走没找到新的小数,直接撞到了 Begin 面前。
结论:End 撞上的其实是 Begin 手里攥着的上一轮的小数。所以该位置小于等于基准值。✅
2.1.4 代码实现
/*
int * a为待排序的数组
int left 为该数组的起始下标
int right 为该数组的末尾下标
*/
int PartionHoare(int *a,int left,int right)
{
//用keyi保存基准值的下标
int keyi = left;
//用begin指针从前往后找,right指针从后往前找
int begin = left, end = right;
while (begin < end)
{
//end从末尾向左找比a[keyi]小的元素
//保证begin<end
while (begin < end && a[end] >= a[keyi])
{
end--;
}
//begin从前往右找比a[keyi]大的元素
//保证begin<end
while (begin < end && a[begin] <= a[keyi])
{
begin++;
}
//交换当前a[begin] 和 a[end]
Swap(&a[begin], &a[end]);
}
//当begin 和 end 相遇时
//即begin==end
Swap(&a[keyi], &a[begin]);
//更小keyi
keyi = begin;
return keyi;
}
2.2 Dig-hole 挖坑分区法
我们可以采用(Dig-hole 挖坑分区法)左右指针,以数组 [6, 1, 2, 7, 9, 3, 4, 5, 10, 8] 为例进行说明。
首先设立两个哨兵(指针):
-
哨兵 end(右指针):从最右边往左走,负责找比基准小的数。
-
哨兵 begin (左指针):从最左边往右走,负责找比基准大的数。
2.2.1挖坑分区法原理 :
核心思想:一个萝卜一个坑,挖坑法的逻辑就像是挪动一个空位。
挖第一个坑:我们先把基准值(Pivot)拿出来,存到一个临时变量 key 里。这时候,基准值原来的位置就变成了一个 “坑” (Hole)。
填坑游戏:
①右边找小数填左坑:右指针 end 开始走,找到比 key 小的数,把它挖出来,填到左边的坑里,这时候,end 的位置变成了新坑。
②左边找大数填右坑:左指针 begin 开始走,找到比 key 大的数,把它挖出来,填到右边的坑里。这时候,begin 的位置变成了新坑。
③循环:左右交替填坑,直到 begin 和 end 相遇。
④基准归位:最后相遇的那个位置肯定是个坑,把最开始保存的 key 填进去。完美!
挖坑分区法动图展示:

2.2.2挖坑分区法演示流程:
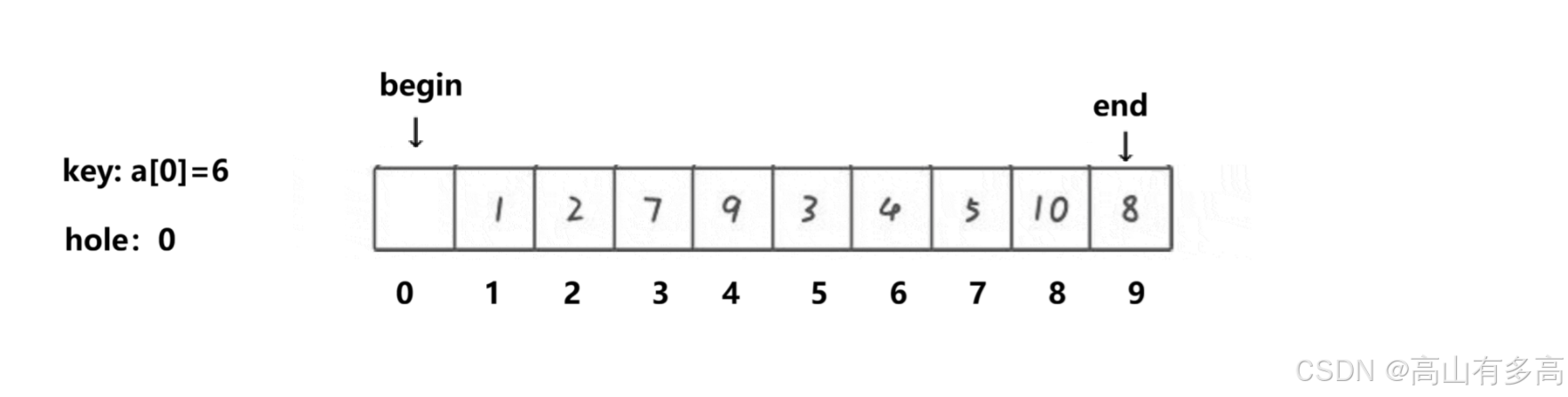
初始状态:
数组:
[6, 1, 2, 7, 9, 3, 4, 5, 10, 8]
索引:[0 1 2 3 4 5 6 7 8 9]基准 (Pivot):
6(索引 0)begin (左指针):指向
6(索引 0)end (右指针) :指向
8(索引 9)
当前状态:
数组:[ 🕳️, 1, 2, 7, 9, 3, 4, 5, 10, 8 ](key=6)
索引:[ 0 1 2 3 4 5 6 7 8 9]
坑的位置 hole:索引0
一、第一轮填坑
End (右边) 先行动:
目标:找比
key(6)小的数。8 (比key大) -> 10 (比key大) -> 5 (比key小,找到!)。
end停在索引 7。填坑操作:
把
end位置的 5 挖出来,填到 hole 的坑里。变化:索引 0 被填满了,
新坑的位置 hole:索引7。
数组:
[ 5, 1, 2, 7, 9, 3, 4, 🕳️, 10, 8 ]
索引: [ 0 1 2 3 4 5 6 7 8 9 ]Begin (左边) 行动:
目标:找比
key(6)大的数。此时
begin从索引 0 开始:5 (小) -> 1 (小) -> 2 (小) -> 7 (大!找到!)。
begin停在索引 3。填坑操作:
把
begin位置的 7 挖出来,填到end的坑里。变化:索引 7 被填满了。
新坑的位置 hole:索引3。
数组:
[ 5, 1, 2, 🕳️, 9, 3, 4, 7, 10, 8 ]
索引: [ 0 1 2 3 4 5 6 7 8 9 ]
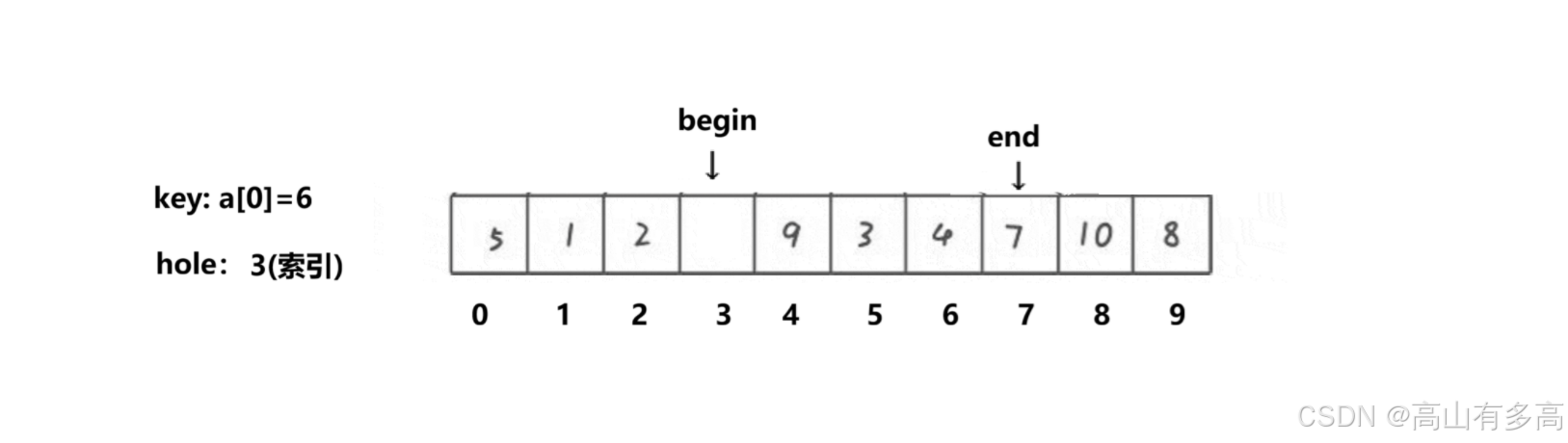
当前状态:
数组:[ 5, 1, 2, 🕳️, 9, 3, 4, 7, 10, 8 ](key=6)
索引: [ 0 1 2 3 4 5 6 7 8 9 ]
坑的位置 hole:索引3
二、第二轮填坑
End (右边) 继续行动:
从索引 7 往左走:7 (比key大) -> 4 (比key小,找到!)。
end停在索引 6。填坑操作:
把
end位置的 4 挖出来,填到 hole (索引 3)里。变化:索引 3 被填满
新坑的位置hole:索引 6 变新坑。
数组:
[ 5, 1, 2, 4, 9, 3, 🕳️, 7, 10, 8 ]
索引: [ 0 1 2 3 4 5 6 7 8 9 ]Begin (左边) 继续行动:
从索引 3 往右走:4 (比key小) -> 9 (比key大,找到!)。
begin停在索引 4。填坑操作:
把
begin位置的 9 挖出来,填到 hole(索引 6)里。变化:索引 6 被填满,
新坑的位置hole:索引 4 变新坑
数组:
[ 5, 1, 2, 4, 🕳️, 3, 9, 7, 10, 8 ]
索引: [ 0 1 2 3 4 5 6 7 8 9 ]
当前状态:
数组:[ 5, 1, 2, 🕳️, 9, 3, 4, 7, 10, 8 ](key=6)
索引: [ 0 1 2 3 4 5 6 7 8 9 ]
坑的位置 hole:索引4
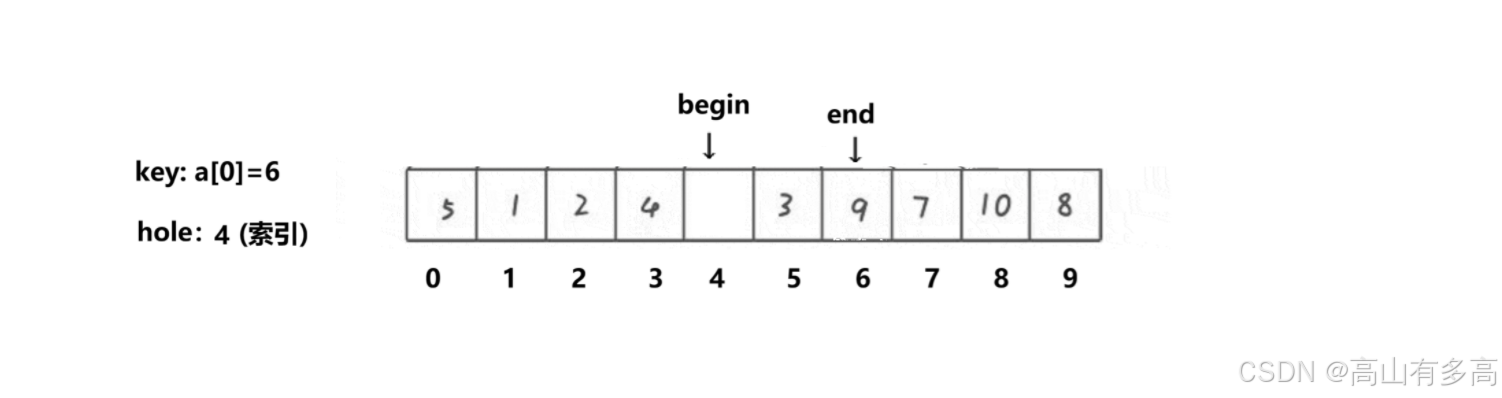
第三轮填坑(最后时刻!)
End (右边) 继续行动:
从索引 6 往左走:9 (比key大) -> 3 (比key小,找到!)。
end停在索引 5。填坑操作:
把
end位置的 3 挖出来,填到 hole(索引 4)里。变化:索引 4 被填满
新坑的位置hole:索引 5 变新坑。
数组:
[ 5, 1, 2, 4, 3, 🕳️, 9, 7, 10, 8 ]
索引: [ 0 1 2 3 4 5 6 7 8 9 ]Begin (左边) 继续行动:
从索引 4 往右走:3 (比key小)…… 撞到了 end!
begin也停在了索引 5。
此时 begin 和 end 相遇在索引 5,这里就是最后一个坑!
当前状态:
数组:
[ 5, 1, 2, 4, 3, 🕳️, 9, 7, 10, 8 ](key=6)
索引: [ 0 1 2 3 4 5 6 7 8 9 ]
当前坑位hole:索引5
终局:基准归位
手里一直攥着的 key = 6 终于可以放下了。把 6 填入最后的坑(索引 5)。
最终结果:
[ 5, 1, 2, 4, 3, 6, 9, 7, 10, 8 ]
✨ 验证一下
当前数组:
[ 5, 1, 2, 4, 3,6, 9, 7, 10, 8 ]
基准值左子数组:
5, 1, 2, 4, 3(全比 6 小 ✅)
基准值右子数组:
9, 7, 10, 8(全比 6 大 ✅)
2.2.3 代码实现
/*
int * a为待排序的数组
int left 为该数组的起始下标
int right 为该数组的末尾下标
*/
int PartionDigHole(int* a, int left, int right)
{
//基准值pivot: a[left] 存放到key中
int key= a[left];
//初始时坑在left位置
int hole = left;
//定义左指针:begin 右指针: end
int begin = left, end = right;
//当begin >= end退出循环
while (begin < end)
{
//最开始的坑在左边,需要用哨兵end从右往左去找一个较小的元素填坑
while (begin<end && a[end] >= key )
{
end--;
}
//填坑
a[hole] = a[end];
//产生新坑在end
hole = end;
//新产生的坑在end出,需要用哨兵begin从左往右去找一个较大的元素填坑
while (begin < end && a[begin] <= key )
{
begin++;
}
//填坑
a[hole] = a[begin];
//产生新坑在begin
hole = begin;
}
a[hole] = key;
//begin与end相遇
return hole;
}
2.3 Slow-fast 前后指针分区法
我们可以采用前后指针,以数组 [6, 1, 2, 7, 9, 3, 4, 5, 10, 8] 为例进行说明。
首先定义两个指针:
-
前指针 (prev):代表“小数区域”的边界,它的左边(包括它自己)全是比基准值小的数。
-
后指针 (cur):代表“探索者”,它负责在前面开路,去探测未知的数字。
2.3.1前后指针分区法
核心思想:推土机战术
基本规则如下:
①cur 一直往前走
②如果
cur遇到了比基准值小的数:
a.
prev往前走一步(扩大小数区域)。
b.如果
prev和cur不在同一个位置,就把他俩的值交换。(把这个新发现的小数,扔到prev的位置去)。
③如果 cur 遇到的是大数,直接跳过,不做任何事。
2.3.2 前后指针分区底层原理
1. 宏观地图:三个区域
在遍历的过程中,数组其实被这两个指针切分成了三个区域:
[ 基准 | 小数区域 | 大数区域 | 未知区域 ]
小数区域:从 left + 1 到
prev。大数区域:从
prev + 1到cur-1(也就是prev和cur中间夹着的部分)。未知区域:从
cur开始往后。
当
cur扫完整条街后,“未知区域”消失,只剩下左边的小数和右边的大数。
2.为什么cur指针 遇到大数“什么都不做”?🛑
当
cur遇到一个大数(比基准大):
操作:
cur继续往前走。发生了什么:
cur和prev之间的距离拉大了。逻辑:因为
cur刚刚跨过的这个大数,被自然地留在了 “大数区域”(prev和cur之间)。它本来就该待在那儿,所以不需要动它。
3. 为什么遇到小数要“prev 前进并交换”?
当
cur遇到一个小数(比基准小):这就出问题了!这个小数现在位于“大数区域”的后面,或者“未知区域”的开头,它必须回到“小数区域”去。
操作分解:
prev往前走一步 (prev + 1):
此时
prev从“小数区”的最后一个,跨进了 “大数区”的第一个。如果没有大数,相当于prev与cur紧挨,
prev就只是单纯往前挪了一格空位。交换
a[prev]和a[cur]:
把小数接回来:
cur位置的那个“新发现的小数”,被换到了prev的位置(也就是刚才那个大数的位置)。现在它安全地回到了“小数队”的末尾。把大数扔后面:
prev位置原本那个“大数”,被换到了cur的位置。这没关系,因为cur的位置本来就是“大数区”的延伸。这个大数只是往后挪了个位置,依然在“大数区”里。
前后指针分区法动图展示:

2.3.3前后指针分区法演示
1. Cur 遇到 1 (小)
判断:1 < 6,是小数!✅
操作:
Prev往前走一步 -> 到索引 1。
Prev和Cur都在索引 1,自己换自己(无变化)。
Cur继续走 -> 到索引 2。数组:
[6, 1, 2, 7, 9, 3, 4, 5, 10, 8]
2. Cur 遇到 2 (小)
判断:2 < 6,是小数!✅
操作:
Prev往前走一步 -> 到索引 2。
Prev和Cur都在索引 2,自己换自己。
Cur继续走 -> 到索引 3。数组:
[6, 1, 2, 7, 9, 3, 4, 5, 10, 8]
(目前为止,小数都在紧挨着的位置,还没出现空隙)
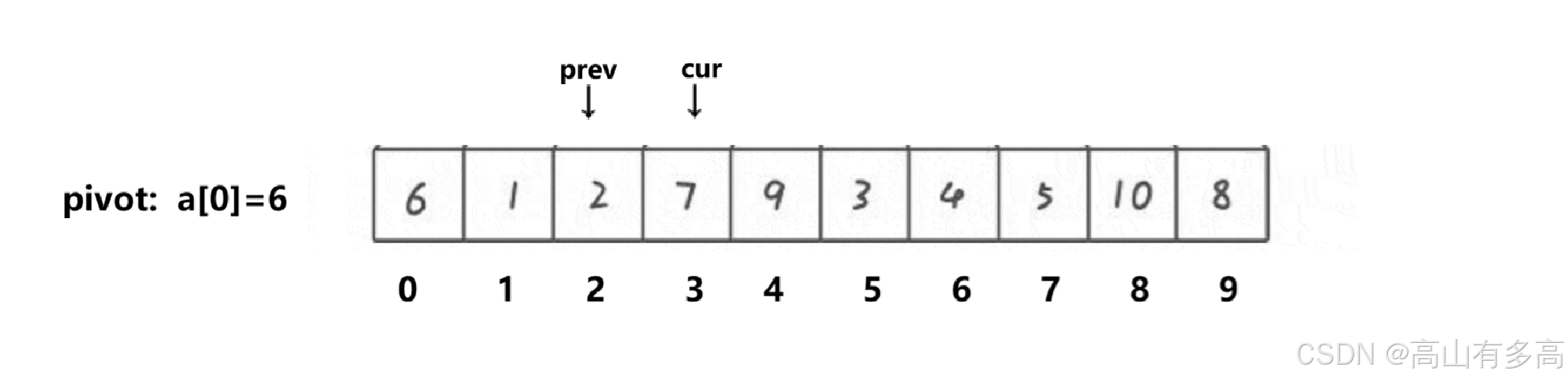
3. Cur 遇到 7 (大) 🛑
判断:7 > 6,是大数。
操作:什么都不做!
Prev停在索引 2 不动。
Cur继续走 -> 到索引 4。状态:
Prev=2,Cur=4。
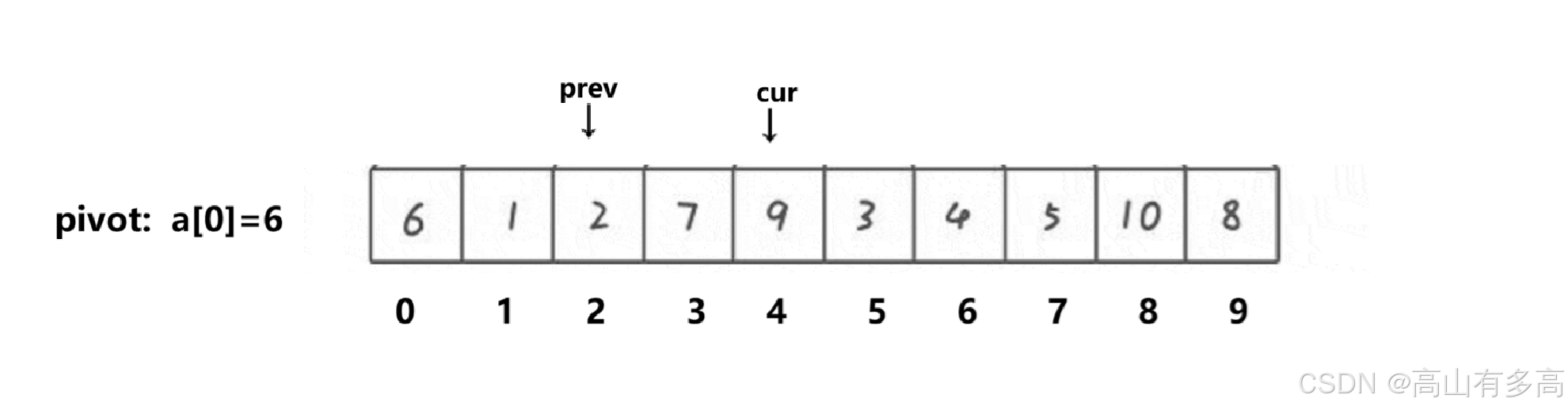
4. Cur 遇到 9 (大) 🛑
判断:9 > 6,是大数。
操作:什么都不做!
Prev停在索引 2 不动。
Cur继续走 -> 到索引 5。状态:
Prev=2,Cur=5。
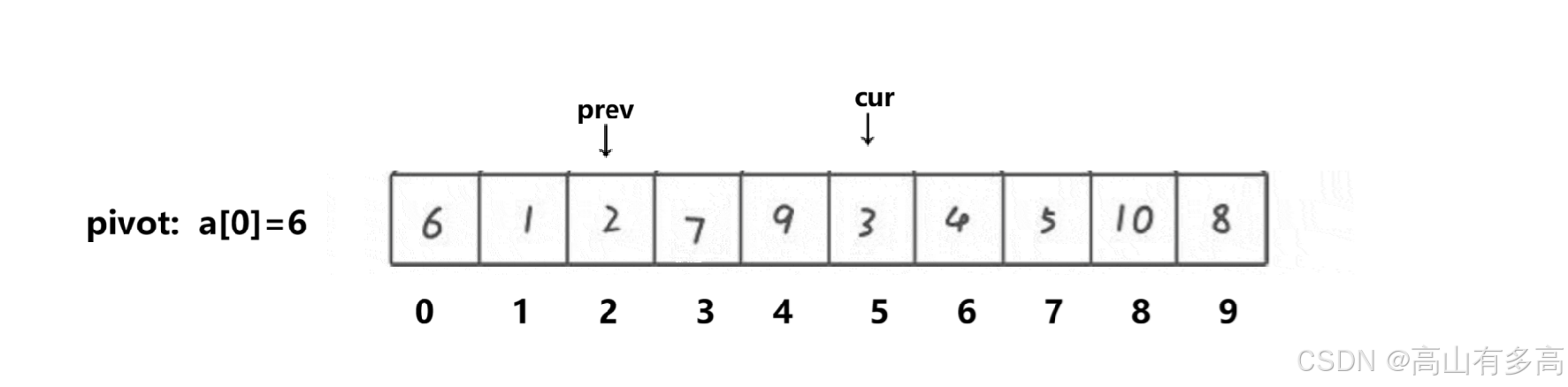
5. Cur 遇到 3 (小!关键时刻 ⚡️)
判断:3 < 6,是小数!✅
操作:
Prev往前走一步 -> 到索引 3 (此时arr[3]是大数 7)。交换
arr[Prev](7) 和arr[Cur](3)。
Cur继续走 -> 到索引 6。数组变身:
[6, 1, 2, 3, 9, 7, 4, 5, 10, 8]
(你看!小数 3 被拉进了 Prev 的队伍,大数 7 被甩到了后面)
6. Cur 遇到 4 (小) ⚡️
判断:4 < 6,是小数!✅
操作:
Prev往前走一步 -> 到索引 4 (此时arr[4]是大数 9)。交换
arr[Prev](9) 和arr[Cur](4)。
Cur继续走 -> 到索引 7。数组变身:
[6, 1, 2, 3, 4, 7, 9, 5, 10, 8]
7. Cur 遇到 5 (小) ⚡️
判断:5 < 6,是小数!✅
操作:
Prev往前走一步 -> 到索引 5 (此时arr[5]是大数 7)。交换
arr[Prev](7) 和arr[Cur](5)。
Cur继续走 -> 到索引 8。数组变身:
[6, 1, 2, 3, 4, 5, 9, 7, 10, 8]
8. Cur 遇到 10 (大) 🛑
判断:10 > 6。
操作:不做事。
Cur继续走 -> 到索引 9。
9. Cur 遇到 8 (大) 🛑
判断:8 > 6。
操作:不做事。
Cur继续走 -> 越界,循环结束。
终局:基准归位
此时:
Prev指向索引 5 (数值 5)。这是最后一个比 6 小的数。基准值
arr[0]是 6。最后一步:交换
arr[0](6) 和arr[Prev](5)。
最终结果:
[5, 1, 2, 3, 4, 6, 9, 7, 10, 8]
2.3.4代码实现
/*
int * a为待排序的数组
int left 为该数组的起始下标
int right 为该数组的末尾下标
*/
//前后指针法
int PartitionSlowFast(int* a,int left,int right)
{
//基准值的下标,默认为left
int keyi = left;
//定义慢指针
int prev = left ;
//定义快指针,寻找比a[keyi]小的元素
int cur = prev + 1;
//当快指针找到比a[keyi]小的元素,让慢指针++,交换a[cur]与a[prev]
while (cur<=right)
{
//当a[cur]找到小于基准值的数,prev进行改变
//prev==cur时不交换,因为此时prev与cur指向同一位置
if (a[cur] < a[keyi]&& ++prev != cur)
{
Swap(&a[cur], &a[prev]);
}
//cur指针一直向后移动
cur++;
}
Swap(&a[keyi],&a[prev]);
keyi = prev;
//返回基准值最后位置的下标
return keyi;
}
三、快速排序的实现
3.1快速排序实现
/*
int * a为待排序的数组
int left 为该数组的起始下标
int right 为该数组的末尾下标
*/
//分区的方式在于控制左右子数组的区间:
//[left,keyi-1] keyi [keyi+1, right]
void QuickSort(int* a, int left, int right)
{
//当数组只有一个元素或排序的区间不存在时退出
if (left >= right) return;
//方法一:hoare分区
//int keyi = PartionHoare(a, left, right);
//方法二:前后指针
//int keyi = PartitionSlowFast(a, left, right);
//方法三:挖坑法
int keyi =PartionDigHole(a, left, right);
//排序左数组
QuickSort(a, left, keyi - 1);
//排序右数组
QuickSort(a , keyi + 1, right);
}
3.2快速排序递归调用图

四、快速排序的优化
4.1三数取中
痛点:快速排序最怕什么?最怕基准值 (Pivot) 选得烂!
-
如果数组已经是倒序
[9, 8, 7, 6, ...],而你每次都傻傻地选第一个数做基准。 -
后果:每次切分都是 [1个元素,N-1元素],复杂度直接退化成 O(N^2),慢得像蜗牛!🐢
解决方案:不要只看第一个数,我们要“货比三家”!
我们在数组的 头部 (left)、中间 (mid)、尾部 (right) 三个位置上各取一个数,然后选出它们的中位数作为基准。
代码实现
int GetMidi(int a[],int left,int right)
{
int midi = left + (right - left) / 2;
//假设最小值下标为low,最大值下标为right
int low = left;
int high = right;
//a[low] <= a[midi]<= a[high]
if (a[low] > a[midi]) Swap(&low, &midi);
if (a[low] > a[high]) Swap(&low, &high);
if (a[midi] > a[high]) Swap(&midi, &high);
//返回中间值的下标:midi
return midi;
}
如下代码所示:将Hoare分区法进行优化,其余分区方法同理。
int PartionHoare(int *a,int left,int right)
{
//获得 数组a中 a[left] a[mid] a[right] 的中位数下标
int midi = GetMidi(a, left, right);
//为了不改变逻辑,仍旧将最左边的值作为基准值
//该处的值应改变为中位数,防止为极值
Swap(&a[left], &a[midi]);
int keyi = left;
//用begin指针从前往后找,right指针从后往前找
int begin = left, end = right;
while (begin < end)
{
//end从末尾向左找比a[keyi]小的元素
//保证begin<end
while (begin < end && a[end] >= a[keyi])
{
end--;
}
//begin从前往右找比a[keyi]大的元素
//保证begin<end
while (begin < end && a[begin] <= a[keyi])
{
begin++;
}
//交换当前a[begin] 和 a[end]
Swap(&a[begin], &a[end]);
}
//当begin 和 end 相遇时
//即begin==end
Swap(&a[keyi], &a[begin]);
keyi = begin;
return keyi;
}
4.2小区间优化
快速排序在数据量大时威力无穷,但当数据量很小(比如只剩 5 个、10 个元素)时,它的递归开销反而成了累赘。
-
递归需要压栈、出栈,这都是成本。
-
对于极短的数组,简单的插入排序 (Insertion Sort) 其实比快速排序更快!
解决方案:
当递归切分到的子数组长度小于某个阈值(通常是 10 到 15 左右)时,不再递归,直接用插入排序搞定它。
为什么选插入排序?
因为插入排序在“数据量小”或者“数据基本有序”的情况下,效率极高,且没有递归开销。
void QuickSort(int* a, int left, int right)
{
//当数组只有一个元素或排序的区间不存在时退出
if (left >= right) return;
//小区间优化
if (right - left + 1 < 10)
{
//进行插入排序
InsertSort(a + left, left - right + 1);
return;
}
//int keyi = PartionHoare(a, left, right);
//int keyi = PartitionSlowFast(a, left, right);
int keyi =PartionDigHole(a, left, right);
//排序左数组
QuickSort(a, left, keyi - 1);
//排序右数组
QuickSort(a , keyi + 1, right);
}
五、快速排序的复杂度
5.1最坏情况
基准值每次都选到极值(未优化时),导致每次分区域出现头重脚轻
n
/ \
n-1 0
/
n-2
/
...
/
1
1. 由于每趟进行分区需要用双指针遍历整个数组,故而一趟排序需要O(N)的时间复杂度
2. 最坏情况需要进行递归n层
3.故而时间复杂度最坏情况为O(N^2) 空间复杂度为O(n)。
5.2最好情况
每次分区都能完美平衡,即基准每次都选在中位数
n
/ \
n/2 n/2
/ \ / \
n/4 n/4 n/4 n/4
... ... ... ...
1. 由于每趟进行分区需要用双指针遍历整个数组,故而一趟排序需要O(N)的时间复杂度
2. 需要进行递归 log₂n 层
3.故而时间复杂度近乎为:O(n log n) 空间复杂度为 O(log n)。
5.3平均情况
由数学归纳法可以证明得到 :时间复杂度 O(n log n) 空间复杂度 O(log n)
既然看到这里了,不妨关注+点赞+收藏,感谢大家,若有问题请指正。









































 784
784

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








